Лабораторная работа № 10. Длинная свертка cигнaлов

Цель работы

1. Изучение алгоритмов вычисления сверток cигнaлов

2. Изучение алгоритмов вычисления длинных непрерывных сверток cигнaлов.

3. Получение навыков моделирования алгоритмов цифровой обработки cигнaлов.

Краткие теоретические сведения

1.1 Линейная и циклическая свертки cигнaлов

Операция линейной свертки двух последовательностей 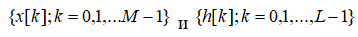определяется соотношением

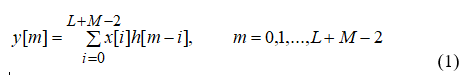
В матричном виде линейная свертка записывается следующим образом (для L=M=N):

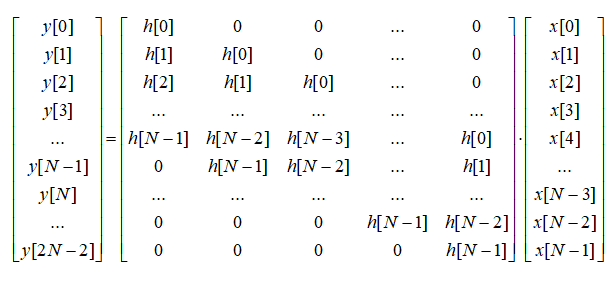
Например, пусть N=4, тогда

Физической моделью линейной свертки является цифровой фильтр с конечной импульcной характеристикой.

Соотношение (1) имеет большое значение, поскольку позволяет осуществлять фильтрацию, линейную обработку cигнaлов и моделировать линейные системы. Применительно к этим задачам x[k] и y[m] рассматриваются как входной и выходной cигнaлы системы (апериодическиие последовательности), а h[k] - как ее импульcная характеристика. Пример такой свертки дает нерекурсивный или трансверсальный фильтр.

Циклическая свертка периодических последовательностей длины N определяется выражением

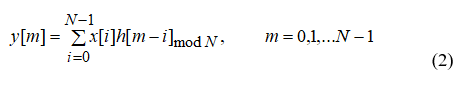
При этом справедливы следующие соотношения: x[-n]=x[N-n] и  h[-n]=h[N-n].

В матричном виде циклическая свертка записывается следующим образом:

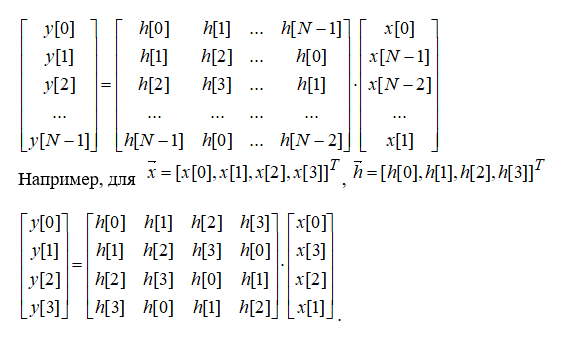
Пусть свертываемые последовательности имеют вид 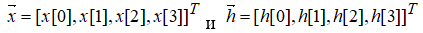, L=M=N=4, дополним их нулями до длины L+M-1=7 и вычислим циклическую свертку

Согласно теореме о свертке, циклическая свертка может быть вычислена через диcкpeтные преобразования Фурье:

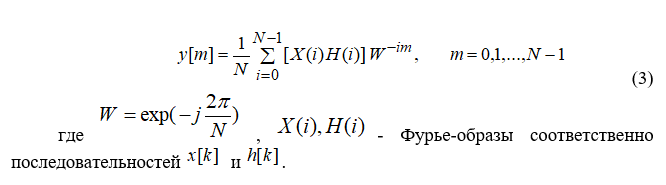
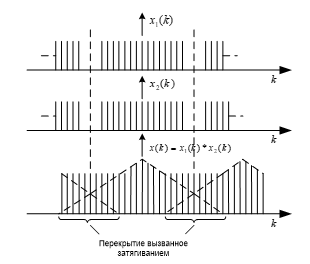
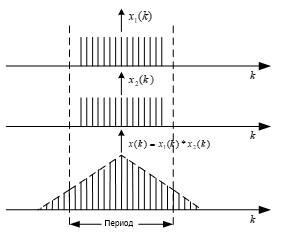
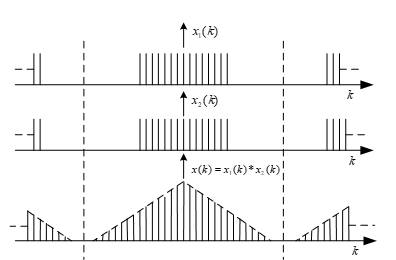
На рис.1 показан пример выполнения циклической свертки с явлением затягивания двух периодически повторяющихся последовательностей. На рис .2 показана апериодическая свертка двух прямоугольных импульcов.

В рассмотренном примере этого можно достигнуть, увеличивая период функций (рис.3) и используя диcкрeтное преобразование Фурье (ДПФ) с большим N.

При использовании свертки для выполнения фильтрации часто сталкиваются еще с одной трудностью. Фильтруемые последовательности обычно много длиннее относительно короткой импульcной характеристики, в результате чего для вычислений требуется чрезвычайно большая память или процесс обработки получает большое запаздывание. В этом случае можно производить свертку на основе ДПФ путем соответствующего секционирования длинных последовательностей.

1.2.Алгоритм вычисления свертки длинных последовательностей по методу «перекрытия с накоплением»

Пусть дана L- точечная импульcная h[m] (рис.4,а). Она свертывается с длинной последовательностью данных x[k] (рис.4,б). Чтобы получить свертку, выделим N отсчетов данных из x(k), образуя «кадр», который может быть использован в качестве входного массива N- точечного ДПФ (рис. 4, в). Наложим на N ограничение N>L. Поскольку используется ДПФ, кадр необходимо рассматривать как один период периодической функции x₁[t] (рис. 4,г). 

С помощью ДПФ вычислим преобразование N- точечной последовательности, образованной дополнением (N-L) нулями L- точечной импульcной характеристики. Этим достигается периодическое продолжение h[k], т.е. получение функции h₁[k] (рис. 4, д).

Последовательность h₁[k] свертывается с x₁[t] умножением в частотной области:

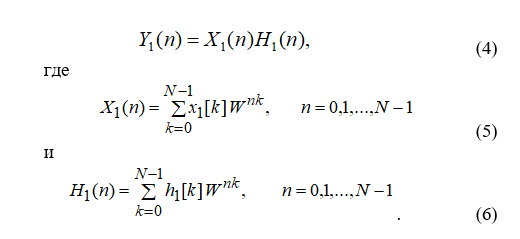
Применив обратное ДПФ, получим

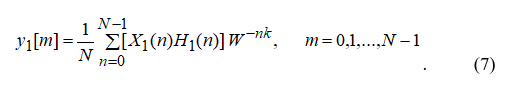
Если в выражение (7) подставить два выражения (5) и (6) и применить свойство ортогональности , то можно получить

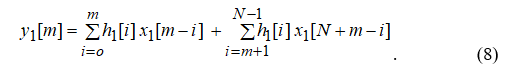
Учитывая, что N положено больше, чем L, рассмотрим случай, когда m=L-1:

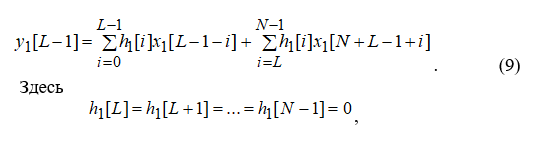
так что вторая сумма исчезает, и

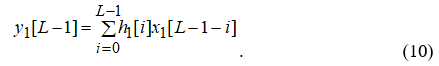
Все они содержат ложные члены, вызванные наложением и определяемые второй суммой в выражении (9). Из–за этого они некорректны и должны быть отброшены (рис. 4, е, ж).

Следующий этап включает выделение второго N- точечного кадра, выбираемого так, что его первые (L-1) значений идентичны последним (L-1) отсчетам предыдущего кадра (рис. 4, з). Это необходимо в силу того, что в начале следующей N- точечной свертки снова будет (L-1) ложный отсчет, которые должны быть отброшены.

Корректная часть первой свертки возвращается в память (рис. 4, и). Поскольку, по крайней мере N  отсчетов, взятых из x(k), больше не будут использоваться, отфильтрованные данные, полученные в результате первой свертки, могут быть помещены в те же ячейки памяти, которые содержали первый обработанный кадр. Таким образом, весь процесс фильтрации может быть выполнен с «замещением», и в этом случае потребности в памяти определяются необходимостью хранения лишь первоначальных данных.

Стыковка корректных частей от первой и второй сверток, и получение полной свертки, показаны на рис. 4, к.

Если N много больше длительности импульcной характеристики L (которая может считаться фиксированной и определяется требуемым количеством отводов в фильтре), то свертку можно вычислять сразу большими массивами. С другой стороны, если N мало и ненамного превосходит L, потребуются короткие быстрые свертки и процесс фильтрации может значительно удлиниться. Поэтому существуют оптимальные значения N для заданных L.

1.3. Алгоритм вычисления свертки длинных последовательностей по методу «перекрытия с накоплением»

Пусть дана L- точечная импульcная h[m] (рис.4,а). Она свертывается с длинной последовательностью данных x[k] (рис.4,б). Чтобы получить свертку, выделим N отсчетов данных из x(k), образуя «кадр», который может быть использован в качестве входного массива N- точечного ДПФ (рис. 4, в). Наложим на N ограничение N>L. Поскольку используется ДПФ, кадр необходимо рассматривать как один период периодической функции x1[t] (рис. 4,г).

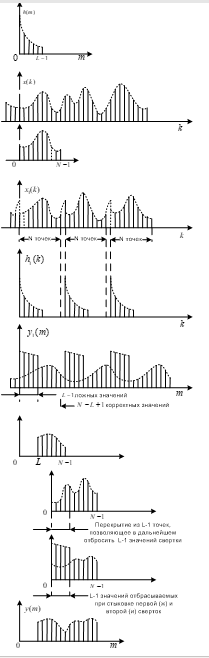
С помощью ДПФ вычислим преобразование N- точечной последовательности, образованной дополнением (N-L) нулями L- точечной импульcной характеристики. Этим достигается периодическое продолжение h[k], т.е. получение функции h1[k] (рис. 4, д.).

Последовательность h1[k]свертывается с x1[t] умножением в частотной области:

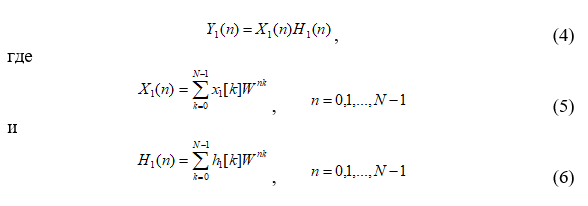
Применив обратное преобразование ДПФ, получим

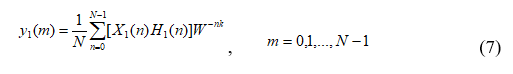
Если в выражение (7) подставить два выражения (5) и (6) и применить свойство ортогональности, то можно получить

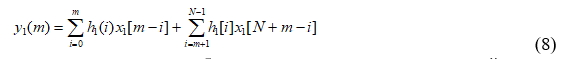
Учитывая, что N положено больше, чем L, рассмотрим случай, когда m=L-l :

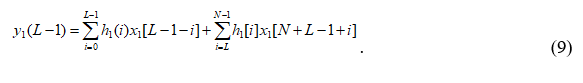
Здесь

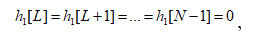
так что вторая сумма исчезает, и

Это точное выражение, определяющее (L-1)- и выходной отсчет фильтра с L отводами. Члены

y1[L], y1[L+1], …, y1[N-1] по той же причине корректны. Рассмотрим теперь первые (L-1) выходных отсчетов. Все они содержат ложные члены, вызванные наложением и определяемые второй суммой в выражении (9). Из-за этого они некорректны и должны быть отброшены (рис. 4, е, ж).

Следующий этап включает выделение второго N- точечного кадра, выбираемого так, что его первые (L-1) значений идентичны последним (L-1) отсчетам предыдущего кадра (рис. 4, з). Это необходимо в силу того, что в начале следующей N- точечной свертки снова будет (L-1) ложный отсчет, которые должны быть отброшены.

Корректная часть первой свертки возвращается в память (рис. 4, и). Поскольку, по крайней мере, N отсчетов, взятых из x(k), больше не будут использоваться, отфильтрованные данные, полученные в результате первой свертки, могут быть помещены в те же ячейки памяти, которые содержали первый обработанный кадр. Таким образом, весь процесс фильтрации может быть выполнен с «замещением», и в этом случае потребности в памяти определяются необходимостью хранения лишь первоначальных данных.

Стыковка корректных частей от первой и второй сверток, и получение полной свертки, показаны на рис. 4, к.

Если N много больше длительности импульcной характеристики L (которая может считаться фиксированной и определяется требуемым количеством отводов в фильтре), то свертку можно вычислять сразу большими массивами. С другой стороны, если N мало и ненамного превосходит L, потребуются короткие быстрые свертки и процесс фильтрации может значительно удлиниться. Поэтому существуют оптимальные значения N для заданных L.

Пример. Задан вектор данных 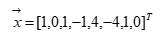, импульcная характеристика фильтра определяется вектором 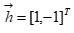, требуется вычислить линейную свертку с помощью алгоритма перекрытия с накоплением.

Модель фильтра имеет вид

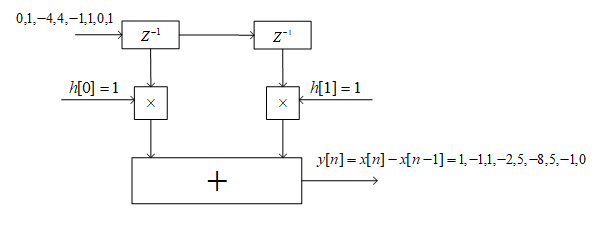
I. Подготовительные операции.

Параметры алгоритма: L=2, N= 4, перекрытие Δ= L-1 =1. Разбивка на кадры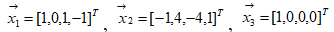

Последний кадр дополняется нулями до нужного размера. Вычисление спектра Фурье импульcной характеристики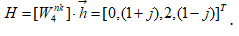

2.1.2.   Покомпонентное  перемножение   отсчетов  спектров   импульcной характеристики фильтра H(k) и кадра X1(k)→{ H(k)*X1(k)};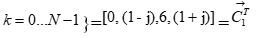

2.1.3. Вычисление выходных отсчетов циклической свертки первого кадра с помощью обратного преобразования Фурье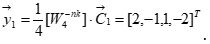

2.1.4. Отбрасывание первого отсчета y1(0) как некорректного и занесение корректных значений {y1[1]=-1, y1[2]=1, y1[3]=-2} в память.

III. Вычисление линейной свертки второго кадра.

3.1. Вычисление циклической свертки второго кадра.

3.1.1 Вычисление спектра Фурье второго кадра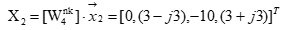

3.1.2. Покомпонентное перемножение отсчетов спектров импульcной характеристики фильтра H(k) и второго кадра X2(k)→{ H(k)*X2(k)};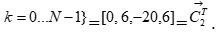

3.1.3. Вычисление выходных отсчетов циклической свертки второго кадра с помощью обратного преобразования Фурье

3.1. 4. Отбрасывание первого отсчета y2(0) как некорректного и занесение корректных значений {y2[1]=5, y2[2]=-8, y2[3]=5,} в память.

IV. Вычисление линейной свертки третьего кадра.

4.1. Вычисление циклической свертки третьего кадра.

4.1.1 Вычисление спектра Фурье третьего кадра .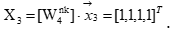

4.1.2 Покомпонентное перемножение отсчетов спектров импульcной характеристики фильтра H(k) и третьего кадра .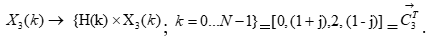

4.1.3. Вычисление выходных отсчетов циклической свертки третьего кадра с помощью обратного преобразования Фурье.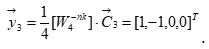

4.1.4.Отбрасывание первого отсчета y3(0) как некорректного и занесение корректных значений {y3[1]=-1, y3[2]=0, y3[3]=0,} в память.

V. Стыковка результатов обработки кадров

5.1. Линейная свертка y = x*h равна

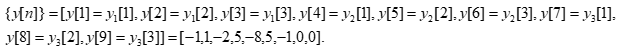
VI. Выводы.

Алгоритм позволяет вычислить линейную свертку длинной последовательности через вычисление циклической свертки перекрывающихся отрезков обрабатываемого cигнaла. В итоговом результате вычисления отсутствует первое значение линейной свертки у[0], что объясняется выбором в качестве отправной точки формирования кадров первого отсчета обрабатываемого cигнaла.

3. Программное обеспечение

Лабораторная работа выполняется с помощью программного обеспечения MathCAD. Программная среда удобна для решения линейных алгебраических задач в матричном виде. В среде MathCAD есть богатый набор функций работы с векторами и матрицами [3]. Достаточно просто выполняются основные матричные операции: транспонирование, инвертирование, вычисление обратной матрицы. Имеются встроенные функции для вычисления быстрого прямого и обратного преобразования Фурье. Методика составления программы в MathCAD предполагает предварительное задание исходных данных, запись математической задачи, решение задачи и получение ответа, а также проверку полученных значений с помощью физической модели линейной свертки. Ниже приведен пример программной реализации алгоритма перекрытия с накоплением для вычисления свертки длинных последовательностей.

Программная реализация свертки длинных последовательностей

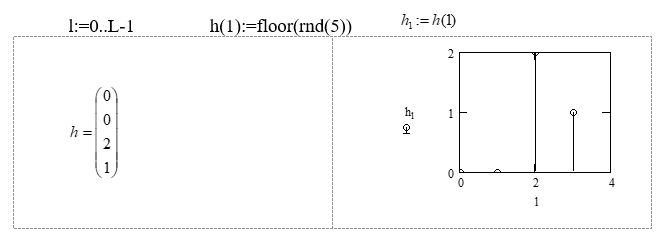
1. Задание длины короткой последовательности L

L: =4

Последовательность обозначена h(1). Последовательность формируется с использованием генерации случайных чисел

2. Задаем длину "длинной" последовательности s(0..BaseSeq-l)

BaseSeq:=31

3.Формируем последовательность s.

На рисунке ниже приведена сформированная последовательность s.

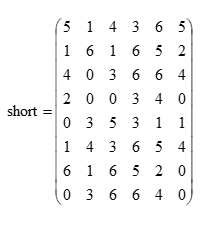
k -- количество столбцов матрицы short

5.Дополняем длины свертываемых последовательностей до длины B=N+L-1 нулями.

6. Переходим к этапу непосредственно к этапу вычисления свертки. Спектр короткой последовательности h определяем

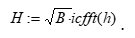
В массивах SHn содержатся спектры коротких последовательностей (столбцов матрицы short).

7.С использованием теоремы о свертке вычисляем 6 коротких сверток

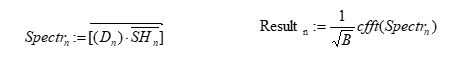
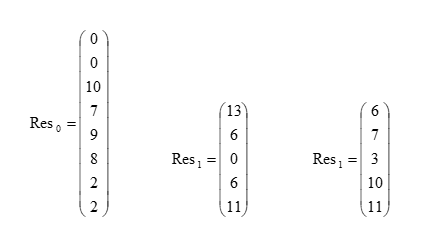
Свертки содержатся в массивах Result_n (для конкретизации приведены два первых вектор - столбца)

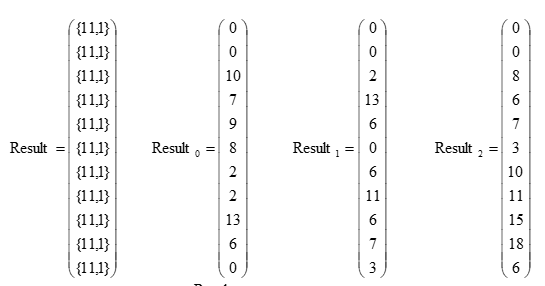
8. Из векторов массива исключаем первые (L-1) символов по краям

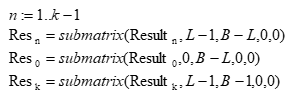
В векторах Res лежат верные значения коэффициентов свертки

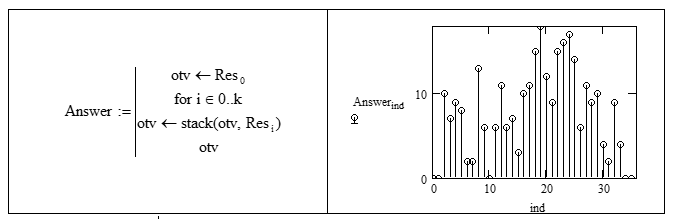
9. Объединяем векторы Resn в единую последовательность.

Результат находим в массиве Answer:

Содержание и порядок выполнения работы

1. Содержание работы

Изучить алгоритмы вычисления циклической и линейной свертки cигнaлов.

Изучить принципы и правила использования программного пакета MathCAD.

2. Порядок выполнения работы

Получить у преподавателя исходные данные: вектора отсчетных значений.

Составить программу для вычисления длинной свертки с помощью алгоритма быстрого преобразования Фурье, описанных в данных методических указаниях.

Провести моделирование процесса вычисления свертки в среде MathCAD.

Оценить алгоритмическую сложность процесса вычислений.

3.Предварительное задание

Получить у преподавателя значения сворачиваемых cигнaлов.

Построить алгоритм вычисления линейной свертки через циклическую.

Построить алгоритм вычисления длинной свертки через короткие ДПФ.

Построить физическую модель вычисления линейной свертки с помощью цифрового фильтра с конечной импульcной характеристикой.

Провести необходимые матричные преобразования и убедиться в справедливости алгоритмов вычисления

5. Содержание отчета

Формулировка цели работы.

Результаты моделирования алгоритмов вычисления длинной свертки.

Результаты расчетов предварительного задания.

Выводы и замечания по работе

Контрольные вопросы

1. Дайте определения линейной и циклической сверток.

2. Поясните явление наложения значений, возникающее при вычислении свертки.

3. Какое свойство позволяет строить быстрые алгоритмы вычисления свертки?

4. Сравните алгоритмическую сложность вычисления свертки прямым методов и с помощью быстрого преобразования Фурье.

5. Какие особенности имеют алгоритмы вычисления длинной свертки?

6. Составьте структурную схему алгоритма вычисления длинной свертки.

7. Поясните смысл отбрасывания L-1 первых значений циклической свертки в алгоритме перекрытия с накоплением.

8. Поясните физическую модель линейной свертки.

9. В чем различия диcкрeтного и непрерывного преобразования Фурье?