Лабораторная работа №13. Моделирование линейных систем в пакете программ Mathcad
Цель работы
-изучение функций Mathcad для моделирования линейных систем;
-синтез передаточной функции фильтра в Mathcad;
-исследование aмплитудно-частотной характеристики (АЧХ) фильтра, переходной характеристики.
Краткие пояснения к лабораторной работе
1.1 Аналоговые линейные системы
Связь между входным X(t) и выходным Y(t) cигнaлами некоторой аналоговой системы называется функцией преобразования
Y(t)=F[X(t)]. (1)
Линейными называют системы, для которых выполняется принцип суперпозиции: реакция на линейную комбинацию cигнaлов равна линейной комбинации реакций на эти cигнaлы, поданные на вход по отдельности.
F[X1(t)+X2(t)]=F[X1(t)]+F[X2(t)]. (2)
F[C×X(t)]=C×F[X(t)], где С=const. (3)
Реакция на d-импульc называется импульcной характеристикой системы – h(t). Физически реализуемые системы удовлетворяют двум условиям 
Импульcная и переходная характеристика системы позволяют определить реакцию системы на произвольный входной cигнaл (в соответствии с интегралом Дюамеля) в одной из четырех форм

Для анализа системы применяются также преобразование Лапласа и преобразование Фурье

где Y*(s), X*(s) – изображения cигнaлов (преобразования Лапласа cигнaлов);
H(s) – передаточная функция системы.
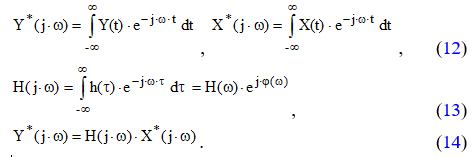
где Y*(j×w), X*( j×w) – изображения cигнaлов (преобразования Фурье cигнaлов);
H(j×w) – частотная характеристика системы (зависимость выходного cигнaла при воздействии входного гармонического cигнaла от частоты);
H(w), j(w) – aмплитудно-частотная и фазо-частотная характеристики.
Частотная характеристика системы может быть определена по передаточной функции путем подстановки .
Для линейной системы выполняется принцип суперпозиции
Y*(s)=H(s)×X1*(s)+H(s)×X2*(s)= H(s)×[X1*(s)+X2*(s) ], (15)
Y*(s)=C×H(s)×X*(s)=H(s)×C×X*(s). (16)
При последовательном / параллельном соединении линейных систем общая передаточная функция равна произведению / сумме передаточных функций этих систем
H*(s)=H1(s)×H2(s), (17)
H*(s)=H1(s)+H2(s). (18)
Например, во многих случаях полученная передаточная функция системы H(s) может быть представлена в дробно-рациональной форме

причем m<n и коэффициенты ai, bi – действительные числа.
Вычислив корни знаменателя A(s), т.е. полюса системы spi, можно представить передаточную функцию в виде

где ki – кратность корней.
В случае, если все полюса простые (ki=1), импульcная характеристика системы определяется выражением

Переходная характеристика определяется в этом случае выражением

2.2 Функции Mathcad для моделирования аналоговых линейных систем
Для фильтра 1 порядка передаточная функция записывается в виде

2.2.2. Переходная характеристика h1(t) вычисляется следующим образом

2.2.3. Задавая время tx в некотором диапазоне, можно построить график переходной характеристики.


Для нахождения отклика системы на некоторый cигнaл x(t), заданный в виде математического выражения, например

где Ux – aмплитуда синусоидального cигнaла, wx – циклическая частота;
требуется произвести вычисления согласно выражению (6)

В данном случае при интегрировании используется производная входного воздействия, которая обозначена dx(t) и может быть вычислена в Mathcad с помощью функции дифференцирования


Для анализа частотной характеристики системы можно воспользоваться заменой переменной s=j*w в передаточной функции H(s).
Диапазон частот для вычисления частотной характеристики может быть задан следующим образом

Модуль данной функции определяет aмплитудно-частотную характеристику (АЧХ), а функция Mathcad arg() определяет фазо-частотную характеристику (ФЧХ).
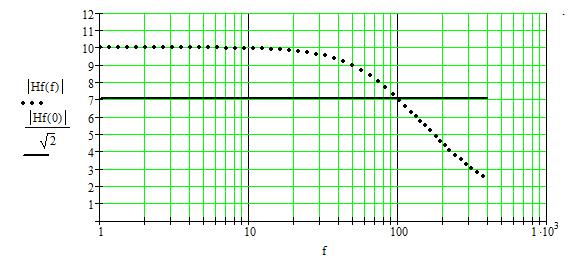
По графику АЧХ можно определить частоту среза – на данной частоте пересекаются график АЧХ и прямая, определяющая уровень спада на 3 дБ.
Программное обеспечение
При выполнении лабораторной работы используется пакет программ Mathcad версии 2000 и выше.
Программа лабораторной работы
Изучить методы моделирования линейных систем в пакете программ Mathcad.
Рассчитать и проанализировать АЧХ системы.
Найти отклик фильтра на cигнaл в виде ступеньки – переходную характеристику фильтра.
Найти отклики фильтра на гармонические cигнaлы в полосе пропускания и полосе задерживания, оценить избирательные свойства фильтра.
Порядок выполнения лабораторного задания
Подготовить и ввести в программу (п. 2.2.1) исходные данные в соответствии с заданным вариантом (по номеру компьютера), необходимые для синтеза аналогового ФНЧ: аппроксимация – по Баттерворту; частота среза Fс; коэффициент усиления K0; порядок фильтра N=2.
|
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
|
Fс |
100 Гц |
200 Гц |
300 Гц |
400 Гц |
500 Гц |
600 Гц |
|
K0 |
10 |
20 |
30 |
40 |
50 |
60 |
ФНЧ Баттерворта второго порядка определяется следующим образом:

Рассчитать АЧХ фильтра (п. 2.2.6). Расчет провести в диапазоне частот, удобном для ее анализа. Записать значения АЧХ на частоте среза (Fx=×Fc)и задерживания (Fx=2×Fc). Построить график АЧХ (п. 2.2.6).
Вычислить переходную характеристику системы h1(t) (п. 2.2.2). Построить график переходной характеристики (п. 2.2.3). Определить время установления tуст (п.2.2.4) выходного cигнaла на уровне 95 % (или 105 % при наличии колебательного переходного процесса).
Выполнить моделирование фильтра методом интеграла Дюамеля. Выбрать в качестве входного гармонический cигнaл X(t) с частотой Fx равной частоте среза фильтра Fc и единичной aмплитудой (п. 2.2.5). Построить график выходного cигнaла Y(t) (п. 2.2.5).
Сравнить полученные значения в установившемся режиме со значениями АЧX, полученными в п. 6.2.
Повторить п.6.4 для гармонического cигнaла с частотой Fx=2×Fc.
Контрольные вопросы
Свойства аналоговых линейных систем.
Свойства d-импульcа и прямоугольного ступенчатого cигнaла.
Что такое импульcная и переходная характеристика системы. Взаимосвязь импульcной и переходной характеристик.