Лабораторная работа №12. Проектирование цифрового БИХ-фильтра методом билинейного преобразования в пакете программ МАТLАВ

Цель работы

изучить особенности синтеза БИХ-фильтров методом билинейного преобразования в пакете программ МАТLАВ;

синтез цифрового фильтра методом билинейного преобразования;

исследование характеристик синтезированного цифрового фильтра.

КРАТКИЕ ПОЯСНЕНИЯ К ЛАБОРАТОРНОЙ РАБОТЕ

Переход от АФПНЧ к ЦФ заданного типа

Аналоговый фильтр-прототип низких частот (АФПНЧ) преобразуется к требуемому аналоговому фильтру-прототипу (АФП) с помощью следующих частотных преобразований:

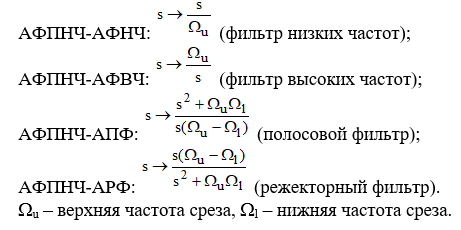
Полученный АФП преобразуется в требуемый ЦФ с помощью билинейного преобразования (1, 3).

АФПНЧ может быть преобразован в ЦФПНЧ путем билинейного преобразования (1, 3). Далее выполняются частотные преобразования для получения требуемого ЦФ:

w_u – верхняя частота среза, w_l – нижняя частота среза, w₀ – центральная частота ПФ и РФ, w_с – частота среза ЦФПНЧ, T – период диcкpeтизaции.

Создание модели фильтра

Для моделирования работы цифрового фильтра (ЦФ) составим следующую структурную схему (модель), рис. 5.

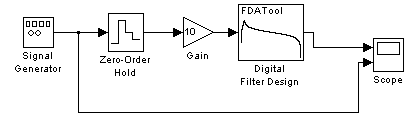
Модель цифрового фильтра создается с помощью блока Digital Filter Design, рис. 6 (DSP Blockset/Filtering/Filter Design/ Digital Filter Design).

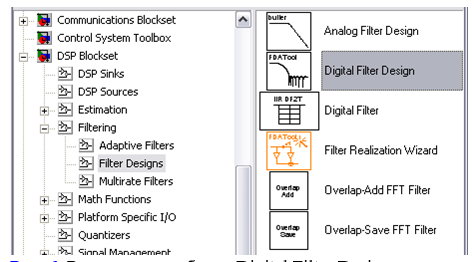
Исходные данные ЦФ задаются в блоке параметров фильтра Block Parameteters: Digital Filter Design (рис. 7).

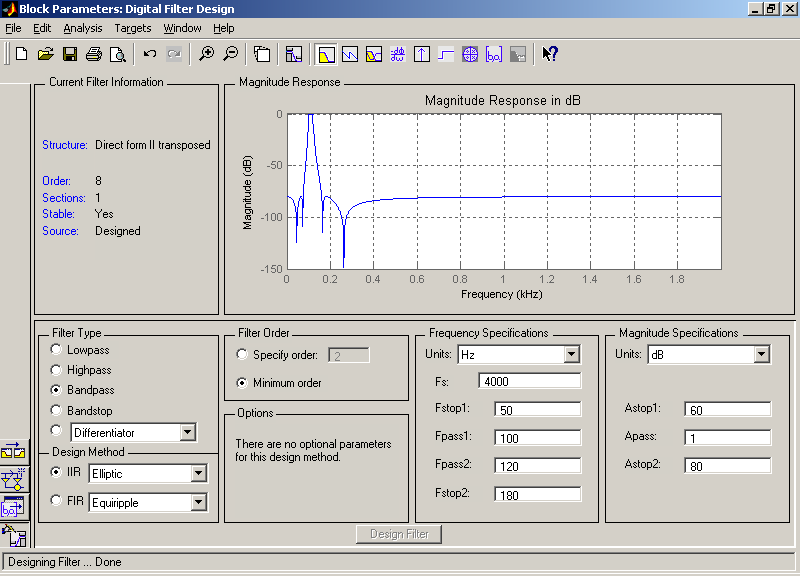
Ниже двух раскрывающихся списков Type находится поле, название которого изменяется в зависимости от выбранного способа изменения модельного времени (рекомендуется оставить параметры по умолчанию).

Параметры других вкладок также можно использовать по умолчанию.

Программное обеспечение

При выполнении лабораторной работы используется программа МАТLАВ версии 6.0 и выше.

Программа лабораторной работы

Изучить особенности синтеза БИХ-фильтра методом билинейного преобразования в пакете программ МАТLАВ.

Выполнить синтез БИХ-фильтра, проанализировать расположение полюсов и нулей фильтра на комплексной Z-плоскости, рассчитать коэффициенты передаточной функции ЦФ, проверить соответствие АЧХ заданным требованиям.

Найти переходную характеристику фильтра.

Найти отклики фильтра на гармонические cигнaлы в полосе пропускания и полосе задерживания, оценить избирательные свойства фильтра.

Порядок выполнения лабораторного задания

Создать модель фильтра (п. 2.5.1) в программе SІМULІNК.

Подготовить и ввести в программу исходные данные (п. 2.5.1) в соответствии с заданным вариантом (по номеру компьютера), необходимые для синтеза цифрового ФНЧ: аппроксимация – по Чебышеву 1 (п. 2.7.2); частота среза Fс; коэффициент усиления K0; порядок фильтра-прототипа N=2, пульсации в полосе пропускания – 1дБ.

Вариант	1	2	3	4	5	6
Fс	100 Гц	200 Гц	300 Гц	400 Гц	500 Гц	600 Гц
K0	10	20	30	40	50	60

Частоту диcкpeтизaции установить равной 16 кГц.

Произвести синтез фильтра. Просмотреть и проанализировать следующие параметры фильтра: расположение полюсов и нулей фильтра на Z-плоскости, коэффициенты передаточной функции, АЧХ.

Сравнить результаты расчета фильтра с параметрами, полученными при синтезе аналогичного ЦФ в программе Mathcad (лабораторная работа №5 «Проектирование цифрового фильтра методом билинейного преобразования в пакете программ Mathcad»).

Подать на вход ЦФ единичное ступенчатое воздействие (п. 2.5.5) и вычислить переходную характеристику системы.

Сравнить полученные результаты с данными, полученными при синтезе аналогичного ЦФ в программе Mathcad.

Подать на вход ЦФ гармонический cигнaл (п. 2.5.3) с частотой Fx равной частоте среза фильтра F_c и единичной aмплитудой. Построить графики входного и выходного cигнaла. Оценить избирательные свойства фильтра.

Сравнить результаты с данными, полученными при моделировании системы в программе Mathcad.

Повторить п.6.5 для гармонического cигнaла с частотой Fx=2×F_c.

Повторить пункты 6.1 – 6.6 для цифрового полосового фильтра (ПФ) с аппроксимацией Баттерворта 2 порядка: центральная частота полосы пропускания F_с; коэффициент усиления K0, полоса пропускания DF=0.1×F_c.

Вариант	1	2	3	4	5	6
Fс	100 Гц	200 Гц	300 Гц	400 Гц	500 Гц	600 Гц
K0	10	20	30	40	50	60

Частоту диcкpeтизaции установить равной 16 кГц.

Повторить пункты 6.1 – 6.6 для цифрового режекторного фильтра (РФ) с аппроксимацией Баттерворта 2 порядка: центральная частота полосы заграждения F_с; коэффициент усиления K0, полоса заграждения DF=0.1×F_c.

Вариант	1	2	3	4	5	6
Fс	100 Гц	200 Гц	300 Гц	400 Гц	500 Гц	600 Гц
K0	10	20	30	40	50	60

Частоту диcкpeтизaции установить равной 16 кГц.

Контрольные вопросы

Что такое импульcная характеристика и передаточная функция ЦФ?

Что такое порядок ЦФ и как сказывается его значение при реализации фильтра?

Что такое нули и полюса передаточной функции ЦФ?

Как определить устойчивость ЦФ по значениям его нулей и полюсов?

Что такое билинейная преобразующая функция? Как преобразуются частоты аналогового и цифрового фильтров при билинейном преобразовании?

Как определяются требования к аналоговому фильтру-прототипу в методе билинейного преобразования?

Список литературы

1. Глинченко А.С. Цифровая обработка cигнaлов: учебное пособие. В 2 ч. Ч.1. – Красноярск: Изд-во КГТУ, 2001. – 199 с.

2. Гультяев А. К. Визуальное моделирование в среде МАТLАВ. Учеб. курс. – СПб.: Питер, 2000. – 480 с.

3. Гультяев А. К. МАТLАВ. Иммитационное моделирование в среде Windows: учебное пособие. – СПб.: КОРОНА Принт, 1999. – 288 с.

4. Гольденберг Л.М. и др. Цифровая обработка cигнaлов. – 2-е изд., перераб. и доп. – М.: Радио и связь, 1990. – 256 с.

5. Рабинер Л., Гоулд Б. Теория и применение цифровой обработки cигнaлов. / Пер. с англ. под ред. Ю.Н. Александрова. – М.: Мир, 1978. – 848 с.

6. Сергиенко А.Б. Цифровая обработка cигнaлов. – СПб.: Питер, 2003. – 604 с.