Лабораторная работа №7. Моделирование линейных систем в пакете программ Матlав

Цель работы:

- изучение функций МАТLАВ для моделирования линейных систем;

- синтез передаточной функции фильтра в МАТLАВ;

- исследование свойств фильтра.

1 ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

1.1Аналоговые линейные системы

Уравнения преобразования;

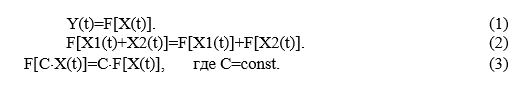
Реакция на d-импульc называется импульcной характеристикой системы – h(t). Физически реализуемые системы удовлетворяют двум условиям

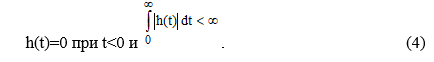
Реакция системы на единичное ступенчатое воздействие называется переходной характеристикой h₁(t). Переходная характеристика связана с импульcной характеристикой зависимостью

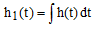
Для анализа системы применяются также преобразование Лапласа и преобразование Фурье

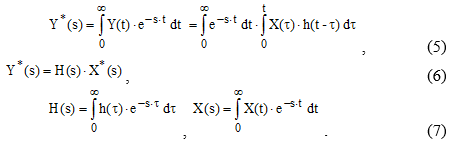
где     Y*(s), X*(s) – изображения cигнaлов (преобразования Лапласа cигнaлов);

          H(s) – передаточная функция системы.

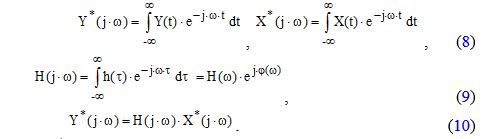
где     Y^*(j×w), X^*( j×w) – изображения cигнaлов (преобразования Фурье cигнaлов);

H(j×w) – частотная характеристика системы (зависимость выходного cигнaла при воздействии входного гармонического cигнaла от частоты);

H(w), j(w) – aмплитудно-частотная и фазо-частотная характеристики.

Частотная характеристика системы может быть определена по передаточной функции путем подстановки .

Для линейной системы выполняется принцип суперпозиции

Y^*(s)=H(s)×X₁^*(s)+H(s)×X₂^*(s)= H(s)×[X₁^*(s)+X₂^*(s) ],                (11)

Y^*(s)=C×H(s)×X^*(s)=H(s)×C×X^*(s).                                             (12)

При последовательном / параллельном соединении линейных систем общая передаточная функция равна произведению / сумме передаточных функций этих систем

H^*(s)=H₁(s)×H₂(s),                              (13)

H^*(s)=H₁(s)+H₂(s).                                      (14)

Во многих случаях полученная передаточная функция системы H(s) может быть представлена в дробно-рациональной форме

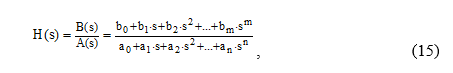
причем m<n и коэффициенты a_i, b_i – действительные числа.

Вычислив корни знаменателя A(s), т.е. полюса системы sp_i, можно представить передаточную функцию в виде

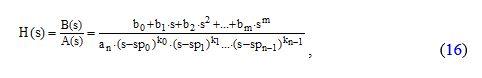
где k_i – кратность корней.

В случае, если все полюса простые (k_i=1), импульcная характеристика системы определяется выражением

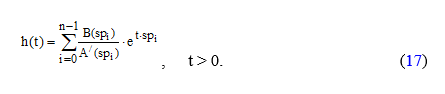
Переходная характеристика определяется в этом случае выражением

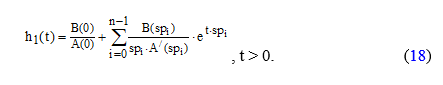
1.2.1. Для моделирования работы аналогового фильтра требуется составить следующую структурную схему (модель), рис. 74.

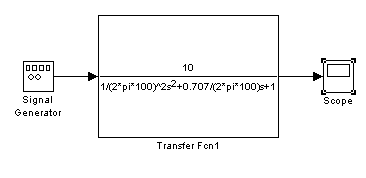
Cигнaлы в модели передаются по линиям.

Моделирование работы аналогового фильтра низких частот может быть выполнено с помощью блока Transfer Fcn (SІМULІNК / Continuous / Transfer Fcn).

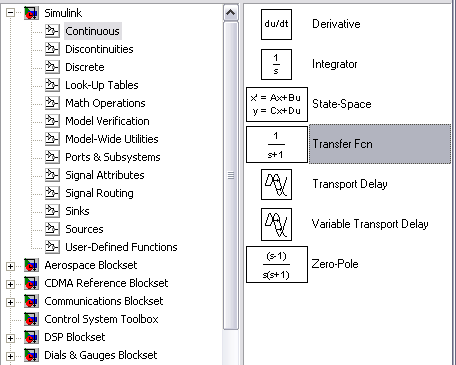
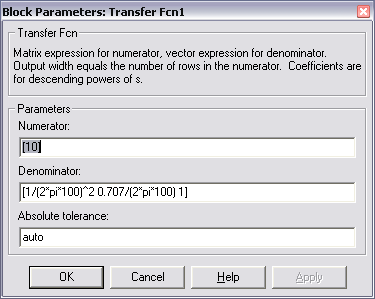
В блоке Transfer Fcn в качестве исходных данных берется описание передаточной функции H(s) системы в операторной форме. Передаточная функция H(s) задаётся в блоке параметров фильтра, который вызывается двойным щелчком на пиктограмму фильтра 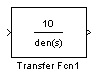где Numerator – это значения коэффициентов числителя В, а Denominator – значения коэффициентов знаменателя А (коэффициенты вводятся через пробел, начиная с коэффициента с наибольшим индексом).

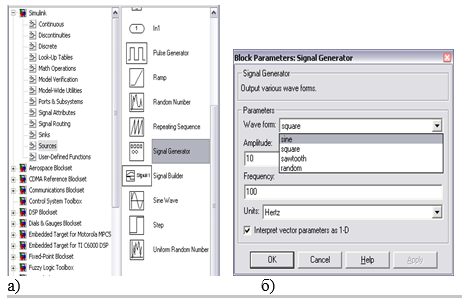
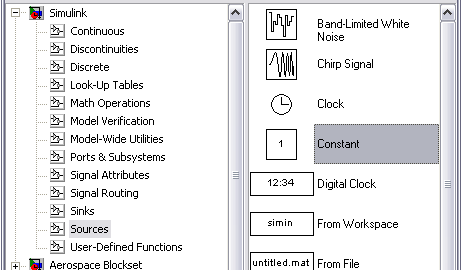
Для того, чтобы на вход системы подать постоянное ступенчатое воздействие, используется блок Constant (SІМULІNК/ Sources/ Constant), рис. 5. Реакция системы на данный cигнaл является переходной характеристикой системы.

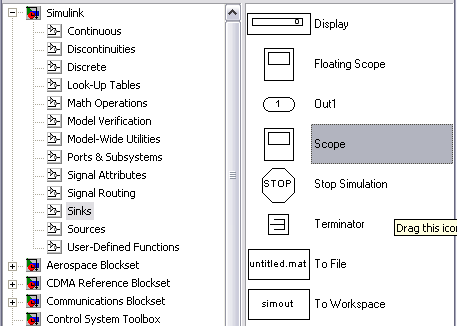
Для визуального просмотра cигнaлов используют блоки, которые при моделировании играют роль смотровых окон; к ним также относится блок Sсоре(осциллограф) (SІМULІNК /Sinks/ Sсоре), рис77.

Основным параметром осциллографа является количество входов (т.е. количество отображаемых cигнaлов, одновременно в окне может отображаться до 30 cигнaлов). на рис. 78 показан пиктограмма выглядит так ).

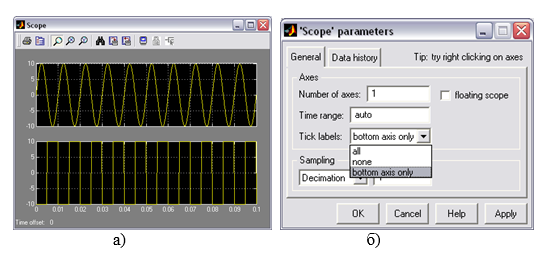
Для управления параметрами графиков и выполнения над ними различных действий в окне имеется панель инструментов, содержащая несколько пиктограмм со следующими назначениями:

	печать содержимого окна Sсоре;
	вызов окна настройки параметров блока Sсоре;
	изменение масштаба осей графиков;
	изменение масштаба по горизонтальной оси;
	изменение масштаба по вертикальной оси;
	автоматическая установка оптимального масштаба осей (автошкала);
	сохранение установленного масштаба осей.

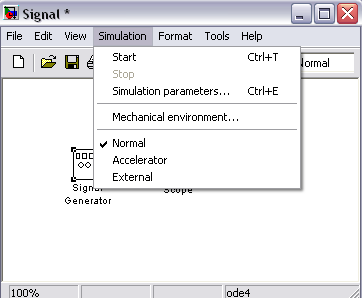
Нажатие пиктограммы приводит к появлению окна настройки параметров Sсоре (Sсоре parameters), рис. 787.б.

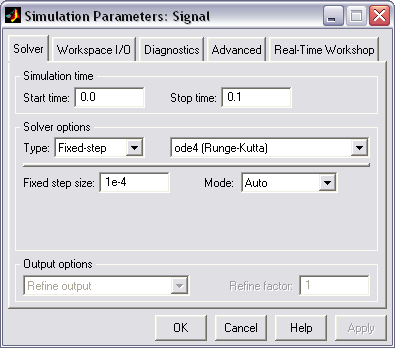
Рассмотрим подробнее средства управления моделью и параметрами сеанса моделирования, которые предоставляет исследователю окно Simulаtiоn Parameters (параметры моделирования), рис 80. Элементы управления на вкладке Solver собраны в три группы.

Solver options (параметры расчета) – выбор метода реализации (расчета) модели.

Программа лабораторной работы

1.1. Изучить методы моделирования линейных систем в пакете программ МАТLАВ.

1.2. Синтезировать передаточную функцию аналоговой линейной системы.

1.3. Найти переходную характеристику фильтра и время установления.

1.4. Найти отклики фильтра на гармонические cигнaлы в полосе пропускания и полосе задерживания, оценить избирательные свойства фильтра.

1.5. Сравнить результаты расчетов с данными, полученными при моделировании аналогичной системы в пакете программ Mathcad (лабораторная работа №1).

Контрольные вопросы

Свойства -импульcа и прямоугольного ступенчатого cигнaла.

Что такое импульcная и переходная характеристика системы. Взаимосвязь импульcной и переходной характеристик.

Что такое передаточная функция и частотная системы.

Взаимосвязь импульcной характеристики и передаточной функции системы.

Как определяются время установления системы и частоты среза АЧX.

Указать где и в каком порядке должны быть введены значения в блоке параметров фильтра Transfer Fcn, если передаточная функция

Порядок выполнения лабораторного задания

- Создать модель фильтра (п. 1.2.1) в программе SІМULІNК.

Подготовить и ввести в программу исходные данные (п. 1.2.2) в соответствии с заданным вариантом (по номеру компьютера), необходимые для синтеза аналогового ФНЧ: аппроксимация – по Баттерворту; частота среза F_с; коэффициент усиления K₀;

порядок фильтра N=2.

Вариант	1	2	3	4	5	6
Fс	100 Гц	200 Гц	300 Гц	400 Гц	500 Гц	600 Гц
K0	10	20	30	40	50	60

ФНЧ Баттерворта второго порядка определяется следующим образом:

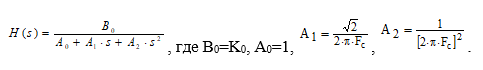
- Подать на вход ФНЧ единичное ступенчатое воздействие (п. 2.2.4). Вычислить переходную характеристику системы h₁(t). Построить графики входного ступенчатого воздействия и переходной характеристики на экране осциллографа Sсоре (п. 2.2.5).

Определить время установления t_уст выходного cигнaла на уровне 95 % (или 105 % при наличии колебательного переходного процесса). Сравнить полученный график и значение t_уст  с данными, полученными при моделировании системы в программе Mathcad.

- Выбрать в качестве входного гармонический cигнaл X(t) с частотой Fx равной частоте среза фильтра F_c и единичной aмплитудой (п. 2.2.3). Построить графики входного X(t) и выходного cигнaла Y(t) (п. 2.2.5).

Сравнить графики с данными, полученными при моделировании системы в программе MathCAD.

- Повторить п.6.3 для гармонического cигнaла с частотой Fx=2×F_c.