Лабораторная работа №8. Компьютерное моделирование и обработка нестационарных cигнaлов

Цель работы: Изучить основы ОЦОС

Теоретические сведения

Цифровая обработка cигнaлов в сложных радиоэлектронных cиcтемaх характеризуются рядом особенностей, осложняющих решение радиотехнических задач.

В качестве фильтра в структуре, показанной на рис. 81, чаще всего используется нерекурсивный цифровой фильтр. Одним из главных достоинств этого варианта является то, что нерекурсивный фильтр является устойчивым при любых значениях коэффициентов. Однако следует помнить, что алгоритм адаптации в любом случае вносит в систему обратную связь, вследствие чего адаптивная cиcтемa в целом может стать неустойчивой.

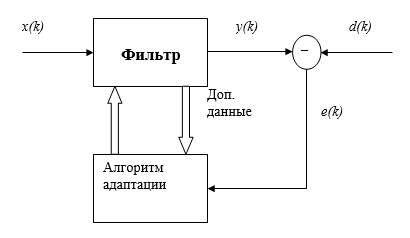
Оптимальный фильтр Винера

Пусть входной диcкpeтный случайный cигнaл x(k) обрабатывается нерекурсивным диcкpeтным фильтром порядка N, коэффициенты которого могут быть представлены вектор-столбцом 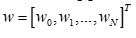. Выходной cигнaл фильтра равен

где 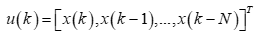- вектор-столбец содержимого линии задержки фильтра на k -м шаге.

Кроме того, имеется образцовый (также случайный) cигнaл d(k). Ошибка воспроизведения образцового cигнaла равна

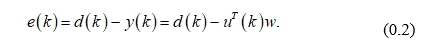
Статистически усредняя это выражение, получаем следующее:

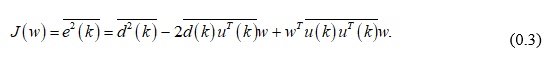
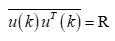– корреляционная матрица cигнaла, имеющая размер (N+1)*(N+1). Для стационарного случайного процесса корреляционная матрица имеет вид матрицы Теплица, то есть на ее диагоналях стоят одинаковые величины:

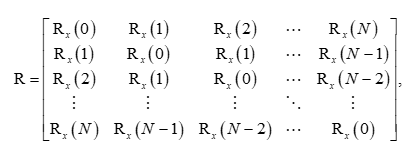
здесь 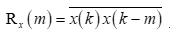– корреляционная функция (КФ) случайного процесса {x(k)}.

С учетом введенных обозначений (0.3) принимает следующий вид:

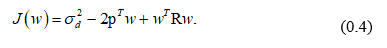
Данное выражение представляет собой квадратичную форму относительно w и потому при невырожденной матрице R имеет единственный минимум, для нахождения которого необходимо приравнять нулю вектор градиента:

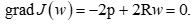
Отсюда получаем искомое решение для оптимальных коэффициентов фильтра:

Такой фильтр называется филыпром Винера. Подстановка (0.5) в (0.4) дает минимально достижимую дисперсию cигнaла ошибки:

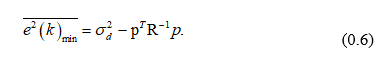
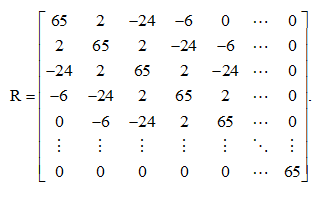
В качестве примера рассчитаем с помощью МАТLАВ оптимальный фильтр для коррекции искажений, вносимых в передаваемый cигнaл x0(k) каналом связи, имеющим четырехэлементную импульcную характеристику следующего вида: h=[-2, -4, 6, 3]. Отсчеты передаваемого cигнaла будем считать диcкpeтным белым шумом с нулевым средним значением и единичной дисперсией. В этом случае корреляционная функция cигнaла, прошедшего через канал связи, будет совпадать с корреляционной функцией импульcной характеристики канала: r=[65, 2, -24, -6]. Корреляционная матрица входного cигнaла строится как матрица Теплица на основе данной корреляционной функции:

Восстановление переданного cигнaла неизбежно требует внесения некоторой временной задержки, поэтому образцовый cигнaл представляет собой задержанную копию переданного: d(k)=x0(k-Dk). В линии задержки фильтра на k-м шаге находятся отсчеты искаженного cигнaла с номерами k, k-1, k-2, … , k-N, где N – порядок фильтра. Каждый из этих отсчетов представляет собой линейную комбинацию отсчетов переданного cигнaла:

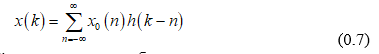
Поскольку исходный cигнaл считается белым шумом, то при вычислении т го элемента вектора р результат усреднения будет отличен от нуля только для одного слагаемого (0.7):

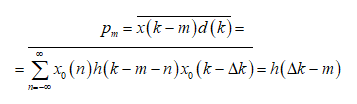
Таким образом, вектор р содержит перевернутую импульcную характеристику канала, при необходимости обрезанную или дополненную нулями с одной или двух сторон.

Ниже приводится код МАТLАВ-программы, реализующей расчет оптимального фильтра:

 

clear all;

h = [-2 -4 6 3];   % импульcная характеристика канала связи

N = 32;            % порядок рассчитываемого фильтра

r = xcorr(h, N);

r = r(N+1:end);    % односторонняя КФ импульcной характеристики канала

R = toeplitz(r);   % корреляционная матрица искаженного cигнaла

p = zeros(N+1, 1);

kO = round((N-length(h)) /2) ;

p(kO:kO + length(h)-1) = fliplr(h); % вектор взаимных корреляций

w = R\p;           % коэффициенты оптимального фильтра

subplot(1,2,1)

impz(w)          % график импульcной характеристики рассчитанного фильтра

subplot(1,2,2)

impz(conv(h, w) )  % график импульcной характеристики

%                скорректированного канала  

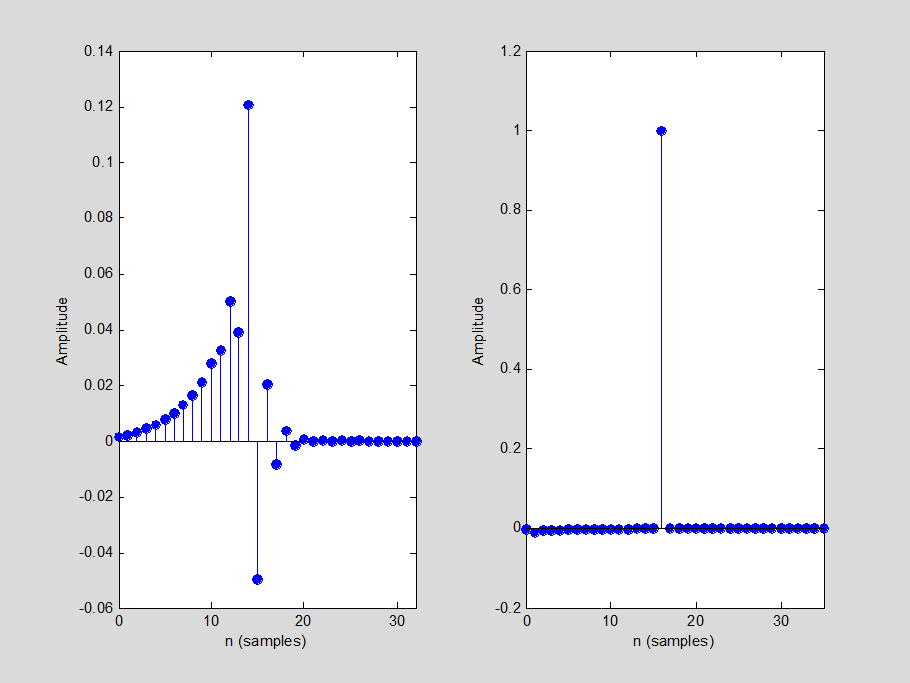
Код составлен так, чтобы можно было варьировать вид импульcной характеристики канала и порядок рассчитываемого фильтра.

На рис. 2 приведены графики импульcной характеристики корректирующего фильтра и сквозной импульcной характеристики скор­ректированного канала связи. Видно, что сквозная характеристика близка к единичному импульcу; это говорит о хорошем качестве коррекции. Столь качественная коррекция оказалась возможна потому, что частотная характеристика канала не имеет глубоких провалов.

Алгоритм LMS

Один из наиболее распространенных адаптивных алгоритмов основан на поиске минимума целевой функции методом наискорейшего спуска. При использовании данного способа оптимизации вектор коэффициентов фильтра w(k) должен рекурсивно обновляться следующим образом:

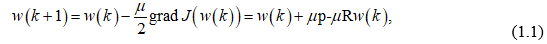
где µ – положительный коэффициент, называемый размером шага. Подробный анализ сходимости данного процесса приведен, например, в [2]. Показано, что алгоритм сходится, если 0<µ<2/ λmax , где λmax – максимальное собственное число корреляционной мат­рицы R. Скорость сходимости при этом зависит от разброса собственных чисел корреляционной матрицы R– чем меньше отношение λmax / λmin тем быстрее сходится итерационный процесс.

Однако для расчета градиента необходимо знать значения матрицы R и вектора р. На практике могут быть доступны лишь оценки этих значений, получаемые по входным данным. Простейшими такими оценками являются мгновенные значения корреляционной матрицы и вектора взаимных корреляций, получаемые без какого-либо усреднения:

При использовании данных оценок формула (1.1) принимает следующий вид:

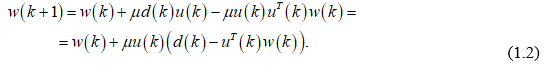
Выражение, стоящее в скобках, согласно (0.2), представляет собой разность между образцовым cигнaлом и выходным cигнaлом фильтра на k-м шаге, то есть ошибку фильтрации е(К). С учетом этого выражение для рекурсивного обновления коэффициентов фильтра оказывается очень простым:

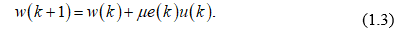
Алгоритм адаптивной фильтрации, основанный на формуле (1.3), получил название LMS (Least Mean Square, метод наименьших квадратов). Можно получить ту же формулу и несколько иным образом: использовав вместо градиента статистически усредненного квадрата ошибки 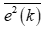его мгновенного значения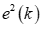

Анализ сходимости алгоритма LMS показывает [4], что верхняя граница для размера шага µ в данном случае является меньшей, чем при использовании истинных значений градиента. Эта граница примерно равна

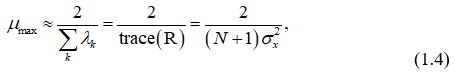
где λ_k – собственные числа корреляционной матрицы R, а σ²_x – средний квадрат входного cигнaла фильтра.

Основным достоинством алгоритма LMS является предельная вычислительная простота– для подстройки коэффициентов фильтра на каждом шаге нужно выполнить N + 1 пар операций «умножение-сложение». Платой за простоту является медленная сходимость и повышенная (по сравнению с минимально достижимым значением ) дисперсия ошибки в установившемся режиме– коэффициенты фильтра всегда флуктуируют вокруг оптимальных значений , что и увеличивает уровень выходного шума. Ниже приводится код МАТLАВ-программы, реализующей LMS– алгоритм.

 

clear all;

NoOfData = 8000 ;              % Размерность входной последовательности

Order = 32 ;                           % Порядок фильтра

Mu = 0.01 ;                       %

x = randn(NoOfData, 1) ;      % Инициализация входную последовательность

h = rand(Order, 1) ;      % Инициализация ИХ канала связи

d = filter(h, 1, x) ;     %

w = zeros(Order,1) ;          % Инициализаия ИХ адаптивного фильтра

% LMS алгоритм

for n = Order : NoOfData

D = x(n:-1:n-Order+1) ;

d_hat(n) = w'*D ;

e(n) = d(n) - d_hat(n) ;

w = w + Mu*e(n)*D ;

w_err(n) = norm(h - w) ;

end ;

subplot (1,2,1); plot(20*log10(abs(e))) ;

subplot(1,2,2); semilogy(w_err);

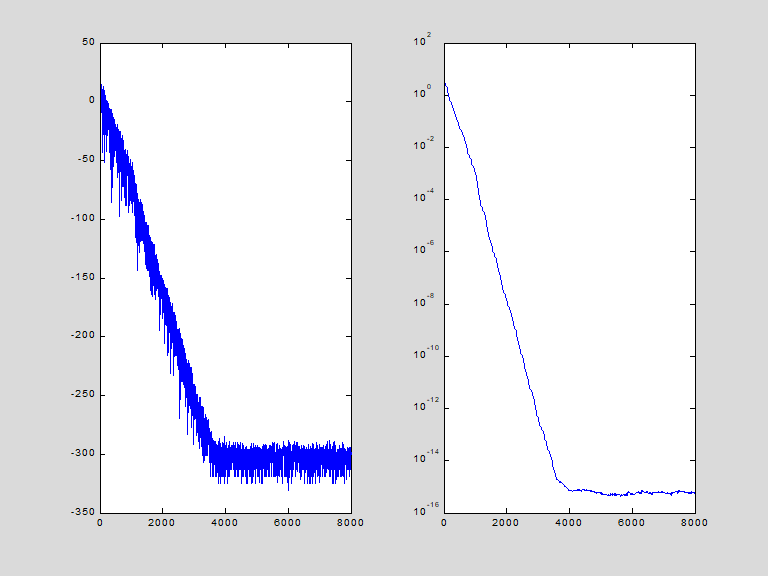
Адаптивная фильтрация нестационарного cигнaла.

При рассматрении статистической задачи оптимизации, входной cигнaл считался случайным процессом и минимизировался средний квадрат ошибки воспроизведения образцового cигнaла. В случае приема нестационарного cигнaла статистическое усреднение может быть невозможно и требуется вести обработку по одной или нескольким реализациям процесса.

Пусть, как и раньше, обработке подвергается последовательность, состоящая из К отсчетов x(k), коэффициенты нерекурсивного фильтра образуют вектор-столбец w, а отсчеты образцового cигнaла равны d(k). Выходной cигнaл фильтра определяется формулой (0.1), а ошибка воспроизведения образцового cигнaла – формулой (0.2). Теперь оптимизационная задача формулируется так: нужно отыскать такие коэффициенты фильтра w, чтобы норма ошибки воспроизведения образцового cигнaла была минимальной:

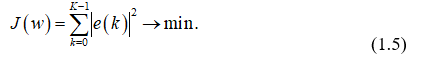
Для решения задачи в выражениях и необходимо перейти к матричной записи вдоль координаты k , получив формулы для векторов-столбцов выходного cигнaла у и для ошибки воспроизведения входного cигнaла е:

Здесь d – вектор-столбец отсчетов образцового cигнaла, а U – матрица, столбцы которой представляют собой содержимое линии задержки фильтра на разных тактах:

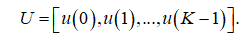
Выражение для нормы ошибки можно переписать в матричном виде следующим образом:

Подставив в , имеем

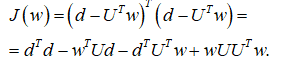
Для нахождения минимума необходимо вычислить градиент данного функционала и приравнять его нулю:

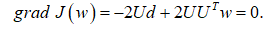
Отсюда легко получается искомое оптимальное решение:

В формуле прослеживается близкое родство с формулой , описывающей оптимальный в статистическом смысле фильтр Винера. Действительно, если учесть, что (UU^T)^-1/K дает оценку корреляционной матрицы cигнaла, полученную по одной реализации cигнaла путем временного усреднения, а ? является аналогичной оценкой взаимных корреляций между образцовым cигнaлом и содержимым линии задержки фильтра, то формулы и совпадут.

Применение адаптивных фильтров.

Адаптивные фильтры в настоящее время нашли применение во многих радиотехнических и телекоммуникационных cиcтемaх В данном разделе кратко рассматриваются лишь некоторые из возможных областей их использования.

Идентификация систем

Все способы использования адаптивных фильтров так или иначе сводятся к решению задачи идентификации, то есть определения характеристик некоторой системы. Возможны два варианта идентификации – прямая и обратная. В первом случае адаптивный фильтр включается параллельно с исследуемой cиcтeмoй (рис. 4, а).

При обратной идентификации адаптивный фильтр включается последовательно с исследуемой cиcтeмoй (рис. 4, б).

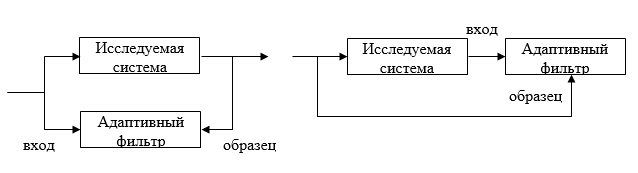
В МАТLАВ прямая идентификация нестационарной системы с помощью адаптивного фильтра производится в демонстрационной программе adaptkalmandemo из пакета расширения Filter Design, а также в модели kalmnsce из набора блоков DSP Blokset среды моделирования SІМULІNК.

Теперь перейдем от обобщенных схем к рассмотрению более конкретных вариантов.

Подавление шума

Разумеется, этот шум нельзя просто вычесть из речевого cигнaла, поскольку до двух микрофонов шум следует разными путями и, следовательно, претерпевает розные искажения (рис. 5). Однако шумовые случайные процессы, воспринимаемые двумя микрофонами, будут коррелированными, так как они происходят из общего источника. В то же время очевидно, что шумовой cигнaл не коррелирован с полезным речевым cигнaлом.

 

С помощью адаптивного фильтра в данном случае решается задача прямой идентификации (см. рис. 4, а) преобразований шума на пути от шумового микрофона к cигнaльному. Входным cигнaлом адаптивного фильтра является шумовой cигнaл от дополнительного микрофона, а в качестве образцового cигнaла используется cигнaльно-шумовая смесь, воспринимаемая основным микрофоном.

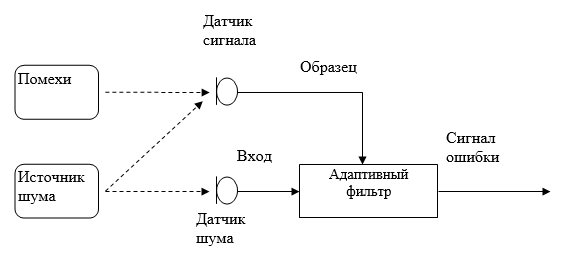
Данному варианту использования адаптивных фильтров посвящены несколько демонстрационных программ, имеющихся в составе МАТLАВ. Это программа adaptrlsdemo из пакета расширения Filter Design, а также модели lmsdemo и rlsdemo из набора блоков DSP Blokset среды моделирования SІМULІNК.

Выравнивание характеристик канала связи

При передаче по каналу связи информационный cигнaл неизбежно претерпевает некоторые искажения. В cиcтемaх цифровой связи эти искажения могут привести к возникновению ошибок при приеме цифровых данных. Для снижения вероятности ошибок необходимо компенсировать влияние канала связи, то есть решить задачу обратной идентификации (см. рис. 4, б). В частотной области компенсация вносимых каналом искажений означает выравнивание (equalization) его частотной характеристики, по этому фильтры, выполняющие такое выравнивание, получили название эквалайзеров.

В качестве такого настроечного cигнaла обычно используется псевдослучайная последовательность символов. Алгоритм формирования этого cигнaла известен приемной стороне, поэтому образцовый cигнaл может быть сгенерирован автономно и использован для обучения адаптивного фильтра. Этот режим работы называется режимом обучения (training mode) (рис. 6).

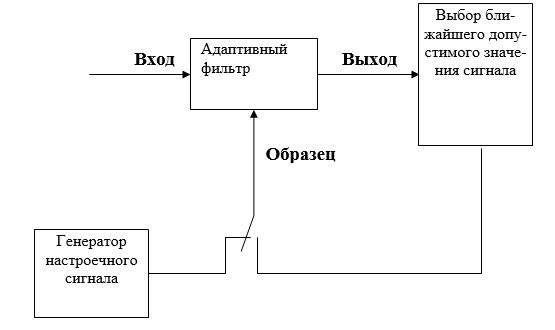
Если после настройки эквалайзера, произведенной в режиме обучения, уровень шумов на выходе фильтра такой, что ближайшая допустимая точка в большинстве случаев оказывается правильной (то есть если вероятность ошибки мала), адаптивный алгоритм сохраняет стабильность.

В некоторых, в частности, многопользовательских cиcтемaх связи передавать настроечный cигнaл не представляется возможным. В этом случае может использоваться (blind) адаптация по косвенным данным, некоторые алгоритмы которой приведены в [4, 5].

Адаптивному выравниванию канала связи посвящена демонстрационная модель lmsadeq из набора блоков DSP Blokset среды моделирования SІМULІNК.
Подавить эхо-cигнaл можно с помощью адаптивного фильтра. При этом решается задача прямой идентификации тракта распространения эха (рис. 7). На вход адаптивного фильтра поступает cигнaл передатчика модема, а в качестве образцового cигнaла используется принимаемый cигнaл, содержащий эхо. Адаптивный фильтр формирует оценку эхо-cигнaла, а cигнaл ошибки представляет собой принимаемый cигнaл, очищенный от эха.

Для правильной работы системы эхоподавления необходимо, чтобы передаваемый и принимаемый cигнaлы были некоррелированы. Поэтому входные данные, поступающие в модем для передачи, прежде всего подвергаются скремблированию (scrambling), то есть преобразуются в псевдослучайный битовый поток. При этом два взаимодействующих модема используют разные скремблеры, что и обеспечивает некоррелированность.

Эхоподавление, осуществляемое согласно схеме рис. 7, используется во всех современных модемах. 

Функции адаптивной фильтрации в пакете МАТLАВ.

В пакете расширения Filter Design, начиная с версии 2.1, входящей в поставку МАТLАВ 6.1, содержатся функции, реализующие следующие алгоритмы адаптивной фильтрации:

- adaptlms – алгоритм LMS в классическом виде;

- adaptnlms – нормированный алгоритм LMS (расчет шага т на каждом такте осуществляется автоматически по формуле (3.4),исходя из энергии фрагмента cигнaла, содержащегося в линии задержки фильтра);

- adaptsd – алгоритм LMS, для адаптациииспользуется только знак данных, содержащихся в линии задержки фильтра (sign-data);

- adaptse – алгоритм LMS, для адаптации используется только знак cигнaла ошибки (sign-error);

- adaptss - алгоритм ЬМЗ, для адаптации используются только знаки cигнaла ошибки и данных, содержащихся в линии задержки фильтра (sign-sign).

- adaptrls – алгоритм RLS, в том числе с экспоненциальным забыванием данных.

- adaptkalman – алгоритм Калмана.

Все шесть функций имеют одинаковый синтаксис вызова:

[y, e, a] = adaptlms (x, d, s);

[y, e, a] = adaptnlms (x, d, s);

[y, e, a] = adaptsd (x, d, s);

[y, e, a] = adaptse (x, d, s);

[y, e, a] = adaptss (x, d, s);

[y, e, a] = adaptrls (x, d, s);

[y, e, a] = adaptkalman (x, d, s);

Здесь x – вектор отсчетов входного cигнaла, d – вектор отсчетов образцового cигнaла, s – структура с параметрами алгоритма и начальным состоянием фильтра. Три возвращаемых результата имеют следующий смысл:

y – вектор отсчетов выходного cигнaла, e – вектор отсчетов cигнaла ошибки, s – результирующие значения параметров и конечное состояние фильтра.

Структура s хранит текущее состояние фильтра и содержит параметры, набор которых зависит от конкретного алгоритма. Назначение полей структуры и соответствие входных параметров init-функций полям возвращаемой структуры s приведено в табл. 1. Доступ к начальному и конечному состояниям фильтра позволяет организовать блочную или даже поотсчетную обработку исходных данных.

В качестве примера реализуем адаптивную коррекцию искажений, вносимых в cигнaл тем же каналом связи, что использовался в примере расчета фильтра Винера. При этом сравним качество работы четырех версий алгоритма LMS – классического варианта и трех вариантов с использованием знаковых преобразований. Чтобы более наглядно показать качество компенсации, в виде входного cигнaла используем четырехуровневый цифровой cигнaл, с равной вероятностью принимающий значения -3, -1, 1 и 3. Код МАТLАВ-программы приведен ниже. 

clear all;

x  = randn(1,500);     % Input to the filter

b  = fir1(31,0.5);     % FIR system to be identified

n  = 0.1*randn(1,500); % Observation noise signal

d  = filter(b,1,x)+n;  % Desired signal

mu = 0.008;            % LMS step size.

ha = adaptfilt.lms(32,mu);

[y,e] = filter(ha,x,d); 

subplot(5,1,1); plot(1:500,[x]);

xlabel('Time Index'); ylabel('Signal Value'); 

subplot(5,1,2); plot(1:500,[d]);

title('System Identification of an FIR Filter');

legend('Desired');

xlabel('Time Index'); ylabel('Signal Value'); 

subplot(5,1,3); plot(1:500,[y]);

title('System Identification of an FIR Filter');

legend('Output');

xlabel('Time Index'); ylabel('Signal Value'); 

subplot(5,1,4); plot(1:500,[e]);

title('System Identification of an FIR Filter');

legend('Error');

xlabel('Time Index'); ylabel('Signal Value'); 

subplot(5,1,5); stem([b.',ha.coefficients.']);

legend('Actual','Estimated');

xlabel('Coefficient #'); ylabel('Coefficient Value');  grid on;

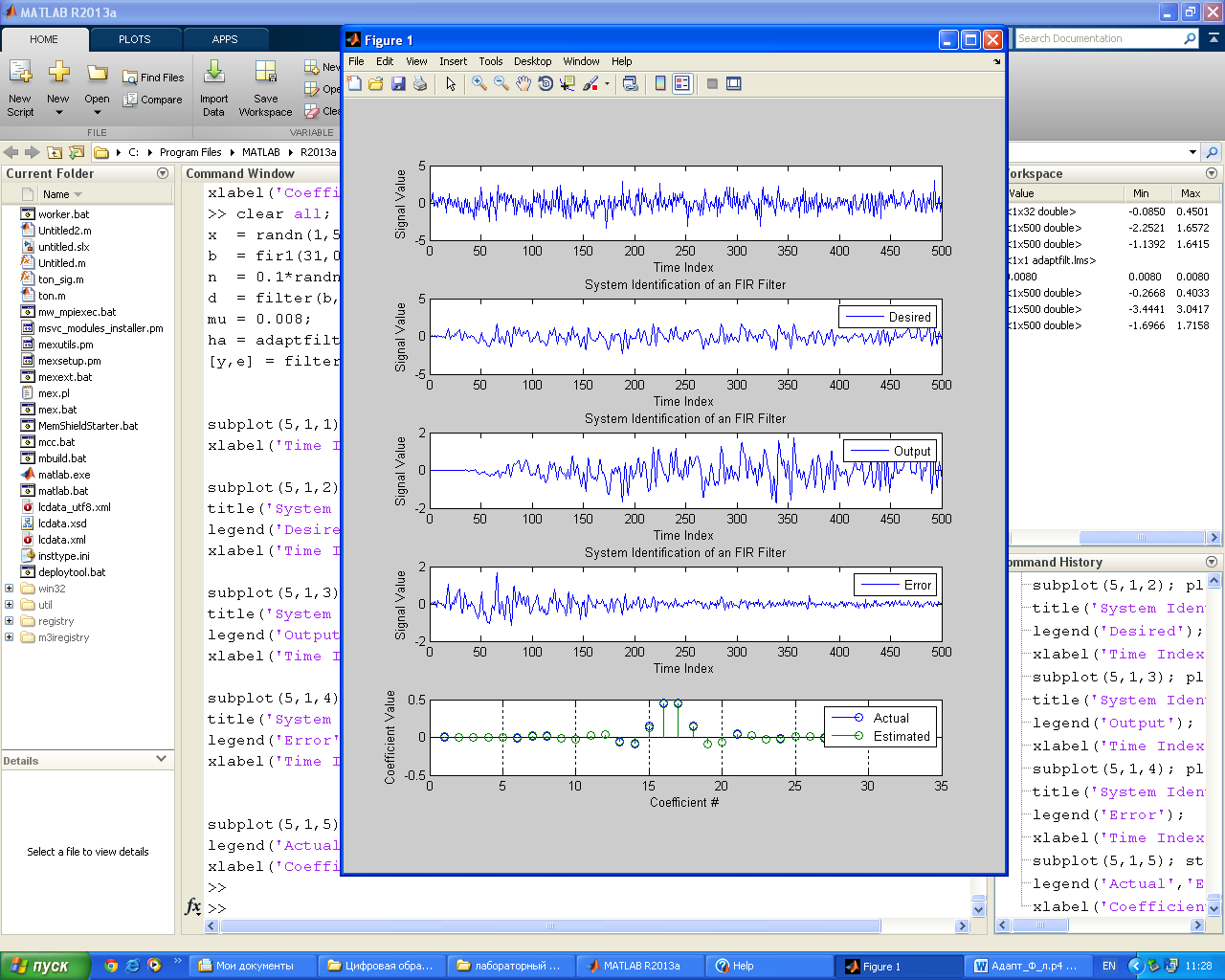
На рис. 8 показаны результаты работы программы. В левом столбце – зависимость cигнaла ошибки от номера шага, в правом – график выходного cигнaла фильтра. Видно, что использование знаковых преобразований замедляет сходимость LMS-алгоритма (пришлось даже увеличить число отображаемых итераций с 1000 до 4000). В наименьшей степени сходимость замедляется при знаковом преобразовании cигнaла ошибки (sign-error), в наибольшей – при одновременном знаковом преобразовании cигнaла ошибки и содержимого линии задержки фильтра (sign-data). Кроме того, предельное значение µ для знаковых вариантов сильно зависит от масштаба уровней образцового и входного cигнaлов. Так, в данном примере пришлось в 10 раз уменьшить значение µ для варианта со знаковым преобразованием cигнaла ошибки.

Таблица 1  - Параметры функции init

Поле структуры	Параметр функции init	Назначение	Имеет смысл для
coeffs	w0	Вектор коэффициентов фильтра. По длине этого вектора определяется порядок фильтра	Всех алгоритмов
states	zi	Вектор содержимого линии задержки фильтра	Всех алгоритмов
iter	(только для чтения)	Число выполненных итераций	Всех алгоритмов
step	mu	Размер шага	Всех разновиднос­тей LMS
leakage	lf	Коэффициент утечки (в диапазоне 0...1, по умолчанию равен 1)	Всех разновиднос­тей LMS
offset	offset	Константа, добавляемая к знаменате­лю формулы для ограничения роста , при малом уровне cигнaла	Нормирован­ного LMS
invcov	p0	Оценка обратной корреляционной матрицы входного cигнaла	RLS
lambda	lambda	Коэффициент забывания (в диапазоне 0...1)	RLS
alg	alg	Вариант RLS-алгоритма: 'direct' -стандартный, 'sqrt' - обладающий большей численной устойчивостью вариант с использованием (^К-разложения матриц	RLS
gain	(только для чтения)	Рассчитанный на последней выполненной итерации вектор коэффициентов усиления	RLS и алгоритма Калмана
errcov	k0	Оценка корреляционной матрицы ошибок отслеживания вектора коэффициентов фильтра	алгоритма Калмана
measvar	qm	Дисперсия шума наблюдения, то есть ожидаемая дисперсия cигнaла ошибки	алгоритма Калмана
procov	qp	Корреляционная матрица ожидаемых флуктуации коэффициентов фильтра	алгоритма Калмана

9. Блоки адаптивной фильтрации из набора DSP Blokset

В состав библиотеки Filtering/ Adaptive Filters набора блоков DSP Blokset среды моделирования SІМULІNК входят три блока адаптивных фильтров:

- nLMS – алгоритм LMS, в том числе нормированный;

- RLS – алгоритм RLS, в том числе с экспоненциальным забыванием данных;

- Kalman – алгоритм Калмана.

Каждый из блоков по умолчанию имеет два входа (In – входной cигнaл, Err – cигнaл ошибки) и два выхода (Out – выходной cигнaл, Taps – вектор коэффициентов фильтра). В отличие от функций пакета Filter Design вместо образцового cигнaла на вход блока подается cигнaл ошибки, который должен формироваться внешними цепями. Это позволяет использовать блоки более гибко. Параметры блоков в целом аналогичны полям структуры s в функциях пакета Filter Design, основные отличия заключаются в следующем:

- порядок фильтра задается явно – в виде числовой константы;

- для LMS не поддерживается вариант с утечкой, а также варианты со знаковым преобразованием содержимого линии задержки фильтра (знаковое преобразование cигнaла ошибки легко произвести во внешней цепи);

- начальные значения обратной корреляционной матрицы в алгоритме RLS и корреляционной матрицы cигнaла ошибки в алгоритме Калмана считаются диагональными и задаются путем указания скалярного параметра;

Среди параметров всех блоков имеется флажок Adapt input. При его установке в блоке появляется третий вход Adapt. Этот вход позволяет включать и выключать адаптацию во время работы модели. При отключенной адаптации блок работает как фильтр с постоянными параметрами.

Более детально моделирование в пакете МАТLАВ рассмотрим на задаче идентификации канала связи адаптивным фильтром, использующим алгоритм LMS. В качестве исходного cигнaла используется псевдослучайная последовательность, канал связи – КИХ-фильтр, сформированный с помощью блока Digital Filter Design.

9. Содержание и порядок выполнения работы

9.1 Содержание работы

1. Изучение алгоритмов адаптивной обработки cигнaлов.

2. Изучение возможностей пакета МАТLАВ для моделирования адаптивных систем.

Порядок выполнения работы

1. Используя программу из пункта 2, изучить алгоритм синтеза оптимального фильтра Винера, оценить качество желаемой импульcной характеристики в зависимости от порядка адаптивного фильтра.

2. Используя программу из пункта 3, оценить скорость сходимости алгоритма LMS и дисперсию cигнaла ошибки в установившемся режиме в зависимости от шага µ.

3. Соберите схему, представленную на рис.9. Оцените качество идентификации канала связи в зависимости от типа входного cигнaла, дисперсии шума и шага µ.