1 Обзор литературы. Научная новизна, цель, метод, объект и практическая значимость исследования

Магнитоэлектрический эффект относится к перекрестным эффектам и сам по себе уже представляет интерес для исследований, поскольку в магнитоэлектрических материалах наблюдается взаимосвязь процессов намагничивания и поляризации. В области магнитного резонанса магнитоэлектрический эффект проявляется в сдвиге резонансной линии под действием электрического поля. Это позволяет на основе магнитоэлектрического эффекта создать приборы функциональной электроники, в которых управление осуществляется не только магнитным, но и электрическим полями. К настоящему времени проведен большой объем исследований магнитоэлектрического эффекта на низких частотах, однако в области магнитного резонанса этот эффект изучен недостаточно. Практическому использованию магнитоэлектрического эффекта монокристаллов в твердотельной электронике препятствует малая величина эффекта. Развитие технологии изготовления композиционных материалов позволило создать магнитоэлектрические феррит-пьезоэлектрические структуры. Величина магнитоэлектрического эффекта в композитах значительно больше, чем в монокристаллах. В композиционных материалах магнитоэлектрический эффект возникает вследствие механического взаимодействия магнитной и пьезоэлектрической подсистем, поэтому следует ожидать, что на частоте электромеханического резонанса будет наблюдаться увеличение магнитоэлектрического эффекта. Между тем, ни теоретического, ни экспериментального исследования частотной зависимости магнитоэлектрических коэффициентов в области акустических частот проведено не было. Магнитоэлектрический эффект заключается в индуцировании электрической поляризации в материале во внешнем магнитном поле или в появлении намагниченности во внешнем электрическом поле. Общим для монокристаллических материалов является то, что магнитоэлектрический эффект наблюдается в большинстве из них при температурах, значительно ниже комнатной. Это связано с низкими температурами Нееля или Кюри для этих материалов. Магнитоэлектрические коэффициенты обращаются в нуль, как только температура приближается к точке перехода в неупорядоченное состояние. Кроме того, монокристаллические материалы характеризуются малыми значениями магнитоэлектрических коэффициентов, величина которых недостаточна для практического использования этих материалов. В значительной степени от указанных недостатков свободны композиционные материалы на основе ферритов и пьезоэлектриков. Для композиционных материалов открываются широкие возможности варьирования их физических свойств, а значит и оптимизации характеристик устройств на их основе. Температурная зависимость магнитоэлектрического эффекта в антиферромагнетиках может быть использована для определения температуры Нееля. Такая возможность обусловлена тем, что магнитоэлектрическая восприимчивость обращается в нуль при температурах выше температуры Нееля. Достоинством композиционных материалов является то, что магнитоэлектрический эффект в них может быть использован для определения температуры Кюри для сегнетоэлектрической фазы. Кроме того, структура тензора магнитоэлектрической восприимчивости может быть использована при уточнении симметрии кристаллических структур фаз слоистого композита. Магнитоэлектрическая восприимчивость и магнитоэлектрический коэффициент по напряжению определяются параметрами фаз композита и их объемными долями. Поэтому измеренные значения магнитоэлектрических параметров могут быть использованы при определении таких параметров исходных компонент композита, как коэффициенты жесткости, податливости, пьезоэлектрические коэффициенты, диэлектрическая и магнитная проницаемости, пьезомагнитные модули. Параметры максвелл-вагнеровской релаксации и резонансной дисперсии магнитоэлектрических параметров также могут быть использованы для уточнения таких параметров фаз, как электрическая проводимость, диэлектрическая проницаемость и т.п. Известно, что магнитная восприимчивость феррита имеет резонансную зависимость от внешнего постоянного электрического поля. Наблюдение магнитного резонанса в феррите становится возможным в электрическом поле при использовании слоистого композиционного материала, в котором одной из компонент является исследуемый феррит. Указанный метод наблюдения ферромагнитного резонанса во внешнем постоянном электрическом поле основан на эффекте изменения частоты магнитного резонанса при воздействии на образец внешнего постоянного электрического поля. При этом система магнитной развертки может быть упрощена или исключена, а для перестройки частоты магнитного резонанса используется источник напряжения. Одним из перспективных направлений использования композиционных феррит-пьезоэлектрических материалов является создание датчиков физических величин с широким частотным диапазоном. Керамическая технология изготовления композиционных материалов обуславливает их низкую стоимость по сравнению с монокристаллическими и поликристаллическими материалами и позволяет изготавливать датчики в микроэлектронном исполнении. В качестве примеров таких устройств можно указать датчики постоянного и переменного магнитного поля на основе многослойных и объемных композиционных магнитоэлектрических материалов, пригодные для промышленного изготовления с применением микроэлектронной технологии. Магнитоэлектрический эффект в твёрдом теле был предсказан Л.Д.Ландау и Е.М.Лифшицем в 1957 г. [1]. Для феноменологического материала, помещенного в однородные магнитное и электрическое поля, изменение объемной плотности свободной энергии может быть выражено следующим образом:

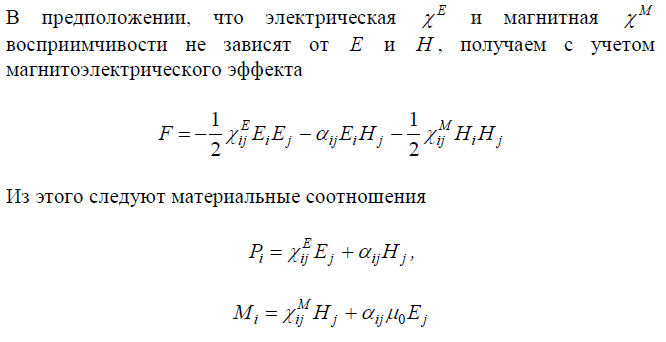
Тензор магнитоэлектрической восприимчивости в общем случае является тензором второго ранга. И.Е. Дзялошинский теоретически показал, что среди веществ с известной магнитной структурой имеется, по крайней мере, один кристалл, а именно оксид хрома, в котором должен иметь место магнитоэлектрический эффект [2]. В 1960г. Д. Н. Астров экспериментально обнаружил магнитоэлектрический эффект в оксиде хрома [3] и измерил продольную и поперечную магнитоэлектрический восприимчивости. В измерительной установке Астрова регистрировался переменный магнитный момент, возникающий в образце под действием приложенного электрического поля. Измерения проводились на частоте 10 кГц. Затем Folen et al. [4] измерили магнитоэлектрический эффект, индуцированный магнитным полем. Эти измерения были проведены также на оксиде хрома довольно простым способом: монокристаллический образец помещался между полюсами электромагнита, а электроды, нанесённые методом осаждения на обе стороны образца, подсоединялись к вакуумному электрометру. При включении электромагнита электрометром измеряли напряжение, возникающее в образце. Этот же статический метод применял Ascher E. [5] при исследовании Ni₃B₇O₁₃I. Была рассмотрена связь магнитоэлектрического эффекта с симметрией кристаллической структуры [4], в частности, установлено, что произведение a_ijE_iH_j отлично от нуля только в магнитоупорядоченных материалах. Предложены теоретические модели наблюдаемого магнитоэлектрического эффекта в некоторых материалах [5-7]. Проведена классификация магнитоэлектрических материалов по магнитным точечным группам [8] и рассмотрена магнитоэлектрическая симметрия материалов [9]. Было проведено объяснение магнитоэлектрического эффекта на основе статистической теории [10, 11]. Изучалось распространение волн в магнитоэлектрических средах [12, 13]. В 1982 г. был предложен новый подход к изучению магнитоэлектрического эффекта в ферримагнетиках [14], согласно которому плотность магнитной энергии может быть разложена в ряд по степеням намагниченности, а симметрия тензорных коэффициентов этого ряда определятся, главным образом, симметрией парафазы кристалла. Вклад в развитие теории магнитоэлектрического эффекта внесли также Шавров В.Г. [15], Alexander S., Shtrikman S. [16], Asher E. [17]. Rado [18-19] обнаружил линейный магнитоэлектрический эффект в ферримагнитном материале. Ga_2-xFe_xO₃ . Этот эффект был объяснен наличием пьезоэлектрических и пьезомагнитных свойств материала. Примером материала, обладающего квадратичным магнитоэлектрическим эффектом, является борат железа 3 FeBO₃ [20]. К настоящему времени изучено большое количество монокристаллических магнитоэлектрических материалов. Наиболее подробно свойства магнитоэлектрических материалов рассмотрены в [21-26].Общим для этих материалов является то, что магнитоэлектрический эффект наблюдается в большинстве из них при температурах, значительно ниже комнатной. Это связано с низкими температурами Нееля или Кюри для этих материалов. магнитоэлектрические коэффициенты обращаются в нуль, как только температура приближается к точке перехода в неупорядоченное состояние. Кроме того, монокристаллические материалы характеризуются малыми значениями магнитоэлектрических коэффициентов, величина которых недостаточна для практического использования этих материалов. В значительной степени от указанных недостатков свободны композиционные материалы на основе ферритов и пьезоэлектриков [27]. Современный прогресс в науке и технике неразрывно связан с развитием наших знаний в области композиционных материалов. Спектр применений композиционных материалов чрезвычайно широк - от космических аппаратов до бытовых приборов. Важное место среди известных композиционных материалов занимают материалы, уникальные свойства которых обусловлены существованием магнитоэлектрического эффекта. В отличие от монокристаллов магнитоэлектрический эффект в композиционных материалах представляет собой так называемый «вторичный» эффект в цепочке «магнитострикция – упругая деформация – пьезоэлектрический эффект» и благодаря подбору компонентов с высокими магнитострикционными и пьезоэлектрическими константами удается получить величину магнитоэлектрического эффекта, необходимую для практического использования. Магнитоэлектрический эффект относится к перекрестным эффектам и сам по себе уже представляет интерес для исследований, поскольку наблюдается только в определенных материалах. Магнитоэлектрический эффект заключается в индуцировании электрической поляризации в материале во внешнем магнитном поле или в появлении намагниченности во внешнем электрическом поле:

Для композиционных материалов открываются широкие возможности варьирования их физических свойств, а значит и оптимизации характеристик устройств на их основе. Магнитоэлектрический эффект в композиционных материалах можно рассматривать как результат взаимодействия пьезоэлектрических и пьезомагнитных свойств. Механизм магнитоэлектрического эффекта состоит в следующем: пьезомагнитный материал деформируется при приложении внешнего магнитного поля. Эта деформация приводит к возникновению механических напряжений в пьезоэлектрической компоненте, а, следовательно, и к электрической поляризации, появляющейся вследствие пьезоэлектрического эффекта. Очевидно, возможен и обратный эффект. Внешнее электрическое поле вызывает деформацию пьезоэлектрической компоненты, приводящую к возникновению механических напряжений в пьезомагнитной компоненте. Пьезомагнитная компонента намагничивается благодаря пьезомагнитному эффекту. Таким образом, композиционный материал характеризуется новым свойством – магнитоэлектрическим эффектом, заключающимся в возникновении электрической поляризации во внешнем магнитном поле и в намагничивании во внешнем электрическом поле.Большинство известных магнитоупорядоченных материалов обладают магнитострикцией. Однако, пьезомагнитный эффект в этих материалах не наблюдается [28]. Это означает, что деформация материала, обусловленная внешним магнитным полем, зависит от величины поля не линейно, а квадратично. По этой причине магнитоэлектрический эффект в композиционных материалах является нелинейным эффектом, в то время как магнитоэлектрический эффект в монокристаллических материалах линеен в широком диапазоне значений электрического и магнитного полей. Это затрудняет использование композитов в линейных устройствах. Линеаризовать магнитоэлектрические свойства композиционных материалов можно приложением к материалу подмагничивающего поля. В этом случае в интервале магнитных полей, малых по сравнению с подмагничивающим полем, магнитоэлектрический эффект будет близок к линейному. В работе [29] приведены результаты измерений магнитоэлектрического эффекта в керамических композитах состава BaTiO₃ – NiFe₂O₄ легированных кобальтом и марганцем. Максимальная величина магнитоэлектрического коэффициента по напряжению составила . Авторы привели описание особого метода поляризации образцов, в котором изменялась полярность поля при температуре Кюри [30]. Использование поля, создаваемого пространственными зарядами в композите, позволило повысить степень поляризации образца. В работе [31] сообщено об исследовании керамических магнитоэлектрических композитов той же системы с избытком T_iO₂ влиянии размера частиц, скорости охлаждения и молярной концентрации обеих фаз композита. Для керамических композитов состава BaTiO₃ – Ni(Co,Mn)Fe₂O₄ удалось получить магнитоэлектрический коэффициент по напряжению . Bunget и Raetchi сообщили о наблюдении магнитоэлектрического эффекта в композитах состава Ni-Zn феррит-ЦТС и его зависимости от величины приложенного магнитного поля [32, 33]. Большое значение для решения прикладных задач имеет исследование магнитоэлектрического эффекта в слоистых композитах на основе магнитострикционных металлов , сплавов (пермендюр, терфенол) и пьезокерамики ЦТС [34-36]. В работах [37-39] получен максимальный магнитоэлектрический эффект величиной 5В/А в многослойных структурах на основе терфенола и ЦТС. Этот результат открывает реальную возможность их практического применения. Впервые исследование магнитоэлектрического эффекта в слоистых структурах феррит-пьезоэлектрик провели Бичурин М.И., Петров В.М [40]. Детальный анализ резонансных магнитоэлектрических эффектов в парамагнитных и магнитоупорядоченных средах проведен Бичуриным М.И. [41], микроскопическая теория магнитоэлектрического эффекта в области магнитного резонанса в магнитоупорядоченных кристаллах с - ионами представлена в [42, 43], низкочастотная теория магнитоэлектрического эффекта и дисперсионные свойства в [44], теория магнитоэлектрического эффекта в гомогенных композитах и гетерогенных структурах в [43], применение магнитоэлектрического эффекта и устройства на его основе в [45, 46]. В 2005 г. опубликован обзор Fiebig [47], в котором дан анализ основных работ по композиционным магнитоэлектрическим материалам. Оценка магнитоэлектрического коэффициента по напряжению в композитах, основанная на приближенной модели, приведена в [48]. Для наблюдения магнитоэлектрического эффекта в композитах, необходимо приложить к образцу постоянное подмагничивающее поле, совпадающее по направлению с переменным магнитным полем. Подмагничивающее поле может быть создано постоянным магнитом или электромагнитом. Bunget и Raetchi предложили другой метод измерений [32, 33]. Поскольку в магнитоэлектрических композитах электрическая поляризация есть функция электрического и магнитного полей, можно приложить их одновременно и измерять поляризацию. Авторы измерили поляризацию, поддерживая электрическое поле постоянным и изменяя магнитное поле. Таким образом, отношение изменения поляризации к приращению магнитного поля дает магнитоэлектрическая восприимчивость. Newnham et al. предложили классификацию композитов по типам связности [49]. Композит, одна фаза которого имеет связность во всех трех направлениях (обозначается индексом 3) и изолированной второй фазой, не имеющей связности ни в одном направлении (обозначается индексом 0), называется композитом со связностью типа 3-0. В магнитоэлектрических композитах магнитострикционная фаза, обычно феррит, имеет значительно меньшее сопротивление, чем пьезоэлектрическая фаза. Это ведет к сильной зависимости сопротивления композита от связности фаз, причем самое высокое сопротивление имеет место при последовательном включении компонент композита, самое низкое – при параллельном соединении. Некоторые из ферритов – полупроводники, в которых сопротивление сильно снижается при повышении температуры. Для наблюдения магнитоэлектрического эффекта в композите необходимо его поляризовать, чтобы пьезоэлектрический эффект в пьезоэлектрической компоненте был максимально возможным. Однако, электрическая поляризация этих материалов затруднена уже при комнатной температуре, тем более при более высокой температуре из-за высокой проводимости феррита. Использование композита с типом связности 3-0 позволяет повысить сопротивление и облегчает поляризацию. В композитах с типом связности 2-2 слои составляющих фаз чередуются, так что каждая фаза имеет связность в двух направлениях в плоскости слоев, но не связана с другим слоем той же самой фазы. В работах Harshe et al. [50, 51] приведены результаты расчета магнитоэлектрического коэффициента по напряжению для композитов с типом связности 2-2. При этом в [50] магнитоэлектрический коэффициент по напряжению вычислялся как отношение индуцированного электрического поля в пьезоэлектрической компоненте к магнитному полю, прикладываемому к магнитной компоненте aE=Pe/Mh Известны результаты измерений магнитоэлектрического эффекта в объемных композитах состава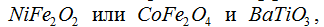

полученных спеканием порошка ферритов и титаната бария [52]. Образцы в форме тонких дисков поляризованы электрическим полем перпендикулярно их плоскости. магнитоэлектрический коэффициент измерен для двух случаев: ( ) поперечных полей, когда постоянное и переменное магнитные поля параллельны друг другу, а также плоскости диска (1,2) и перпендикулярны переменному электрическому полю (направление 3); ( ) продольных полей, когда все три поля параллельны друг другу и перпендикуляру к плоскости образца. Керамические объемные композиты, вообще говоря, обнаруживают магнитоэлектрическая связь более слабую, чем расчетные значения [53]. Одна из причин такого положения - низкое удельное сопротивление ферритов, что ( ) ограничивает электрическое поле при поляризации образцов, ведя к недостаточной степени поляризации и ( ) ведет к появлению тока утечки в образце, который приводит к уменьшению зарядов, индуцированных посредством пьезоэлектрического эффекта. Существенным достоинством объемных композиционных материалов является то, что они позволяют посредством выбора компонентов материала с необходимыми значениями электрической и магнитной проницаемостей и путем варьирования процентного содержания компонентов достичь требуемых значений заданного комплекса параметров. Кубические модели феррит-сегнетоэлектрического материала со связностью 3-0 и 0-3 рассмотрены в [53]. В указанной работе произведен численный расчет магнитоэлектрического коэффициента, равного отношению электрического поля, возникающего в композите, к магнитному полю. Однако, построить адекватную теоретическую модель не удалось: экспериментально наблюдаемое значение магнитоэлектрического коэффициента по напряжению (9,5*10^-3B/A) оказалось более чем на два порядка меньше теоретического ( ). В работах Nan et al. развит метод расчета магнитоэлектрического эффекта в объемных композитах на основе функций Грина и теории возмущений [34, 35]. Авторами предложен перспективный трехфазный композиционный материал, обладающий высокими механическими и магнитоэлектрическими свойствами. В работе [54] сообщается об экспериментально измеренном значении магнитоэлектрического коэффициента по напряжению 38 мВ/А для композита состава 0.8 ЦТС - /0.2 феррит кобальта. Команда китайских ученых с помощью ab initio расчетов предсказала магнитоэлектрический эффект в двойном слое графена [55]. Авторами рассмотрены свойства ленты графена зигзагообразной формы, для которой ранее предсказывали наличие двух магнитных подрешеток [56], что дает магнитные моменты противоположного знака на краях ленты. Также появлялись сообщения о скрытых сегнетоэлектрических свойствах такой ленты [57]. Так что вполне логично было задаться вопросом, а не возникает ли в ней под действием электрического поля пропорциональный ему магнитный момент, т.е. имеет ли место линейный магнитоэлектрический эффект? Оказывается, такой эффект можно смоделировать в системе из двухслойной ленты графена на подложке из кремния. В этом случае нижний слой ленты образует sp³ связи с подложкой и не проявляет магнитных свойств, а верхний слой графена, в силу слабости связи с нижележащим слоем, сохраняет свойства свободной ленты и, соответственно, на краях ленты образуются магнитные моменты противоположного знака. Возникает ситуация, при которой, вследствие обменного расщепления, на левом краю электроны со спином вверх формируют валентную зону, а электроны со спином вниз – зону проводимости (у правого края, соответственно, наоборот). Приложение напряжения смещения между подложкой и верхним слоем приводит к тому, что электроны, поступающие из подложки, заполняют преимущественно уровни энергии электронов валентной зоны, тем самым, приводя к изменениям магнитных моментов обоих краев, пропорциональным приложенному полю В отличие от классического линейного магнитоэлектрического эффекта, обусловленного смещением атомов под действием электрического поля (которое, в свою очередь, изменяет зоны перекрытия электронных облаков и обменное взаимодействие магнитных ионов), в данной разновидности магнитоэлектрического эффекта электрическое поле изменяет обменное расщепление электронных состояний на краю ленты. Отметим здесь, что для обычного линейного магнитоэлектрического эффекта характерна обратимость – электрическая поляризация также может быть порождена магнитным полем, но вопрос об обратимости эффекта в графене остался за пределами рассмотрения работы. Магнитоэлектрический эффект в материалах может найти широкое применение. Однако, этому препятствует плохая воспроизводимость магнитоэлектрических параметров композитов. Кроме того, фазы композита не должны вступать в химическую реакцию, а для достижения максимального магнитоэлектрического эффекта необходимо хорошее механическое сцепление. Для получения композитов на основе пьезоэлектрической керамики и ферритов путем спекания или методом направленной кристаллизации используется очень высокая температура обработки, при этом сложно избежать химической реакции фаз. Вид связности компонент имеет большое значение для физических параметров, таких как диэлектрическая проницаемость, пьезомодули и, следовательно, магнитоэлектрические коэффициенты. Возможные применения магнитоэлектрических материалов были рассмотрены ранее [22, 23, 27, 58, 59]. Фазовращатели СВЧ диапазона, построенные на основе магнитоэлектрического материала, рассмотрены в [45]. Разработке магнитоэлектрических датчиков магнитного поля и СВЧ мощности посвящена работа [46]. Для таких применений магнитоэлектрические композиционные материалы являются наиболее подходящими благодаря широкому рабочему температурному диапазону, а также благодаря более высоким значениям магнитоэлектрических коэффициентов по сравнению с монокристаллическими магнитоэлектрическими материалами. Разнообразные по физической природе волновые процессы в неоднородных средах, при математическом рассмотрении приводят к уравнениям, имеющим общие свойства. Первые работы по теории волновых процессов были посвящены распространению сигнала по цепочке точечных частиц, и лишь позднее началось изучение распространения волн в сплошных средах. Ньютон в 1686г. при вычислениях скорости звука рассмотрел одномерную решетку [60]. В 1753 году Д. Бернулли установил принцип суперпозиции для колебательных систем, обобщения которого привели к теореме Фурье в 1807 г., однако еще в 1754 г. Клеро в одной из своих работ по небесной механике, оставшейся незамеченной, дал необходимое доказательство указанной теоремы. Эйлер впервые решил задачу о колебаниях струны, а переход от непрерывного к дискретному установил Лагранж, связав результаты работ Бернулли и Эйлера. В 1831 г. Кельвин ввел понятие предельной частоты дискретных структур и объяснил дисперсию света [61]. Эти исследования позволили ему создать современные представления о структуре оптических сред. В 1912 г. М. Борн изучал распространение упругих волн в кристаллах. Дискретные структуры исследовал также Резерфорд [62], где он применял полиномы Чебышева – Гегенбауэра [63]. Подробные исследования волновых явлений акустики, механики, электромагнетизма и квантовой механики в дискретных периодических структурах провели Бриллюэн Л. и Пароди М. [64]. В своих исследованиях они широко использовали полиномы Гегенбауэра-Чебышева. В этой же работе подробно исследуются двух – и трехмерные решетки - однородные кристаллы, уравнения Хилла и Матье [65]. Невозможность точного решения уравнений динамики для неоднородных сред вынуждает прибегать к различным упрощениям и построению приближенных решений. При построении решений волновых уравнений в слоисто-неоднородных средах, когда параметры среды зависят лишь от одной пространственной координаты, широко используется модель кусочно-постоянной или слоисто-однородной среды. В этой модели среда задается пачками однородных слоев, разделенных плоскими границами разрыва параметров среды. Точное решение волновых уравнений в известных функциях допускает лишь узкий класс неоднородных сред, который практически весь приведен в монографии Бреховских Л.М. [66]. Отдельные случаи, допускающие построения точных решений для упругих сред при учете взаимной трансформации волн, рассмотрены в работе Завадского В.Ю. [67], в случае нормального падения электромагнитной волны на неоднородный диэлектрик в работе Козлова И.П. [68]. Среди методов исследования слоисто-неоднородных изотропных и анизотропных сред, не связанных с матричными методами, отметим применение группы вращения к решению задач отражения света стратифицированной анизотропной средой [69], применение метода возмущения [70], координатного метода [71]. Практически во всех работах рассматриваются частные случаи анизотропии (кубическая, гексагональная) или отсутствуют алгоритмы решения. В работе Петрашеня [72] сделана попытка численной реализации и построения алгоритмов численных расчетов с применением лучевых разложений. В виду громоздкости и малоэффективности эта работа не получила дальнейшего развития. Одним из наиболее известных специалистов в области изучения волновых процессов в анизотропных средах является академик Федоров Ф. И. Исследования по распространению упругих волн в анизотропных средах изложена в его классической монографии «Теория упругих волн в кристаллах» [73]. Однако даже в этой работе основное внимание уделено закономерностям распространения волн вдоль особых направлений и построению методов определения указанных направлений, что отражает еще раз сложность и разнообразие волновых процессов в упругих анизотропных средах. Следующая монография Федорова Ф.И. «Теория гиротропии» была посвящена изучению электромагнитных волн [74]. В этой работе изложен алгоритм построения точного решения уравнений Максвелла для анизотропных сред. Построенный им алгоритм, в принципе, позволяет получить решения. Однако сам этот алгоритм включает последовательное решение достаточно сложных задач и состоит, по существу, из нескольких самостоятельных проблем. В случае упругих анизотропных сред описание волновых процессов сводится к исследованию существенно более сложных громоздких уравнений движения среда, чем в случаях изотропии. Если же учесть известный факт, что изучение волновых полей даже в изотропных неоднородных средах – дело далеко не простое, то можно получить некоторое представление о тех затруднениях, с которыми нам предстоит встретиться при установлении основных закономерностей в распространении волн в упругих анизотропных средах. Подобные затруднения усугубляются вследствие существенно большего разнообразия и протекании волновых процессов, возбуждаемых в таких средах. Интенсивное развитие и применение в исследовании волновых процессов получили асимптотические методы. Наиболее известным является лучевой метод, предложенный В.М. Бабичем и получившим развитие в его работах с Булдаревым В.С., Молотковым И.А. и др. [75, 76]. Применение различных численных и приближенных методов описаны в работах [77, 78, 79]. Анализ литературы, посвященный изучению волновых процессов в анизотропных средах, показывает, что эти исследования ограничивались распространением волн вдоль особых направлений и построением индикатрис скоростей. В настоящее время широко известна эффективность матричных методов при исследовании волновых процессов в упругих средах. Впервые матричный метод был применен Thomson W. T. [80] для численного исследования волнового поля при отражении волн от системы однородных слоев, заключенных между жидкими полупространствами. При этом матричное уравнение, полученное для границ однородных слоев, Томсон обобщил для пачки слоев. В дальнейшем Haskell N. A. применил матричный метод для численного изучения закономерностей распространения упругих поверхностных волн в кристаллах [81]. Матричный метод при исследовании волновых процессов в анизотропных средах в основном применялся при изучении и численном анализе уравнений дисперсии волн, для численного решения высокосимметричных анизотропных средах, определения особых направлений. С матричным методом непосредственно связаны и другие подходы, которое проводилось Л.М. Бреховских [82] и Kennet B.L.N. [83]. В казахстанской научной школе академика Ержанова Ж.С. вопросы применения матричных методов к исследованию динамики неоднородных сред начали разрабатываться в конце 70-х годов [84 – 94]. Развивается аналитический метод, основанный на построении структуры матрицантов системы обыкновенных дифференциальных уравнений первого порядка с переменными коэффициентами, к которой сводятся исходные уравнения, описывающие динамику исследуемого волнового поля. Введения понятия структуры матрицанта и ее определение позволило распространить классические методы, развитые Бриллюэном и Пароди [64] для дискретных периодических структур, на сплошные периодически неоднородные среды, а также в два раза понизить степень характеристического уравнения, определяющего дисперсию волн, что несомненно, является одним из существенных достоинств и конструктивным отличием этого метода от других его модификаций. В настоящее время решение широкого круга теоретических и прикладных вопросов динамики сплошных сред требует более полного учета анизотропии и неоднородности физико-механических свойств. Главной особенностью анализа волновых процессов в анизотропных средах является принципиальная не применимость в этих задачах физических представлений и математического аппарата, разработанного для изотропных сред. Это связано с невозможностью разделения волнового поля на прямые и обратные волны. Другой существенной трудностью является обилие физико-механических параметров. Методом матрицанта рассмотрены задачи распространения волн [84, 95, 96] в упругих анизотропных, средах, электромагнитных, электроупругих, пьезоупругих волн в анизотропных диэлектриках [97 – 103], волн в анизотропных термоупругих средах [104 – 111], волн в анизотропных диэлектических средах с магнитоэлектрическим эффектом [112, 113], изгибных волн в ортотропных пластинах [114, 115]. В зарубежных публикациях Тлеукенова С.К. [88, 91, 116 – 122], в частности была определена структура матрицантов уравнений движения неоднородных анизотропных сред. Эти публикации положили начало качественно новому уровню исследований динамики неоднородных сред с применением рассматриваемого метода и единообразному изучению закономерностей распространения волн различной по физической природы, в неоднородных и периодически неоднородных анизотропных средах. Основным, принципиальным достоинством метода матрицанта является единообразие описания волновых процессов при наличии нескольких физических эффектов: термоупругий, магнитоупругий, пьезоэлектрический и магнитоэлектрический, пьезомагнитный и магнитоэлектрический эффекты [123 – 130]. Актуальность темы. Широкое применение лазерного (электромагнитного) излучения в науке и технике требует знания ясной физической картины волновых процессов в самых разнообразных средах. Тема настоящей работы посвящена исследованию особенностей распространения электромагнитных волн в диэлектрических анизотропных средах с магнитоэлектрическим эффектом. Изучение закономерностей распространения электромагнитного излучения в средах с различными физическими свойствами позволяет анализировать оптические свойства различных систем, а так же конструировать устройства, управляющие различными характеристиками излучения. В связи со сказанным, развитие и применение аналитических методов исследования, а также формирование представлений о поведении электромагнитных волн в анизотропных средах с учетом магнитоэлектрического эффекта являются актуальным. Научная новизна. Научная новизна работы заключается в приложении метода матрицанта к изучению распространения электромагнитных волн в анизотропных средах с магнитоэлектрическим эффектом; получении инвариантных соотношений, имеющих место в рассматриваемом процессе, и отражающие законы сохранения; матричной формулировки граничных условий; аналитическом решена задача отражения и преломления электромагнитных волн на границе изотропной среды и анизотропной среды с магнитоэлектрическим эффектом. Цель исследования. Целью работы является теоретическое изучение стационарных волновых решений уравнений Максвелла для анизотропных сред с магнитоэлектрическим эффектом методом матрицанта, разработанного профессором С. К. Тлеукеновым. Метод исследования. Метод исследования работы – аналитический, основанный на развитии матричных методов исследования динамики упругих слоистых сред. Суть метода заключается в приведении исходных уравнений Максвелла, на основе метода разделения переменных, к эквивалентной системе обыкновенных дифференциальных уравнений первого порядка с переменными коэффициентами и построении структуры матрицанта. Матричный метод позволяет при едином подходе рассматривать распространение волн в широком классе сред. Другое достоинство этого метода состоит в том, что выражения, полученные матричным методом, имеют весьма компактную форму, которая оказывается удобной как при аналитических исследованиях, так и при численных расчетах. Объект исследования. Объектом исследования работы является распространение монохроматических электромагнитных волн в анизотропных диэлектрических средах с магнитоэлектрическим эффектом тетрагональной, тригональной и гексагональной сингоний. Изучение закономерностей распространения электромагнитных волн основано на: - исследовании структуры матриц коэффициентов, описывающих распространение электромагнитных волн вдоль оси Z анизотропных средах с магнитоэлектрическим эффектом тетрагональной, тригональной и гексагональной сингоний; - определении структуры матрицантов в зависимости от структуры матриц коэффициентов; - исследовании распространения волн в периодически неоднородных средах, основанный на аналитическом представлении матрицанта; - построении уравнений дисперсии электромагнитных волн в случае неограниченной периодически неоднородной анизотропной среды с магнитоэлектрическим эффектом; - решении задача отражения и преломления электромагнитных волн на границе изотропной среды и анизотропной среды с магнитоэлектрическим эффектом. Теоретическая и практическая значимость исследования. Структура фундаментальных решений и явный вид аналитических представлений матрицанта позволяет исследовать распространение электромагнитных волн в однородных и периодически неоднородных анизотропных средах. Результаты, полученные в работе могут быть применены в теоретических расчетах при проектировании и изготовлении различных приборов и устройств.