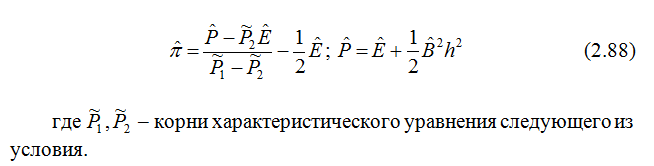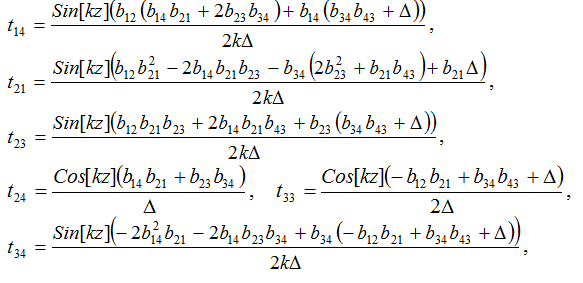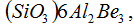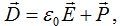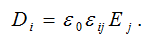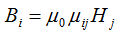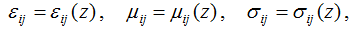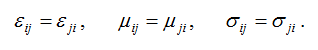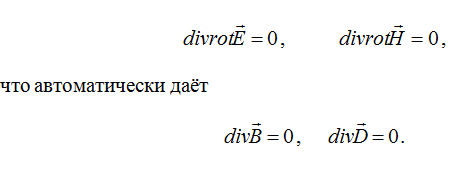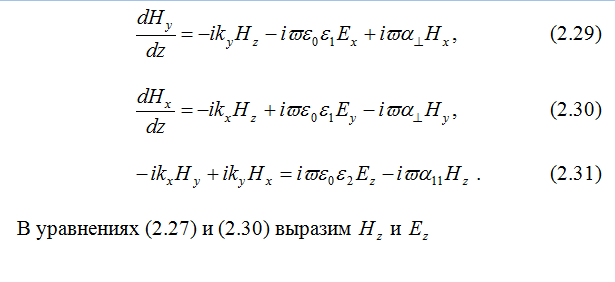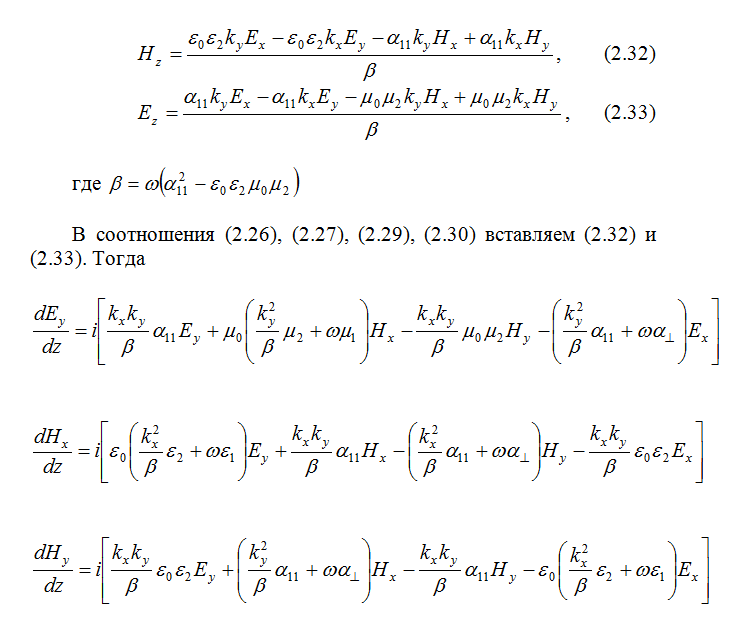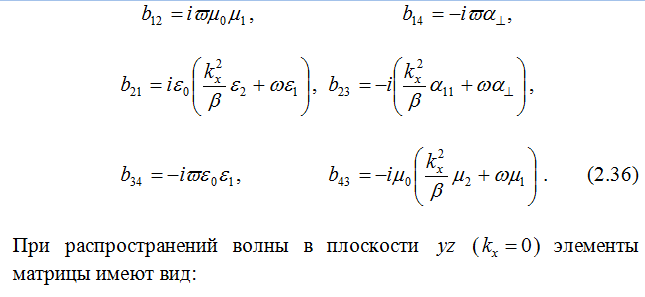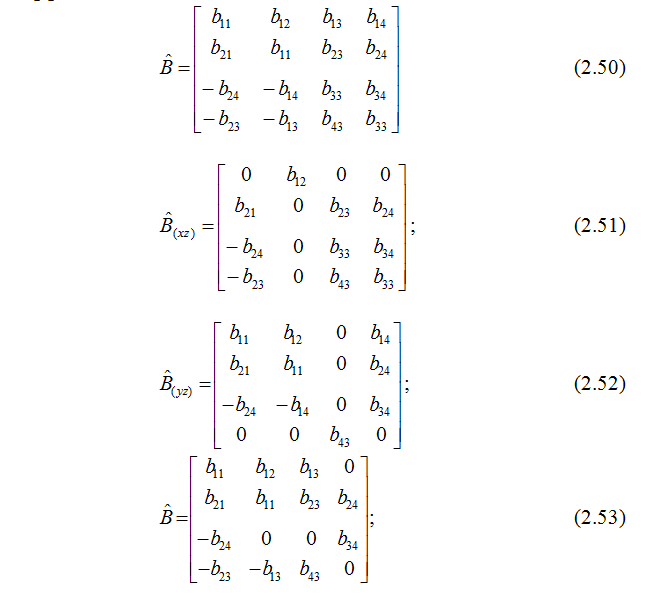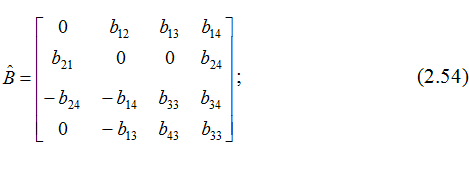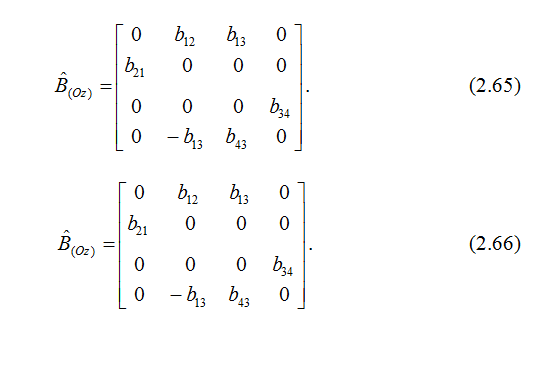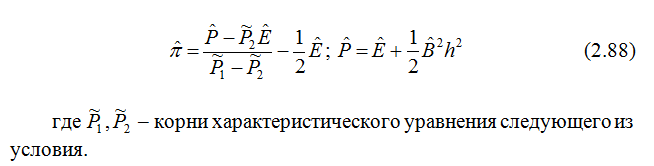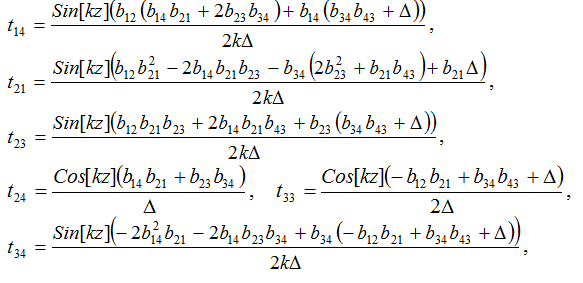2 Ресурсосбережение и ресурсопроизводство в отраслях экономики

2.1 Симметрия кристаллов Твёрдые тела (монокристаллы) отличаются анизотропией в своих свойствах. Иными словами свойства монокристалла различны в разных направлениях. В частности, поляризуемость кристалла, вообще говоря, не одинакова в разных направлениях. Анизотропия в свойствах монокристалла связана с характером его внутренней структуры, т. е. с наличием кристаллической решётки. Анизотропность среды может также создаваться наложением внешних полей: магнитных (эффект Коттона-Мутона), электрических (эффект Керра), упругих деформаций (впервые исследовали Зеебек и Брюстер). Анизотропия в полояризуемости кристалла проявляется, в частности, в том, что если вырезать из монокристалла две пластинки, различно ориентированные относительно кристаллографических осей, и поместить сначала одну, а затем и другую между обкладками конденсатора, то ёмкость конденсатора в обоих случаях, вообще говоря, не одинакова. Отсюда следует, что диэлектрическая проницаемость, а, следовательно, и диэлектрическая восприимчивость кристалла различны в разных направлениях. Исключение составляют кристаллы кубической сингонии, которые ведут себя как изотропные тела. Если взять, например, кристалл берилла

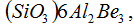
принадлежащего к гексагональной системе, то его диэлектрическая проницаемость равна 7,44 и 7,85 в зависимости от того, параллельно или перпендикулярно электрическое поле оси шестого порядка. Для апатита диэлектрическая проницаемость при поле, направленном вдоль оси, равна 7,4 , а при поле перпендикулярном оси равна 9,5. особенно велика разница в значениях диэлектрической проницаемости у рутила TiO₂ принадлежащего тетрагональной системе. Если поле направленно вдоль оси (4-го порядка) диэлектрическая проницаемость равна 173, если же поле направленно перпендикулярно оси, то диэлектрическая проницаемость равна 89. Анизотропия поляризуемости характерна для монокристалла. В поликристаллах, состоящих из большого числа маленьких кристаллитов, произвольно ориентированных друг относительно друга, происходит усреднение поляризуемости, и такие кристаллы ведут себя в электрическом поле как изотропные тела (газы, жидкости, аморфные тела). Анизотропия поляризуемости приводит к анизотропии диэлектрической проницаемости, т.к. электрическая индукция связана с поляризованностью и напряжённостью электрического поля соотношением:

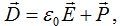
независимо от того изотропно тело или анизотропно. Из этого следует, что в слабых полях между векторами и имеет место линейная связь, но эти векторы, вообще говоря, не параллельны. Нумеруя координаты цифрами 1,2,3, можно представить эту связь в виде:

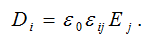
Для большинства веществ магнитная индукция является линейной функцией напряжённости поля вплоть до её очень больших значений, и только для ферромагнетиков линейная зависимость наблюдается при малой напряжённости поля и очень быстро сменяется сложной нелинейной зависимостью. Для монокристаллов векторы и не параллельны, хотя связь между ними по-прежнему считается линейной. В этом случае декартовы составляющие векторов и связаны между собой линейными соотношениями

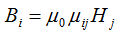
Тензор u_ij характеризует магнитные свойства вещества и называется тензором магнитной проницаемости. Если среда является проводящей, то к материальным уравнениям (2.1) и (2.2) необходимо добавить зависимость между плотностью тока и вектором напряжённости электрического поля (закон Ома):

Основной темой исследований настоящей работы является изучение фундаментальных свойств решений уравнений Максвелла, описывающих свободные электромагнитные поля в неподвижных анизотропных средах, с тензорными характеристиками, зависящими от одной из пространственных координат (координаты z). При этом функции

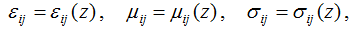
, в общем случае полагаются кусочно-непрерывными. Рассматривая проводящие среды, будем учитывать лишь наведённые токи. Объёмную плотность зарядов будем считать равной нулю ( ). Тензорные характеристики будем полагать симметричными, т.е.

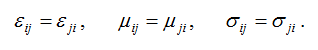
Анизотропные среды характеризуются обилием параметров. Одним из конструктивных путей преодоления этих трудностей является последовательное и детальное изучение свойств решений уравнений Максвелла в достаточно широком классе анизотропных сред с тем, чтобы установить закономерности этих решений от структуры тензорных величин, определяющих анизотропию среды. Естественно, что такое изучение целесообразно проводить на базе возможно более простых волн достаточно общей природы. В данном исследовании рассматриваются гармонически зависящие от времени решения уравнений Максвелла и метод разделения переменных относительно пространственных координат. С учётом высказанных выше исходных положений представление решений волновых полей рассматриваются в виде:

Исходной системой являются уравнения Максвелла (2.7) и материальные уравнения (2.1), (2.2), (2.3). При этом будем учитывать соотношения (2.5) и (2.6), а также отсутствие токов ( ). Указанная система уравнений требует некоторых уточнений и пояснений. Дело в том, что эта система состоит из 14 уравнений относительно 12 компонент электрических и магнитных полей. Кажущаяся переопределённость системы связана с тем, что последние два уравнения в (2.7), в данном случае, является следствием первых двух. Действительно, взяв операцию дивергенции от левых частей первой пары уравнений (2.7), получим:

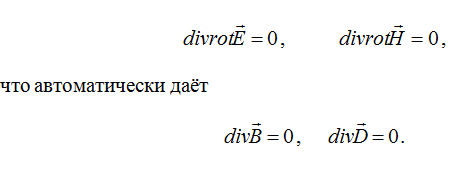
2.2 Тензорные характеристики При линейной зависимости между векторами и , из независимости второй производной от свободной энергии по компонентам вектора при неизменных значениях температуры и плотности следует симметричность компонентов тензора диэлектрической проницаемости:

2.3 Исходные соотношения и приведение их к системе уравнений в матричной форме Рассмотрим решение волновых полей в виде:

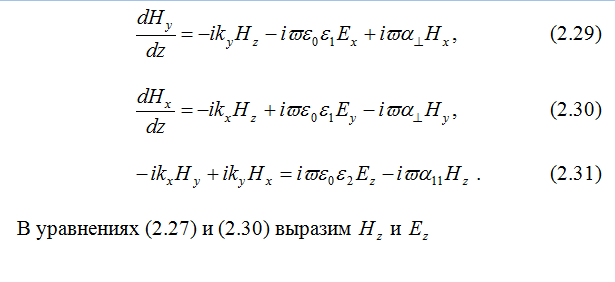
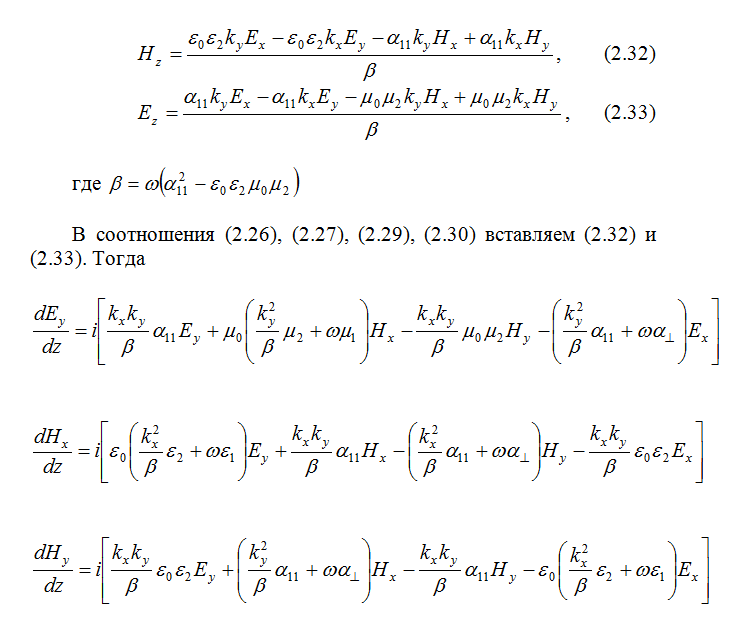
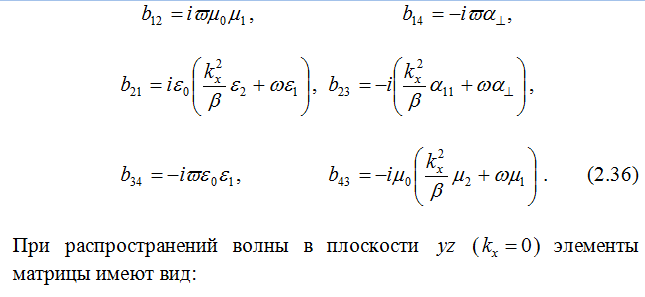
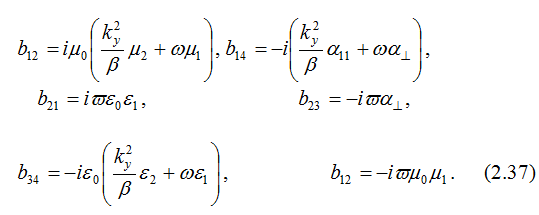
2.4 Структура матрицанта Как было выше сказано, уравнения Максвелла с учётом материальных уравнений приводятся к системе четырёх обыкновенных дифференциальных уравнений первого порядка:

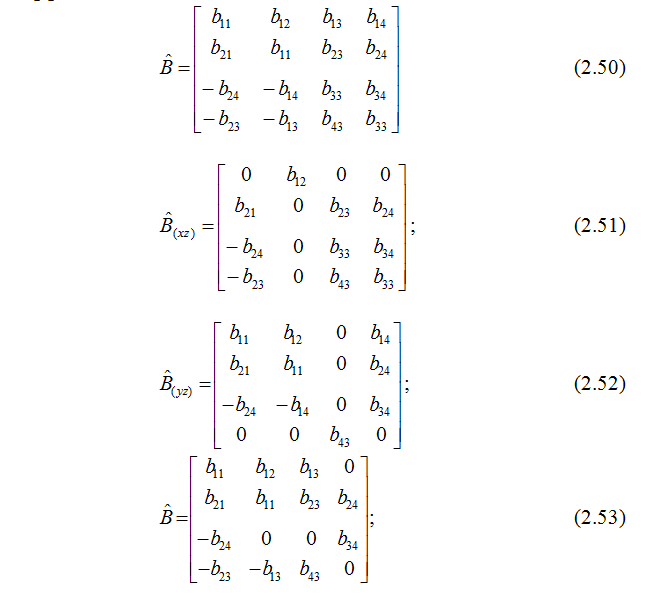
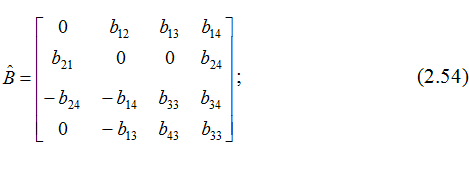
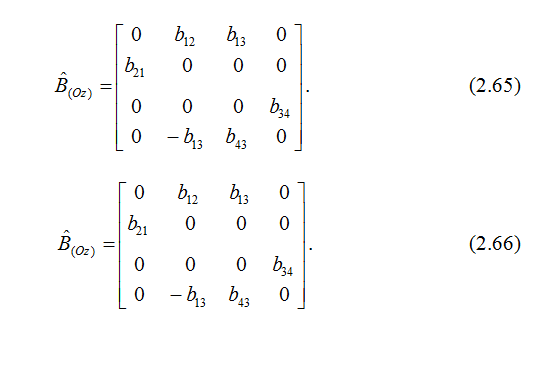
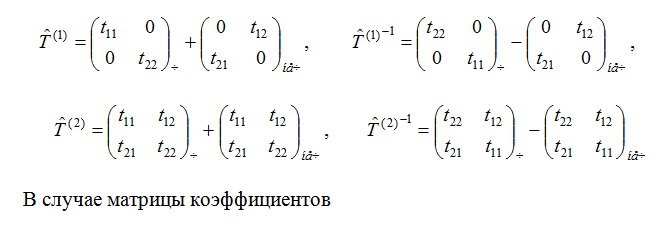
2.5 Матрицант однородной анизотропной среды В рамках метода матрицанта, усредненный матрицант, описывающий распространение электромагнитных волн в анизотропных средах с магнитоэлектрическим эффектом, имеет аналитическое представление: