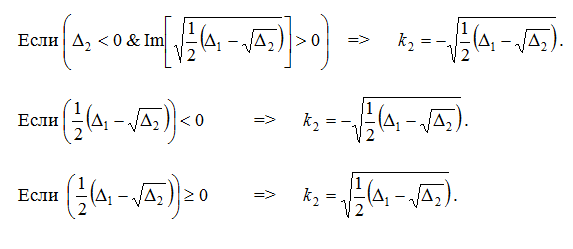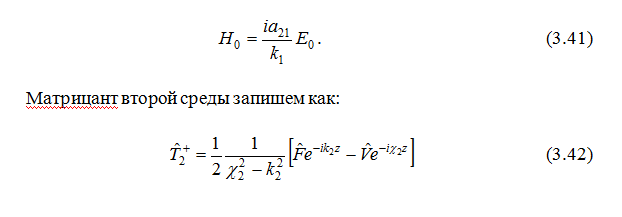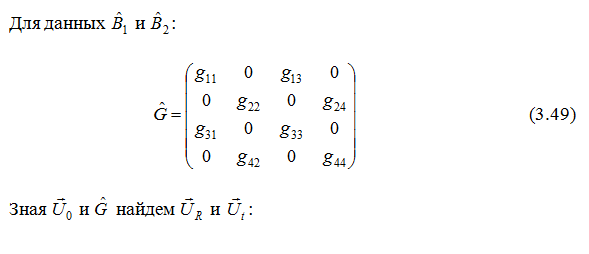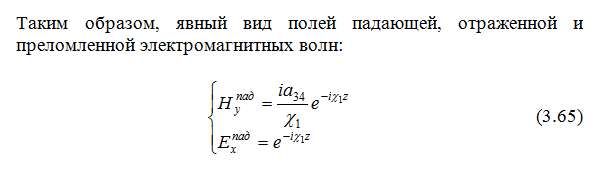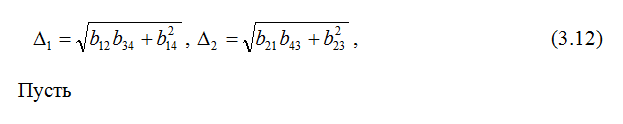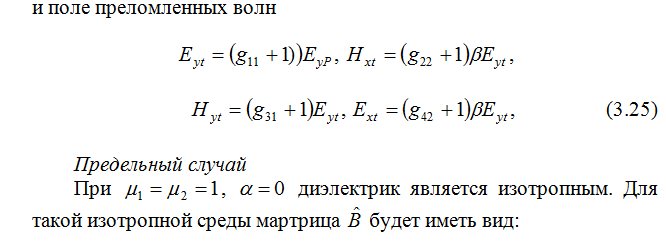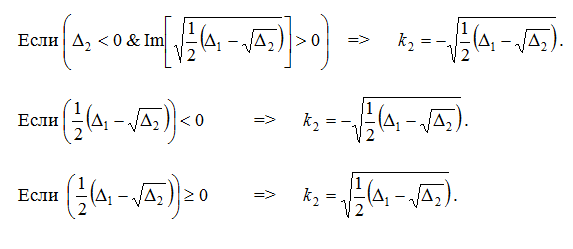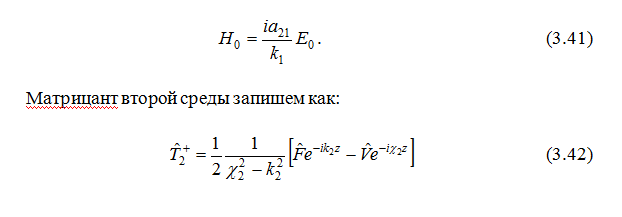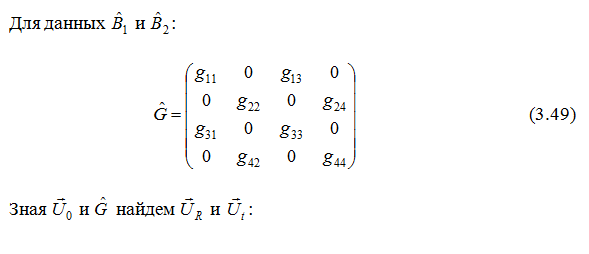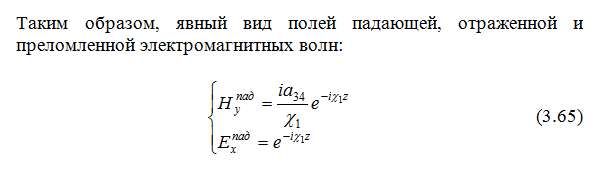3 Задача отражения и преломления электромагнитных волн на границе двух сред
3.1 Матричная форма граничных условий задач отражения и преломления электромагнитных волн.
Рассмотрим условия, накладываемые на волновые поля при взаимодействии волн с границей двух полупространств.При матрицанты (2.87) могут быть записаны в виде



3.2 Коэффициенты отражения и преломления электромагнитных волн на границе изотропного диэлектрика и анизотропного диэлектрика с магнитоэлектрическим эффектом
При двумерном распространении электромагнитных волн в анизотропных диэлектрических средах тетрагональной, тригональной и гексагональной сингонии с магнитоэлектрическим эффектом матрица, имеет вид (2.35) с коэффициентами (2.36) ( ) Вычисления на основе (3.8), с учетом выражении (2.9), позволяют получить явный вид матрицы :


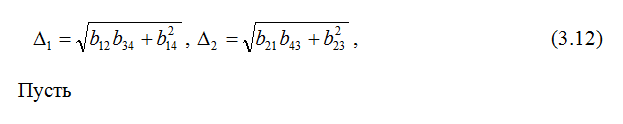



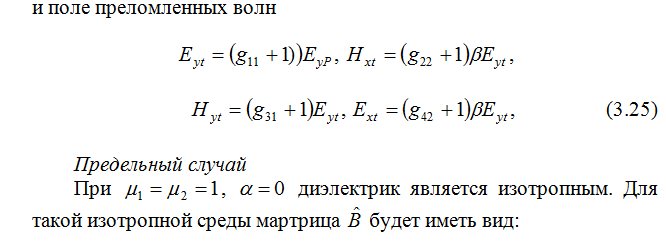



3.3 Энергетические коэффициенты отражения и преломления
В этом параграфе рассмотрим аналитические формулы потоков энергии при отражении и преломлении электромагнитных волн на границе раздела изотропного полупространства и анизотропной среды магнитоэлектрическим эффектом.
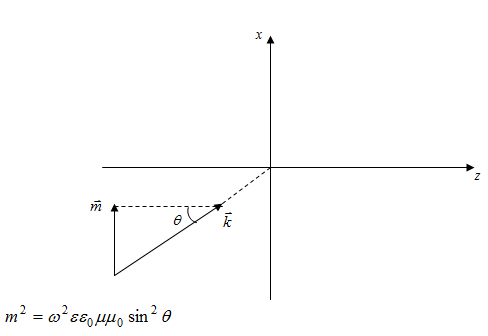
Пусть границей раздела сред является плоскость z=0. Анизотропную среду ориентируем таким образом, чтобы оси декартовой системы координат совпали с соответствующими кристаллографическими осями.
Отражение и преломление волн в случае падение на границу двух сред электромагнитной ТЕ волны.
Пусть на границу раздела из изотропной среды падает электромагнитная ТЕ волна, то есть вектор напряженности магнитного поля лежит в плоскости падения.
Матрицы коэффициентов изотропной среды и анизотропной среды с магнитоэлектрическим эффектом запишем как: