Проблемалық технология оқытуда ең бірінші қолданылатын тәсіл. Проблемалық оқыту – дидактикалық жүйе, студенттердің білім меңгеру іс-әрекетіндегі шығармашылық заңдары мен білім игерудегі тәсілдері мен әдістерінің негізіне жүгінетін нысан. Студенттердің шығармашыл қызметінің іс-әрекетін мыналарға негіздеп өткізген жөн:

-   шешімнің альтернативін табады;

- бұрынғы таныс шешімді жаңамен қоса біледі;

- нысанның құрылымын жіктей алады;

- белгілі бір стандартты жағдайда жаңа мәселені анықтайды;

- жаңа жағдайларға байланысты студенттер жаңа білім мен қабілетті өздігінен меңгереді;

- таныс нысанның қызметін жаңа қырынан көреді;

- бұрынғы өзіне мәлім шешімдерді нұсқалы тұрғыда құрастыра алады.

Кез-келген дидактикалық жүйе оқытудың арнаулы технология-сын іске асырады. Оның құрылымын, табысын жобалайды, (проекті) алгоритмге салады, оқу материалын өзінің ақиқатына айналдырады, педагогикалық өзара байланысқа түседі. Проблемалық оқыту технологиясы – бұл арнайы құрылған амалдар мен тәсілдердің жиыны. Мұның өзі әр студенттің өздігінен қарама-қайшылыққа келіп тұрған мәселенің шешімін табуға ынталандырады. Сөйтіп, олардың когнитивті танымдық қызметінің дамуына түрткі жасайды. Аталған таныс емес мәселенің шешіміне оқытушы-профессор құрамы арнайы үлгілерді студенттер назарына ұсынады. Соған нысанды шешу тапсырмасы беріледі. Бүгінгі таңға дейін: «проблемалық оқыту инновациялық технологияға жата ма?» – деген сауал қойылып келеді. Оның жауабы сонау кеңестік дәуірлерде И. Лернерден бастап беріліп келе жатқанын ескерген жөн. Кеңестік дәуірде тек дәстүрлі оқыту ғана басымдықта болды деу жаңсақтық пікірге апарады. Сол кездің өзінде дамытпалы оқыту мен проблемалық оқыту мәселелерінің шешімдерін тапқан талай инновациялар бар екені бүгінгі педагогика тарихынан мәлім. Басты ерекшелігі: материал әрі тереңдікте, әрі тұрақты, әрі қарымды меңгеріледі. Студенттер білуге тиісті білім мазмұнын қызыға меңгеруге ынталы болады. Аталған іс-әрекет – проблемалық оқытудың басымдықтағы мақсат-мүддесі. Проблемалық оқытудың технология сапасына өтуі – жуырда болған жаңалық.

Мәселені шешу, қарама-қайшылықты табу, өзектілігін дәлелдеу – педагогика ғылымының бөлінбес бір маңызды тұсы. Бірақ барлық өтілетін сабақтарды проблемалық нысан деп айтуға болмайды. Оның негізгісі - білім мазмұнындағы мәселелердің шиеленісі мен оны шешу үдерісінде қолданылатын ең ұтымды тәсілдердің жиыны. Проблемалық оқытудың құрылымы төмендегі әдіснамалық тәсілдерден тұрады-(зерттеуге қатысты нысанды өзектендіру, проблемалық ситуация туғызу, оқу мәселесін шығару, проблемалық мүмкіндіктерді түзу, мәселе шешімін парасатты іс-әрекетпен табу (зерттеудің болжамын құру, оны дәйекті фактілермен дәлелдеу, әрбір болжамның іздерін жинақтау), проблема шешімін тексеру және оны қайталау.

Студенттердің когнитивті танымын оқытушы-профессорлар құрамы арнайы әдістеме негізінде зерттесе, онда ол іс-әрекетті гносеологияға жатқызамыз, яғни әр студенттік болмысындағы когнитивтік танымның қисынын дәл табу дегенді білдіреді.

«Проблемалық жағдай», «Оқу мәселесі» және «Проблемалық міндеттер» аталған технологияның негізгі қолданатын ұғымдары, тірек сөздері. Проблемалық жағдай – тұлғаның белгілі бір оқу іс-әрекетіндегі бастан кешірген қиын сәті, оны шешудің жаңа жолдарын тауып, біліктілікті жаңарту ізденісі мен зерттеу бағытындағы жаңа тәсілдердің тууы. Проблемалық  жағдай – ойлау, бағамдау іс-әрекетінің таусылмас қайнар көзі. Бірақ бұндай түйінді сөзді барлық педагогикалық қиындық туғызған нысанды ойлау қабілетін танытады деген сыңайда қабылдамаған орынды. Әу баста студенттің қарастыратын мәселесіне тиісті білім қоймасы жоқ болса, онда ешқандай проблемалық жағдайдың парасатты іс-әрекетке әсері бар деу жаңсақтыққа апарады. Мұнан басқа, проблемалық жағдайының тууына мыналар себеп болады:

- теориялық білімді тәжірибеде қолдану мүмкіндігінің шектеулілігін түсінгенде;

- қарама-қайшылықты шешуде тәжірибелік қабілеті жетілгенмен, теориялық біліктілігінің жетімсіздігін байқағанда;

- жаңа тәжірибе барысында студент өзінің бұрынғы меңгерген білім қорын пайдаланудың қажеттілігін түсінген жағдайда;

- егер студент қойылған міндеттерді шешудің тәсілдерін білмегенде және оған жаңа фактімен негіздеме бере алмағанда, мұны шешуге бұрынғы білімнің кәдеге жарамағанын байыптағанда.

Проблемалық  оқу мәселесі – бұл іздену тәжірибесінің қалануы, оқу мәселесін зерделеу, зерттеу іс-әрекетін қамтамасыз ету мақсатында қойылған сұрақтар жиыны. Шешімнің асырылады. Проблемалық міндет – оқу мәселесін шешуді көздейтін нысан. (Егер мұндай сұрақ бұрын студенттерге таныс болмаса, проблемалық міндетке жатады). Проблемалық міндетке студенттердің шығармашыл ойлау мүмкіндігі төмендегілерді іске асырады:

- жобалы теориялық және тәжірибелік іс-әрекет сапасында тексереді;

- танымдық проблеманы шешудің нұсқаларын ұсынады және болжамын айтуға ынталандырады;

-  танымдық деңгейді құрастырады.

Проблемалық оқытудың әдістері оқытудың мәселесін шешуге жағдай жасайды. Оқыту мен оқу мәселесін қарастырады. Оқытудың мәселесі студенттердің іс-әрекетін алдын-ала қарастырылған мәселенің шешімін жүйемен табудың шарттылығын қамтамасыз ету тұрғысында ұйымдастырылады. Проблемалық оқу студенттердің қызметі шығармашылық бейімділікте ұйымдасуының тәсіл-амалдарына талдау жасау тұрғысында өткізіледі. Болжамды шешудің негіздері мен дәлелдері айқындалады. Педагогикалық тәжірибеде проблемалық оқытудың үш түрлі әдістері іс-әрекет жүйесіне тірек болады:

- ізденістілік;

- оқу материалын проблемалық деңгейде ұсыну;

- зерттеушілік.

Оқу материалын проблемалық маңызда ұсыну әр студенттің ғылыми түсінігін оятып, шындықтың жүзін айқындауына мүмкіндіктер туады. Студенттердің ішкі қайшылығын туғызып, оған нақтылы да нұсқалы жауап табуға қолайлы жағдай туғызады. Проблемалық оқытудың негізі – оқу материалын бинарлық үдерісте жіктеп алу. Оқытушы-профессорлардың  іс-әрекеті (оқылуға тиісті материалды өзектендіру, міндеттерді жіктеу, проблемалық жағдай құру, оқу мәселесін түзу, ішкі қайшылықты ашу, болжамды талқылау, оның шешімін дәлелдеп айтып беру, сараптау алаңын дәлелдеу, қорытындыны жіктеу және жинақтау).

Ізденістік әдісте студенттер өздерінің өздік жұмыстарының жемісін оқытушы-профессордың басшылығымен іске асырады.

Оқытушы-профессорлардың  іс-әрекеті (проблемалық ситуация тудырады, проблема және проблемалық қадамдардың шешімін жоспарлайды, ізденістен кейін қадамдарды шектейді, қорытынды жасайды, студенттерге сұрақтар даярлап, тапсырмалар береді, нұсқаулықтар жасайды). Оқытушы-профессорлардың проблемалық мазмұнда оқытуды бинарлық үдерісте құруы жоғарыда берілген түрде дамиды.

Студенттердің проблемалық мазмұнда оқу үдерісін бинарлы сипатта құруының мүмкіндігі (бұрынғы меңгерген білімін қайта жаңғырту, мақсатты түйсіну, мәселені ұғу, логикалық жүйемен құрылған мазмұнды тыңдау және оны қайталап айтып беру, оқытушы-профессордың кейбір сұрақтарына жауап беру, эксперимент нәтижесіне тілектес болу, кейбір жаңа қадамдарға риза болушылық, байқау, фактілерді еске сақтау, қорытынды шығару).

Ал ізденісті әдістерді бинарлық іс-әрекетте ұтымды пайдалану студенттердің іс-әрекетте тікелей байланысты. Бинарлық ізденісті іс-әрекетті студенттердің нәтижеге бағдарлауы үшін төмендегілерді ескерген жөн (проблемалық ситуацияны қабылдайды, проблеманы ұғады,  оның міндетін шешеді, негіздемесін ұсынады, тексерудің жоспарын құрайды, міндеттерін шешеді, қорыту, тұжырымдауға үлес қосады, зерттеушінің сұрақтарына жауап беріп, міндеттерін шешеді). ХХІ ғасырда білім мен ғылым саласындағы өзгерістер жоғары оқу орындарында оқытудың әдіснамалық ұстаным-бағыттарына жаңа міндеттер қойып отыр. Осыған орай, жоғары оқу орындарында оқытудың ұлттық сипатын әлемдік кеңістікке бейімдеп алу, жалпы ғаламдық ізденімпаздық танымды ойлау, пайымдау, парасаттау іс-әрекетін дамыту, студенттердің өздігінен тұжырым жасауға, олардың болашақ меңгеруге тиісті ғылым жетістігін сұрыптауға мүмкіндік туғызу бүгінгі өзекті мәселе болып отыр. Себебі, жоғары оқу орны білімді, интеллектуалды әлеуетті қоғам ғана өркениетті экономикалық, әлеуметтік және де қарқынды дамудың көшбасшысы бола алады. Аталған көкейкесті мәселені шешу үшін бүгінгі таңда жоғары мектеп дидактикасының әдіснамалық бағытын, оның мәнін, мазмұнын жаңаша ғылыми-педагогикалық тұрғыдан қарастыруды қажет етіп отыр. Әдіснамалық бағыт жоғары оқу орындарында өзекті мәселелердің тіректік шоғырының сипатын және оның негізгілерін жинақтап алу іскерлігінен туады. Өзекті мәселелердің тіректік шоғыры дегеніміз – бүгінгі модернизация кеңістігіне қатысты оқытудың кредиттік жүйесін жан-жақты меңгеру. Алдымен оның әдіснамалық негіздерін мемлекеттік стандарт шеңберінен іздеу көзделеді. Оның тірегі – типтік бағдарлама, ал оның тірегі типтік жоспар, оның тірегі – оқытушы-профессор құрамының жұмыс бағдарламасы. Жіктемемен берілген өзекті мәселелердің тіректік шоғыры тек сандық көрсеткіштермен шектелмейді. Мәселен, сәулет-құрылыс факультетінің міндетті құрамына кіретін «Инженерлік сызба» пәнінен  мемлекеттік типтік бағдарламасы бойынша 90 сағат берілген.

Өзекті мәселенің біріншісі осы берілген сағатқа орай стандарт шеңберінде ұсынылған бағыттарды тіректік бағдарға алуға тиіс. Нақтылап айтсақ, төмендегідей түзілімдер шоғырланып беріледі:

- сызықтық перспективаларды геометриялық негіздері;

- инженерлік сызба туралы түсінік;

- кешенді сызбадағы көлеңке және оны құрудың жолдары;

- аксонометриялық сызбадағы көлеңке;

- сызықтық перспективалардың позициялық және өлшемдік есептері.

- қисық сызықтар және беттердің перспективалары;

- перспективалық бейнелерді құрудың негізгі әдіс-тәсілдері;

- сандық белгісі бар проекциялар және т.б.

Аталған сегіз макроблоктардың ғылыми-әдіснамалық бағыттары типтік бағдарламаларда берілген міндетті әдебиеттер мен қосымша әдебиеттер түзілімін оқытушылық нысанада ұстап, ұсынылған білім мазмұнының оқытушы ұғымына қиындық келтірер ұғымдардың шешілуіне қатысты сұрыпталады. Ұғым дегеніміз «Инженерлік сызба» пәнін оқыту барысында қолданылатын терминдердің қазақша баламасын табу және оның сөйлем, сөз тіркестеріндегі, жалпы мәтін құрылымындағы мәнін, алатын орнын, маңызын, бүгінгі сәулет өнеріне қатыстылығын түйсінуге бағдарлау. «Инженерлік сызба»  пәнінің стандарт ұсынған макроблоктарының ішіндегі ең үлкен ғылыми жүйелерін шоғырландырып алғаннан кейін, оған қосымша құрамдық мәніндегі біліми нысандарды ажырату мақсатында аталған жеке жіктемелерді тұтастықта қарау кредитті есептеуге мүмкіндік жасайды. Міне, осындай оқыту іс-әрекетінен әдіснамалық бағыт сараланып шығады. Оның жүйесі төмендегідей болып келеді:

-  «Инженерлік сызба» пәнінің  ғылымаралық, интеграциялық мүмкіндігін саралау және студенттердің пән меңгеру үдерісіндегі болашақ кәсіби мамандығын игеруге ғылыми негізде құлшынысын ояту, оны қызықтыру, ұлттық ерекшеліктерін ескеріп, олардың ішкі білімдену қарқынын, ішкі интеллектуалды әлеуетін іске қосу шеберлігін өздігінен ұштауға бағдарлау;

- «Инженерлік сызба» пәнінің  ғылым мен білім кеңістігіндегі атқаратын қызметін анықтау.

- ғылыми-біліми іс-әрекетінің тұтастығын қамтамасыз ету мақсатындағы ұтымды технологияларды таңдау (мемлекеттік тұжырымдама, мемлекеттік стандарт, бағдарлама, оқулықтар, оқу құралдары, жұмыс жоспары және т.б.;

- негізгі ұстанымдарды айқындау, педагогикалық ғылымның даму әлеуетін жіктеу;

- оқыту үдерісіне қатысты жоғары оқу орнына педагогиканың негізгі әдіснамалық талаптарының жүйесін шығару.

Оқытушы «Инженерлік сызба» пәнінің ғылыми негізін сұрыптап, оның зерттелу құрылымын инновациялық пайыммен талдауға міндетті. «Инженерлік сызба» пәні  тек сызбадан тұратын сипатында оқылмай, оның сызбалары өмір салтанатына тіректік, тіршілікке баған сапасында өтілуі оның өміршеңдігін қамтамасыз етеді. Микроблокпен берілген оқыту материалдары, нақтылап айтсақ, білім мазмұны кредиттік жүйемен оқытылғанда, силлабусқа жіктеледі. Силлабусқа жіктелу заңдылығы микроблоктардың ішкі құрамдарының сипатына бағынысты болып келеді. Егер оқытушы ұсынылған сегіз микроблоктың әрқайсысының кіші құрамдық жүйелерін мемлекеттік стандарт пен типтік бағдарлама талаптарына сай шығара алмаса, онда оқу бағдарламасының іске аспағандығы. Силлабустың ішкі құрам бөліктері алдымен жеке-жеке түзілімінде ұсынылады, бірақ оның тұтастық жүйелері кредиттік нысанға бағынысты. Аталған ішкі құрам бөліктері шкалаға жіктеліп, зерттеу сұрақтарына айналғанда ол рейтингіні құрайды. Сөйтіп, бір микроблоктан 8 түзілім таралып, ал оның әрқайсысы тағы бірнеше кіші құрам-шкалаға бөлінеді. Көріп отырғанымыздай, оқытушы қанша пәннен дәріс жүргізсе, сонша оның өзекті мәселесінің шоғыры бар деген қорытындыға келдік. Әр студент аталған силлабус талабын орындау бағытында алдымен міндетті әдебиеттерден қажеттісін бөліп алуы үшін оқушының дәрістегі нұсқаулық бағдарын басшылыққа алады. Нұсқаулық бағдар дегеніміз – студенттің аудиториядан тыс өздігінен жұмысын 70 пайыз ауқымында орындау мақсатына қатысты микроблоктық негізгі тілектік нысандарын айқындап беруі. Жұмыстың мұндай түрі тек дәріс арқылы 30 пайыз мөлшерінде сығымдалып, қарқынды мәнде ұсынылады. Нұсқаулық нысанды, бағдарды мемлекеттік стандарт арқылы жобалап алған оқытушы өзінің ғылыми-біліми үдерісіне логикалы тұрғыда бағындырып, студенттерге жаңа ақпаратты мемлекет ұстанымына үндестіріп, білімдену технологиясына сәйкес ұсынуы көзделеді. Студенттерді оқытуда әдіснамалық бағыттың екі дәрісі қабаттасып өмір сүріп келеді. Оның біріншісі – жоғары оқу орнында педагогикалық технология, ал екіншісі – білімдену технологиясы. Анықтап айтсақ студенттің ойлау, пайымдау, парасаттау іс-әрекеті оқытушының жоспарлап (мүмкін ойша құрастырып келген) келгеннен басқаша болса, оның бағасын кемітіп, тіпті сессиядан сессияға қалдырып ақыры студенттің тұлғалық кейпін бұзып, оқу орнынан оны шығаруға да қарсы еместік байқалып қалады.

Сөйтіп, педагогикалық технология ауқымында білімді интеллектуалды әлеует дамыту сыңайында қабылдауға толық қолайлы жағдай жасалмайтыны байқалды. Ішкі интеллектуалды әлеуетті дамытудағы оқытушының логикалық парасатты іс-әрекеті гносеологиялық дәрежеге ынталандырады. Егер оқытушы гносеологиялық деңгейді дамытуға бағыт алса, онда студенттер оқытушының нұсқаулықта ұсынған зерттеу іс-әрекетін одан әрі сабақтастықта алып кетуіне, жалғасын табуға ықыластанады. Сөйтіп студент өзекті мәселелердің төмендегідей магистралды бағыттарын бөліп қарастырады:

- «Инженерлік сызба» пәніне қатысты өндірісте қолданылатын жаңа ұғымдарға, терминдерге талдау жасап, оны жүйелейді, нақтылайды;

- сәулет құрылысының теориялық негізін стандарт деңгейінде зерделейді;

- пәнаралық байланысты, ғылымаралық, ұлттық және әлемдік кеңістіктегі интеграциялық әлеуетті сәулет өнерінің өркендеуіне ықпалын зерттейді;

- студенттер мамандығының салалық ерекшелігін ескеріп, олардың болашақ маман ретіндегі іскерлігін ширататын жаңа инновациялық білімдену технологиясын меңгерулеріне қолайлы жағдай туғызады;

- меңгеруге тиісті ғылыми-біліми нысанның құрылымын тұтастықта қарастырады.

Білімдену технологиясының алғашқы деңгейі гносеологиядан басталады дедік, олай болса педагогикалық технология секілді репродуктивті әдіс-амал қолданылмайды. Менің зерттеу еңбегімде нәтижесінде байқағаным – репродуктивті амал әр оқытушының әзірлеп келген дәріс жазбасын студенттер бұлжытпай қайталап беруі. Қайталау бар жерде дамуға шектеушілік қойылады дегенді аңғартады. Ал гносеологиялық амал әр оқушының ғылымдағы қарастырып отырған мәселесіне орай себеп-салдарын тәжірибелік негізін шартты тұрғыда ашуы болып есептеледі. Оқытушы өзінің ұсынып отырған ғылымының меңгерілуіне қозғаушы күш боларлық себеп-салдарын шартты тұрғыда ашу мақсатында бірнеше негізгі және қосымша оқулықтарды зерттеп, оның басымдық маңызын бөліп алуға тиісті ғылыми нысанның жобасы тек бір ғана ой-тұжырым жасауына оқытушы жағдай туғызады. Егер оқытушы соңғы тұжырымның нүктесін өзі қойып қойса, студент оны қайталайды. Студент қайталау тәсілінен аулақ болсын десек, онда оқытушы бір тақырыптың бірнеше түрлі ғалымдардың зерттеуінен өткеніне тоқталып, оның шешімін студент еншісіне қалдырса, аталған гносеологиялық деңгей дамытылары сөзсіз. Гносеологиялық деңгейде студенттер бірнеше ғылыми зерделеулерді өздерінің пайым-парасаттарымен түйіндеп, оған өз дүниетанымдарын білдіреді. Олай болса, студент бірнеше ғылыми жетістіктердің бар екеніне көзі жетіп, оны бағамдау іс-әрекетіне бағдарлайды. Бұл зерттеушілік іс-әрекет студенттің дәрістен дәріске дейінгі, тәжірибешіліктен тәжірибешілікке дейінгі ой әлемінің инженерлік сызбасының тек бір бөлігі ретіндегі қызметін емес, оның сәулет – құрылысына пайдасының қандай екеніне көзі жетіп, оған кәсіптік қызығушылығы артады.

Айта кетер бір жәйт, гносеология деген ұғымның өзі –тұлғаның бір ғылымға қатысты зерттеу іс-әрекетінің таным теориясы, әлемді өзінің бағамдауы, білімдегі ғылымның шындығына жетудің өлшемі, көрсеткіші және оның ақиқаттығы. Білімдену технологиясының алғашқы деңгейі гносеология екеніне тоқталып өттік. Енді екінші деңгейі – аксиология. Аксиология деген сөз гректің құндылық және оқу немесе сөз дегенді білдіреді. Былайша айтқанда, аксиология – құндылық табиғатын зерттейтін философиялық ұғым.

Сәулет құрылысында құндылық табиғаты – ол ұлттық нақышпен берілген бұрынғы нұсқаулы ғимараттардың үлгілерін зерделеу. Қазақ халқының, түркі жұртының ата дәстүрінде шеңбер сипатындағы құрылыстар орын алғаны белгілі. Ал ХХ ғасырда тік бұрышты үй құрылыстары белең алғаны бәрімізге аян. Міне, осындай ерекшеліктердің басты себептерін ашу – «Инженерлік сызба» пәнің  оқу үдерісіндегі жол-жөнекей шешілетін философиялық тәсіл. Дөңгелек, шеңбер түркі жұртының ұғымында күннің нұрын, бақыттың көзін, құттың жолын берсін деген тотемдік тұрғыдағы ұстанымдармен байланысты екені бүгінгі зерттеу еңбектерінен байқалды. Міне, осындай ата дәстүріндегі бағыттарды қайта жаңғырту бүгінгі сәулет-құрылысының құндылық табиғатына философиялық тұрғыда зердемен қарау дегенді аңғартады. Білімдену технологиясындағы деңгейлер одан әрі ғылыми ауқымда күрделене береді. Жалпы білім беру технологиясы – оқу үдерісін бүгінгі заман талабына, мемлекеттік стандарт ауқымындағы мемлекеттік сұраным шеңберінде жоспарлау, студенттердің типтік бағдарлама ұстанымына сай біліктілігі мен интеллектуалды әлеуеттерін тәжірибешілік, зертханалық, өздігінен жұмыстар арқылы дамыту, оны компьютерлік тесті жүйесімен тексеру, өзін-өзі тексеруі, студенттің өзінің тұлғалық болмысын меңгеруге тиісті мамандығына бағдарлай алуын дамытуға қолайлы жағдай жасау. Аталған гносеологиялық және аксиологиялық деңгейліктердің алдында (нөлдік деңгей) келетін деңгей – эвристикалық болып табылады.

Эвристикалық бұл үлкен проблемалы-зерттеу тәсілінің алдыңғы басқышы. Деңгейліктер жайлы (тәжірибелік білім) ой-тұжырымдар сан-салалы. Деңгейліктерді тек Блум мен Беспалько өлшемдіктерімен қарастыру – модернизация заңдылығын тежеу дейміз. Себебі деңгейлікті не 6, не 7 деп айту тек оқытушыны схематизмге апарады. Әр оқытушы өзінің кредиті мен силлабусын аталған мемлекеттік құжаттарды іске асыру тұрғысында қанша деңгейлктерге жіктей алса, ол деңгеліктер саны сонша болмақ. Деңгейлік тұрған жерде міндетті түрде әдістер қатар қолданылады. Оқытудың әдіснамалық бағыттары аталған жүйелердің нақты ғылыми-біліми нысандарынан туындайды. Эвристикалық деңгейі жоқ студент гносеология мен аксиологиялық деңгейге шыға алмайды. Міне, осындай бағыттарды ескеріп, жоғары оқу орындарында білімдену технологиясының тағы бір басымдық маңызы стохастикалық парадигма жинақы нәтижелерге жеткізеді.

Қорыта келгенде, педагогикалық технология жоғары оқу орындарында бүгінгі күннің нысаны еместігі. Жалпы техникалық бағыттағы мамандықтарда дәріс өткізу білімденудің жаңа инновациялары қарқындықпен дамуы – болашақтағы өркениетті елдер санатына қосылудың кепілі.

Студенттердің бүгінгі өмір талабына және әлемдік кеңістікте құзыреттілікке жетуі тек олардың жоғары оқу орындарында оқу және қабылдау, ой-өрісін дамыту секілді қасиеттерінің өркендеу қарқынына қатысты болып отыр. «Оқыту» деген ұғым тек іс-әрекеттің жиыны еместігін ескерген орынды. Себебі іс-әрекет белгілі бір заңдылықтар мен қағидаларға, білім мазмұнына бағынбаған тұста өнімсіз өзара әрекеттікті іске асырады. Сондықтан жоғары оқу орындарында дәріс және тәжірибешілік жұмыс жүргізетін кез келген оқытушылар және т.б. тұлғалар студенттермен іс-әрекетке түскен тұста оның ішкі жағдайларына толықтай дерлік ден қоюы көзделеді. Жалпы білім беретін және арнаулы білім меңгеретін мекемелер мен жоғары мектеп арасында айтарлықтай айырмашылықтар бар:

- оқу материалын, оқытудың дидактикалық негізінің жүйесін басқару, игерту тәсілі мен оның игерілуін тексеру тәсілін ұдайы өзгертіп отыру. Анықтап айтсақ, стандарт ауқымында студенттер дәріс, семинар,       зертханалық-тәжірибешілік, өздігінен жеке жұмыс түрлері сағатқа жіктеліп беріледі, ал мектепте әр ұстаздың шеберлігіне, кәсіптік құзыретіне қарай аталған сабақ түрлері өтіледі;

- мектепте көбінесе оқу, оқыту үдерісінен ұйымдастыруда әдіснамалық негіз құрастырылуы назардан тыс қалса, жоғары оқу орындарында бұл стандарт талабына сай жүргізілуі, ғылымилық заңдылығын жүзеге асырылуы бақыланады;

- мектепте күнделікті бақылау құрастырылса, жоғары оқу орындарында бақылау жұмысы, коллоквиум, семинар, сынақ, емтихан, тесті өткізу арқылы рейтинг жүйесімен бағаланады;

- жоғары оқу  орындарында өздігінен жұмыс мектептен әлдеқайда басым, атап айтсақ, 60–70 % көрсеткішке ие;

- мектепте мемлекеттік стандарт көлемінен шықпау қадағаланса, жоғары оқу орнында стандарт, типтік бағдарлама шегінен әжептәуір кең ауқымда меңгерілуі қадағаланады;

- мектепте ұстаз тұлға ретінде басымдықта болса, жоғары оқу орындарында оқытушы-профессор құрамының мәртебесі студенттермен     тепе-тең дәрежеде;

- жоғары оқу орындарында стандарттан тыс көптеген пәндер қамтылады. Мәселен, «Математиканы оқытудың әдістемесі», «Геометрияны оқытудың әдістемесі» және т.б.

- «Оқытушы – студент» арасындағы ықпалдастық сипаттың өзгеруі. Бұл өзгерістің мәні студенттің шәкірттен гөрі осы үдерістің көбірек субъектісі болып табылатын сипатында.

Салыстырмамен жүргізілген жоғары мектеп пен білім беру нысандарының арасындағы 8 айырмашылық екі мекеменің атқарар рөлін айқындап берерлік басты көрсеткіші дер едік. Байқап отырғанымыздай, мектеп жоғары оқу орындарында стандартқа жүгіну, оның ғылымилық негізіне өтілуге тиісті нысаналарды ыңғайлап отыру сияқты іс-әрекеттердің технологиясын меңгеру тәсілдері оқытушы-профессорлардың құзыреттілігіне тікелей байланысты екеніне көз жеткізеді. Бүгінгі модернизация кеңістігінде жоғары оқу орындарында оқыту үдерісі білімдену технологиясының негізінде өтілуін көздейді. Кредиттік технологиясының ұтысы – ақпарат тоғынынан ең қажеттісін жүйелеп, саралап, меңгеруге бағдарлауы. Кредиттік технологияға көшу үшін силлабустық жүйені әр оқытушы парасатты тұрғыда меңгеріп, оны тақырып ішіндегі негізгі және көмекші ұғымдарға жіктей білу шеберлігімен қарулану дәрежесінде іске асырылады. Олай болса, бүгінгі айтып жүрген оқытудың интерактивті технологиясын меңгермеген оқытушы силлабус құра алмайтыны түсінікті. «Интерактивті» деген ұғым екі сөзден құралады. «Интер» (ағылшын тілінде – интер ) – өзара әрекет, бір-біріне интелектуалды әлеует деңгейліктері орайлас келіп, екеуара, немесе одан да көп тұлғалардың ішінара түсіністікте тіл табыса алуы дегенді білдіреді.Бұл күрделі сөздің бір бөлігі. Ал «актив» (латын тілінде – aktuvus ) –  заңды тұлға меншігіндегі рухани, ғылыми, біліми нысананы, мүлігі, игілігі, құты, дәулеті, құнды қағаздары, ақшалы қаржы және т.б. деген ұғымды білдіреді. Адақтап айтсақ, модернизация кеңістігінде, ғаламдасу үдерісінде белгілі бір тұлғаны өзіне тән ғылыми игілігі басқалардың да ғылыми игілігіне айналуға мүмкіндіктердің барлығы дегенді аңғартады. Жаңа қоғам өзгерісіне қарай тұлғалық болмыстың соны ой-тұжырымдары интеллектуалды құндылық деңгейінде есептеліп, оның құны ғылыми жобалар, байқаулар, гранттар, жүлделер арқылы авторларына ақшалай қаржы түрінде бағаланып отыр. Кеңестік дәуірде интеллектуалдық құндылық тек білім беру басшыларының үлесі болатын. Бүгінгі таңда ақиқатты ғылыми еңбекке бөгет болар тосқауылдың жоқтығы Тәуелсіз Қазақстанның қол жеткізген рухани жетістігі дер едік. Егеменді Қазақстанда өмір сүріп жатқан тұлғалардың экономикалық мәселелері олардың интеллектуалды әлеуеттерінің деңгейліктеріне тікелей бағынышты.

Қорыта келгенде, «актив» әр адамның экономикалық қажеттігі пайданың көзі ретінде жарататын қоғамдық байлықтың барлық түрлері. Олай болса, «интерактивті оқыту» деген ұғымның жоғары оқу орнына қатыстылығының басымдықта келуі - бүгінгі ғаламдасу үдерісіндегі отандық рухани - ғылыми әлеуеттің құнын арттырудың көзі. Берілген анықтаманы жоғары оқу орнында оқытушы-профессорлардың дәріс, семинар-тәжірибешілік, зертханалық, студенттердің өздігінен жұмысы сияқты іс-әрекет тұрғысында қарастырсақ, оқытушы-профессорлар құрамы мен студенттердің өзара интеллектуалды әлеует дәрежесінде түсінісіп, қауымдасып қызмет атқаруы дегенді аңғартады.

Ойымызды одан әрі дамыта түссек, интерактивтік технология білімдену технологиясының кеңістігіне жатады. Интерактивтік технология 1 оқытушының 15 студентпен бірнеше рет білім мазмұнына қатысты өзара интеллектуалды әлеует деңгейлестігінде түсіне отырып қарым-қатынаста болуына мүмкіндік береді. Бүгінгі таңда педагогикалық технология білім беру реформасының алғашқы кезеңіне үлес қосқанымен шектелетіні байқалады. «Инженерлік сызба» пәні бойынша кіріспе дәрісін өткізуінде инженерлік сызба білім жоғары оқу орындарында басқа пәндерді оқуға жол ашатын, кәсіпорында инженер жұмысын атқаруға осы пәнді оқуға қажетсінуін  қызығушылығын туғызу үшін дәлел беріледі. «Инженерлік сызба» пәні бойынша білім шығарылатын өнім сапасымен өзара байланысын сондай-ақ, мемлекеттің өндірістік дамыған деңгейін көрсететін айқын дәлелі ұсыналады.

Білімдену үдерісіндегі педагогикалық зерттеу білім жүйесінің дамыту мүмкіндіктері техникалық графикасына білім технологиясын іріктену мақсатында және білім нәтижесінің талдауында жатқаны дәлелденген. Жұмыс тәжірибесінде оны басып шығару үшін «Инженерлік сызба» пәнін оқытудағы оқысынан туған мақсатты шығару технологиясының негізі анықталады. Білім беру тәсілдерін рет-ретімен анықталап, (түсіндірме – иллюстрациялық, репродуктивті, проблемалық, бөлшекті бүтіндей, бүтінді бөлшектей зерттеу ) оның іс-әрекет кызметіндегі тиімділігі зерделенеді. Жұмыс барысында білім берудің үдерісінде бөлшек негізін құрайтын әдістерінің рет-реті, нысанмен және бұл мақсатты орындау құралдарымен жалғасады. Оқу барысында техникалық қана емес және статикалық оқу құралдары пайдаланылады: плакаттар, оқулықтар, оқу құралдары, негізгі әдебиеттер және т.б. Әдістер, құралдар және нысандар әртүрлі жылдамдықта өзара қиылыса алады, бірақ оқыту тәсілдерін өзара байланысудың негізгі тенденциясының сақталуында оқытушы өзіне тиесілі арнаулы технологиясын қолдана алады. Бұл оқыту технологиясы мықты алгоритмі болып, оқытушының шығармашылық қабілеті мен мүмкіндіктері шегін кеңейте алады. Бір айта кететін жай оқыту үдерісіндегі құрылған технологиялық алгоритм пәннің мақсатына қарай өзгерістерге түсіп отырады. Менің  енбегімде анықталған оқыту тәжірибиедегі білім беру және тәрбиелік мақсаттарды жүзеге асыру технологиясы нақты сабақтың үлгілерін шығаруға және оларды оқытуда жүзеге асыруға мұрша беріледі.

Оқыту жүйесінің тіршілік етуінде ойлау тіршілігі тәсілдерінің игерілуіне және жылдам қабылдау үшін ақпаратты қорытуға бағытталады, өйткені инженерлік сызба студенттерге жаңа пән, сондықтан ақпаратты өзектілеуіндегі және жаңа графикалық ақпаратты оқу мәселесінің шешілуі көп уақытты талап етеді, бірақ ойлау тіршілігінің және жұмыс тәсілдерін қарқынды пайдалану жағдайында ғана сапалы оқу үшін қысқартылуы мүмкін. Сондықтан дәріс үлгілерін жасағанда, тәрбиелеу және оқыту заңдылығының өзара байланысында анықталған тақырып бойынша нақты ақпаратты жеткізуді үлгілеу қарастырылады. Осы әрекеттестікті үйлесімді түрде ақпаратты қабылдау заңдылығына сәйкес мақсатты рет-ретімен жүзеге асыруды құрастырып ұйымдастыру көзделеді. Дәрісті дайындауда оның мақсаттары тақырыпқа сәйкес құрылып, жұмыстың құрылымы жасалады. Олар «Инженерлік сызба» пәніне оқытудың стратегиялық мақсаттарын талдауда, нақты материал дәрісін құру үдерісінде анықталады. Стратегия мемлекеттің стандарт негізінде жүзеге асырылады.Мақсаттарға сәйкес дәрістің үлгіленіп теріледі.

Мұнда материалдың теориялық негізінің жинақталуы, сұрыпталуы есептеледі: ақпаратты мінездемелегенде оның құрамы (элемент тізімдемесі – дәлелдері, заңдары, заңдылықтары) түзілуі, құрылымы (өнегелілік қарым-қатынас түріндегі элемент арасындағы өзара байланысы) және қызметі (ойлау тіршілігі тәсілі бойынша және оны басқаруды және оқыту тәсілі бойынша ақпаратты ұсыну динамикасы) жүзеге асырады.

Дәрісте оқылатын ақпаратты үлгілеуінде оқытушы студенттерге қандай дәлел, құру тәсілдеріне сызбалық тіршіліктің тәсілдерін және оларды қабылдауды ұйымдастыру тәсілін ойластыру жайлы ұсыныстар береді. Бұл ақпаратпен жұмыс істеу алгоритмі белгілі бір қатал тәртіпке бағынбай, жалпы реттілігін сақтауында құрамдық саны өзгере беретіні белгіленеді. Әрі қарай дәрісті құрастырғанда, бағдарламамен қарастырылған негізгі білімі, басты мәні, қайталану мәні, дәлелі, ақпараттар, ақпаратты қабылдауын ұйымдастыру үшін дәрісте қолданылатын ойлау, пайымдау өрістері анықталады.Дәрісте ақпаратты үлгілеуінде оқытушы нақты заттық ұғыммен сезімді анық байланыстыратын шекараға шығу мүмкіндіктерін есептеп, ақпаратты қорыту үлгісін жасайды: әртүрлі сезімді үлгісін байланыстыру және қосу; оларды түсінікті оймен өрнектеуін көрсетеді. Дәрістің аяқталуында оқытушы студенттерге дәріс теоретикалық материалын схема түрінде көшіруді студенттердің қалауы бойынша ұсынады (графикалық ақпарат элементтерінің өзара байланысын сезу үшін, мысалы, әртүрлі қиылыс схемасы, оларды сызып көрсету және белгілеу схемасы) және тақырып бойынша сызбалық жұмысты орындауға жол ашатын алгоритм бойынша үйрену тапсырма тобын орындауға бағыт береді. Осындай ойлау тіршілігінің тәсілін меңгеріп алу кез келген уақытта және кез келген түрде ойынан ғылыми ақпаратты саралап алуға жол береді, ғылыми білім негізінде кез келген графикалық сызықты талдауға мүмкіндік туғызады. «Инженерлік сызба» пәнге оқытудың түріне тәжірибелік сабақтар жатады. Нұсқаулықтың осындай үлгілерінде, бұйымдарды және иллюстрацияларды, репродуктивті барынша көп өздік жұмыстарды, сондай-ақ, шығармашылық деңгейді қолданады. Бұнда репродуктивті деп отырғанымыз, пәннің спецификалы сипаты сызықтар, оның көлемін оқытушы ұсынған үлгіде болуы дегенді аңғартады. «Инженерлік сызба» пәніне оқытудың тиімділігі және білім берілуі қанша ойластырылған болса да, оған білім берудің субъекті бола алатын студент бағытының қалыптасқанына байланысты және оған тәуелді.

«Инженерлік сызба» пәнін  шығарылған үлгіге және технологияға сәйкес тәжірибелік сабақтарында ұйымдастыру ерекшеліктерін мәліметтеп қарастыру негізгі нысанаға алынады.

Неғұрлым «Инженерлік сызба» пән курсы геометриялық және проекциялық сызбаның барлық негізгі стандарттарымен танысуды көздейтін болса, соғұрлым курстың басында дәрісте сол туралы теоретикалық қалпының негізі беріледі. Сондықтан бірінші тәжірибелік сабақтарында жылдық сызбаны көрсетумен Қазақстан Республикасының  мемлекеттік стандарт негізгі қаулысын қайталау жүргізіледі. Студенттермен орындалған үйрену тапсырмалары тексеріледі және студенттерге оқулықпен және анықтама әдебиеттерімен жұмыс жүргізу тәсілдері ұсынылады, осының барлығы графикалық жұмысты орындауға жол ашады. Тапсырманы орындауда қиындық туғызатын студенттерге дайын алгоритмді қолданып берілген тапсырманы Қазақстан Республикасының  мемлекеттік стандарт қаулысын пайдаланғанын қарап орындауға рұқсат етіледі Алгоритмді қолдануды ұсынғанда оларды орындаудың кезеңдері плакаттарда және нұсқауларда көрсетілумен мәліметті ауызша талдауы беріледі. Үлгі симметриялы бола алатын көз бөлінеді және оны орындауда белгілерді қолдануға тура келеді. Графикалық тапсырманы орындаудың осындай түрі жұмысты орындаудың технологиялық реттілігінің маңыздылығы студенттер мен тәжірибеде өңделеді және қандай дәрежеде орындағаны байқалады.

Білім берудің осы үдерісінде біз студенттерді белгілі толық шығармамен бірге шығармашылық әрекетшіліктің бөлік элементтерін меңгеруге және оны жүзеге асыруын қадағалаймыз:

- әрекетшіліктің белгілі тәсілдерін қиыстырғанда, белгісіз жағдайда әрекетшіліктің белгілі тәсілдерін пайдалану;

- субъект функциясының өзгеруінде, нысан құрамын анықтағанда, белгілі жағдайда мәселені көруін білу, шығармашылық әрекеттілікте алгоритм бойынша жұмыс істеу.

Шығармашылық білімді қалыптастыру үшін шығармашылық элементтерімен тапсырмалар беруі мүмкін:

- сызбалық орындау реттілігінің басқа нұсқауларын ұсыну;

- жұмысты орындаудың үйлесімді реттілігін анықтау;

- сызбалық жұмысты орындауға қандай белгілі тәсілдерін қиыстырғанда мүмкін болғанын анықтау;

- бөлік құралымына келесі өзгерістерді енгізу және т.б.

Шығармашылық жұмысты орындау барысында құрама одақты және логикалық ойлауды қоса оны қолданып құрастырылған үлгіні сызу, шығармашылық ойды дамытады.

Осындай жұмыста кейбір графикалық элементтерді орындау технологиясының біліміне басқа мақсаттар қосылады және автордың сызылатын нысанды өзінше көрсетіп ойын жеткізуге қызмет етеді.

Дәл осы сәтте оларды студент продуктивті деңгейде жақсы меңгерілген болса, шығармашылық тіршілікте талапты және жүзеге асыруға болатыны және сызбалық жұмыс тәсілдерінің меңгергені туралы гипотезасы тексеріледі. Осындай жұмысты орындау барысында оқытушының басқару рөлі өлшенбестей өседі. Осындай жұмысты орындағанда студенттер оқытушыдан және бір-бірінен кеңес сұрайды. Эскизді шығару және Қазақстан Республикасының мемлекеттік стандартының негізгі талаптарына оның сәйкестігін және жұмысты орындаудың ерекше технологиялық мүмкіндіктерін талқылау, оқытушының нұсқаулық жасауымен іске асады.Білім алушыларды қалдық білімдерін мамандығына пайдаланудың жіктелуін, біліммен тәрбиеленуі мамандыққа бейімдеу болып табылады. Сызбалық жұмысты орындағанда шығармашылық және репродуктивті тіршілік тәсілдерін игерудегі оқыту мақсаттарына жету сабақ нәтижесін сараптау тұрғысында және студенттердің графикалық тіршіліктің қолданған тәсілдерін есінде сақтап бекіту мақсатында өткізіледі. Сондықтан «Инженерлік сызба» пәніне оқыту тәжірибелік сабақтар сапасында жүзеге асады (орындалатын жұмыстың әрбір түрінің мақсатын нақты анықтау,  мақсаттарға сәйкес білім беру амалдарын, оқыту нысанын және құралдарын белгілі бір реттілікке қосып оқытудың инновациялық технологиясын сұрыптау, студенттерді оқыту, олардың ойын дамыту және логикасын ұштай алуына бағдарлау). Студенттерді оқытуда «Инженерлік сызба» пәні бойынша білімді қалыптастыруда бүгінгі жоғары оқу орнының студенттері – болашақта мамандардың жалпы мәдениетін қалпына келтіруі көзделеді. Кредиттік оқыту  жүйесіне  тиісті «Инженерлік  сызба» пәнінен оқулықтар бүгінгі жаңа технологияның  талап-мүддесін қанағаттандыра алмайды. Түйінді пікірімізді дәлелдеу мақсатында Ғ. Ақпанбековтың  «Сызба геометрия» оқулығынан үзінді келтіріп өту орынды [55]:

1 тарау. Проекциялау әдістері туралы жалпы түсінік.

1. Центрлік және параллель проекциялау.
2. Нүкте, түзу, жазықтық. Нүктенің эпюрі.
3. Берілген координаттары бойынша нүктенің эпюрін салу.
4. Түзулердің және олардың кесінділерінің проекциялары.
5. Түзудің іздері.
6. Түзу сызықтардың өзара орналасуы.
7. Жазықтықтар.

Көріп отырғанымыздай, жоғарыда оқулықтың құрылым-жүйесі кредиттік технология талаптарына сай келмейді.

Кредиттік технология талабына оқытушы-профессордың дәрісі  нұсқаулық сапасында 10 %-дан аспау үшін ақпараттық ғылыми негізде трансфармацияланып беріледі. Ал Ғ. Ақпанбековтың «Сызба геометрия» оқулығында ол мәлімет 10 %-дың шамасынан әлдеқайда артық. Сол себепті  аталған оқулықтың құрылым – жүйесін сақтай отырып, жаңа технологияның қағидасына сай үлгі жасауға мәжбүр болдық. Бұл іс-әрекетті орындау барысында типтік бағдарламасы ұсынылған  90 сағат шамасындағы іс- әрекетті жүзеге асыруға  ыңғайлы болу үшін оқулықты қайтадан жаңаша зерделедік.

«Модуль» деген ұғым бұл іс-әрекет барысында негізгі оқулықты бір үлгі мазмұнына салу тұрғысында қолданылды. Жоғарыдағы оқулықтағы 10 тарауды мен 10 модульге жіктеп, әрбір модульдік кіші  құрылымдарын блокқа саралап, осы нысандағы ұсынылған пән мазмұнындағы ғылыми негіздерді жеке сұрыптап, оларды студенттердің өздігінен дамытуы мақсатында мысалдар құрылып, оны орындаудың тапсырмалары  түзіліп, сұрақтар студенттердің аудиторияда меңгерген  10 % тірек ұғымының одан әрі ілгерілуіне зерттеу сапасында сұрыпталып және бұл іс-әрекетті стандарт шегінде студенттің дұрыс орындауына жеңілдік көрсету мақсатында әдебиеттер тізімі ұсынылды.

1 модуль инженерлік сызба пәні

1.1 блок Геометриялық формалар: орталық және параллель проекциялы сызбаларды алудың әдістері

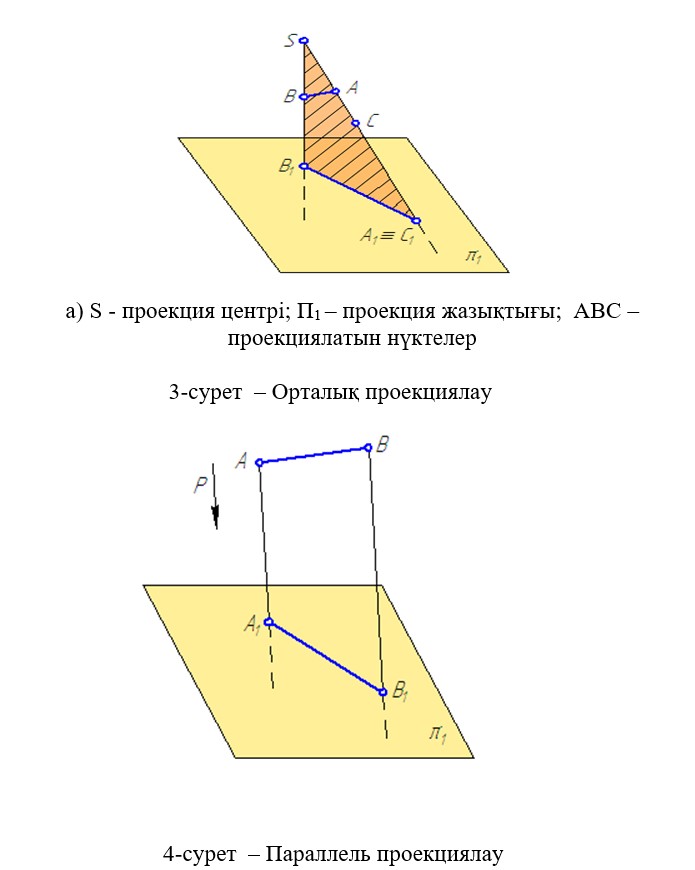
Фигураның белгілі бір ереже бойынша жазықтыққа түсірілген кескіні проекция деп аталады. Егер затта жазықтыққа кескіндеген кезде проекциялаушы сәулелер бір нүктеден тарайтын болса, онда мұндай әдісті орталық проекциялау деп атайды (3 сурет).

Орталық проекциялау әдісі сәулет және бейнелеу өнерінде кеңінен  қолданылады.

Орталық проекцияны кейде конустық немесе перспективалық проекция деп атайды. Егер нәрсе кескінін алуда өзара параллель проекциялаушы сәулелер қолданылса, онда мұндай әдісті  параллель проекциялау деп атайды. (4 сурет). Түзу мен жазықтықтың ортақ нүктесі олардың қиылысу нүктесі деп айтады.

Мысал

Тапсырма

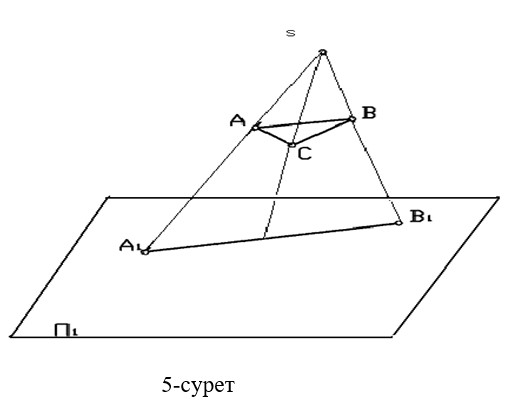
1.Кеңістікте орналасқан АВС нүктелерің орталықтан проекциялау əдісі арқылы салып көрсетіңіз  (5 сурет).

Сұрақтар

1. Сызбаны проекциялау əдістері дегеніміз не?
2. Орталықтан (центрлік) проекциялау əдісі дегеніміз не?
3. Параллель проекциялау əдісі дегеніміз не?

 

Әдебиеттер

1Есмуханов Ж. М. Сызба геометрия. – Алматы : Мектеп, 1987. –168 б.

2 Нəби Ы. А. Инженерлік графика. – Алматы, 2006.

3 Қонақбаев К. Қ. Сызба геометрия. – Алматы: 1971.

4 Есмұханов Ж. М. Сызба геометрия есептері. – Алматы: 1985.

 

1.2 блок Тік бұрыштап проекциялау әдісі

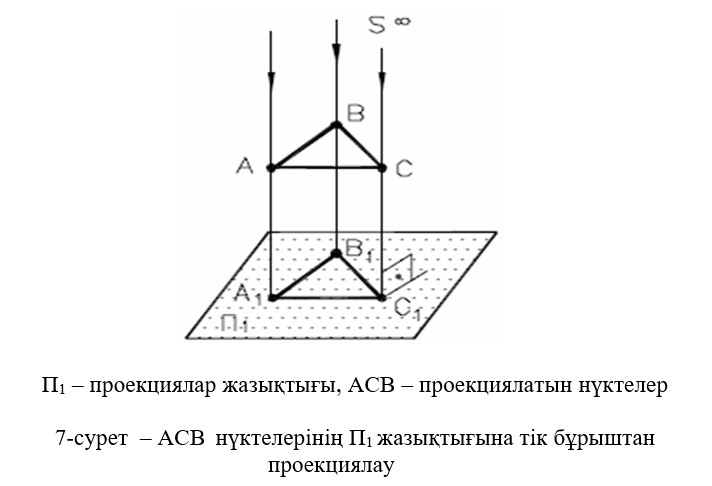
Проекциялау бағыты S проекциялар жазықтығына  перпендикуляр болатын параллель проекциялардың жеке түрін тік бүрыштап проекциялау дейді. Берілген АВ түзуінің П жазықтығындағы кескінін салу үшін, одан П₁ жазықтығына перпендикуляр түсірейік. Жазықтыққа перпендикуляр  деп сол жазықтықпен 90¢ бұрыш жасайтын түзуді айтады.

АСВ түзулерінен  П  жазықтығына түсірілген перпендикулярдың табаны А₁С₁В₁ нүктелерден П₁ жазықтығындағы тік бұрыш проекциясы  (7сурет).

Мысал:

Тапсырма

1. Берілген АВ кесіндісін П₁ жазықтығына тік бұрыштап проекциялау керек (8-сурет).

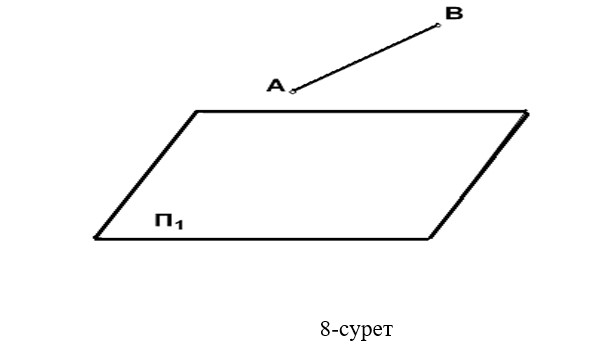
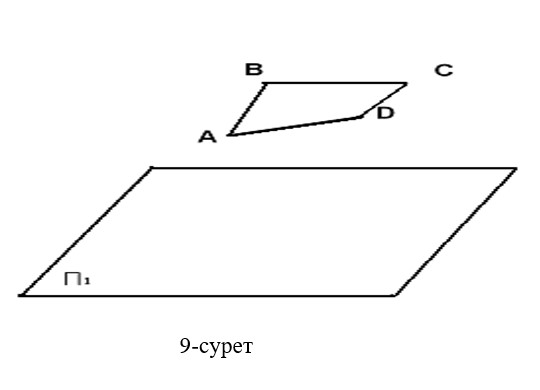
2. АВСD төртбұрышты тік бұрыштап П₁ жазықтығына проекциялау керек (9-сурет).

Сұрақтар

1. Тікбұрышты параллель проекциялау əдісі дегеніміз не?
2. Жазықтықта нәрсе кескіні қалай салынады?
3. 3. Жазықтыққа перпендикуляр деп нені айтады?

 

 

Әдебиеттер

1 Ақпанбек Ғ. Сызба геометрия. – Алматы.: Ы.Алтынсарин атындағы Қазақ Білім академиясының Республикалық баспа кабинеті, 1998. – 208 б.

2 Есмуханов Ж. М., Қонақбаев Қ. Қ. Сызба геометрия. – Алматы: Мектеп, 1968. – 217 б.

3 Ыбраев А. Инженерлік графика. – Алматы: 2006.

4 Қонақбаев К. Қ. Сызба геометрия. – Алматы: 1971.

5 Есмұханов Ж. М. Сызба геометрия есептері. – Алматы: 1985.

 

1.3 блок. Қиғаш бұрыштан проекциялау

Егер өзара параллель  проекциялаулы сәулелер проекция жазықтығына 90 °С -қа тең емес кез келген бұрыш жасай түсетін болса, онда мұндай әдіс қиғаш бұрыштан проекциялау деп аталады (10-сурет).

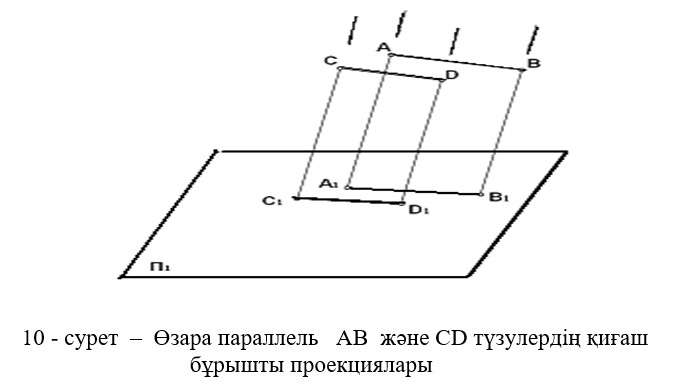
Кеңістіктегі фигуралардың параллель проекцияларындағы өзгерссіз сақталатын қасиеттерін инварианттар деп атайды.

Проекциясы бойынша кеңістіктегі нәрсенің  пішінін ойша анықтау мүмкін болмаса, мұндай кескіндерді қайтымсыз дейді. Нәрсенің пішіні, өлшемдері, ерекшеліктері туралы мағлұматтар сызба арқылы танылатын  болса, сызба қайтымды болады.

Тапсырма

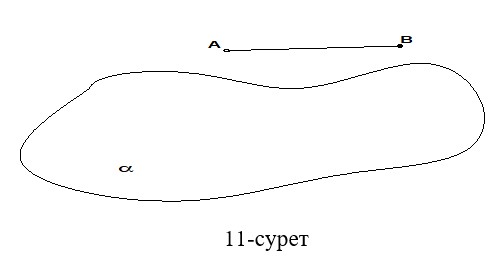
  1.АВ  түзуін α жазықтығына қиғаш бұрышты проекциясын cалыңыздар (11-сурет).

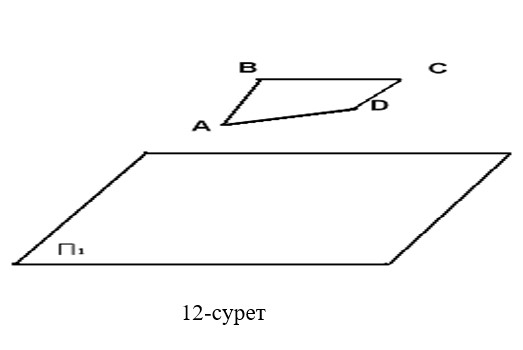
2.АВСD төртбұрышты қиғаш бұрыштап П₁ жазықтығына проекциялау керек (12-сурет).

Сұрақтар

1. Қиғашбұрышты параллель проекциялау əдісі дегеніміз не?
2. Жазықтықта нәрсе кескіні қалай салынады?
3. Қандай сызбаларды қайтымды немесе қайтымсыз дейді?
4. Инварианттар деп нені айтады ?

5.Кескінделуші сəулелер дегеніміз не?

 

Әдебиеттер

1 Есмуханов Ж. М. Сызба геометрия. – Алматы: Мектеп, 1987. –168 б.

2 Ақпанбеков Ғ. Ә. Сызба геометрия. - Алматы: Қазақ университеті, 1992. -  120 б.

3 Бəйдібеков Ə. К. Сызба геометрия (сандық белгілері бар проекцияларда). -Тараз: 1999.

4 Ыбраев А. Инженерлік графика. – Алматы, 2006.

5 Қонақбаев К. Қ. Сызба геометрия. – Алматы, 1971.

6 Есмұханов Ж. М. Сызба геометрия есептері. – Алматы, 1985.

 

2 модуль      Геометриялық элементтердің (нүктелер, түзулер және жазықтықтар) кешенді сызбалар

 

2.1  блок Нүктенің проекциясы

Бұл пəнде нүктенің анықтамасы мен түсініктемесі жоқ. Сондықтан нүктенің алу жолын мысалмен көрсетейік.

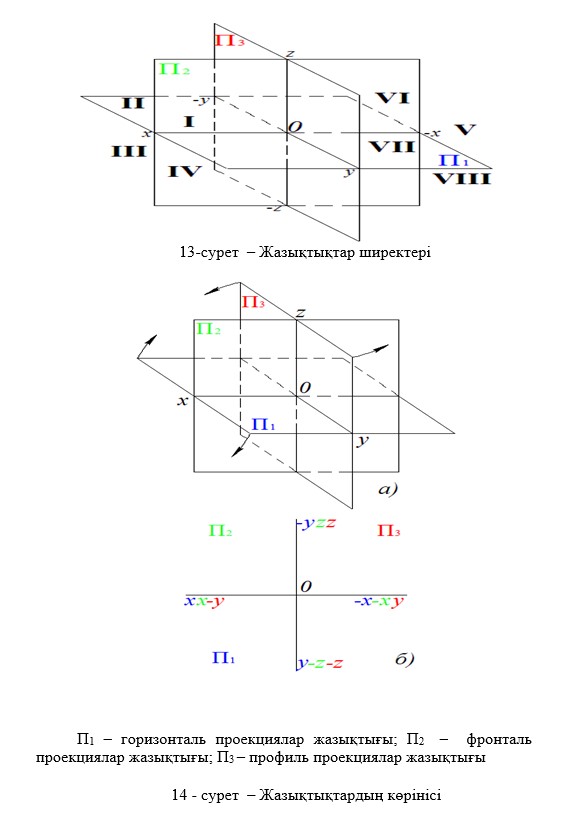
Өзара перпендикуляр екі жазықтық кеңістікті  ширектер деп аталатын төрт бөлікке бөледі (13-сурет).

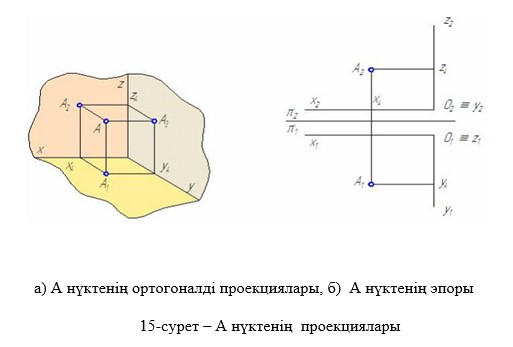
Берілген нүктенің сызбасын алу үшін оны осы П_1, П₂ және П₃ жазықтықтарына  тікбұрыштап проекциялаймыз. Сонда нүктенің П₁ жазықтығындағы тікбұрышты проекциясын оның горизонталь проекциясы, П₂ жазықтығындағы тікбұрышты проекциясын оның фронталь проекциясы және П₃ жазықтығындағы тікбұрышты проекциясын оның профиль проекциясы  деп атайды. П₁ жазықтығын горизонталь проекциялар жазықтығы, П₂ жазықтығын фронталь проекциялар жазықтығы және П₃ жазықтығын профиль проекциялар жазықтығы деп   айтады. Кеңістікте П₁, П₂ және П₃ жазықтықтары сегіз бөлікке бөлінеді. Осы бөліктерді октанттар деп атайды. Жазықтықтарды сызба жазықтығымен беттестіргенде шығатын кескінді эпюр деп айтады  (14-сурет, а.б) Кейде эпюр деудің орнына кешенді сызба, немесе сызба деп айтады. Сызуда фронталь проекцияны алдынан қарағандағы көрініс, горизонталь проекцияны үстінен қарағандағы және профиль проекцияны сол жағынан қарағандағы көріністер деп атайды. Алдынан, үстінен және сол жағынан қарағандағы көріністер негізгі көріністерге жатады. Осыған орай эпюрді  негізгі көріністер сызбасы деп те атайды.Нүктенің фронталь және горизонталь проекцияларын қосатын түзу  х өсіне перпендикуляр болады, яғни вертикаль орналасады. Сондықтан оны вертикаль байланыс сызығы дейді. Ал фронталь және профиль проекцияларын қосатын түзу z өсіне перпендикуляр болады, яғни горизональ орналасады. Сондықтан оны фронталь байланыс сызығы деп атайды. (А₂ А₁) – вертикаль байланыс сызығы; (А₂ А₃) – горизонталь байланыс сызығы. Нүктенің фронталь және горизонталь проекцияларының ара қашықтығы оның ординатасы мен аппликатасының қосындысына тең. Ал фронталь және профиль проекцияларының ара қашықтығы абциссасы мен ординатасының қосындысына тең болады (15-сурет)

А₂ А₁ = y+z; |А₂ А₃| = x+y

 

Бір нүктенің проекцияларын жалғастыратың түзулерді проекциялық байланыс сызықтары деп атайды.

Мысал

Тапсырма

1. А (35;25;15) нүктенің эпюрасы мен сандық белгілері бар проекциясын салып көрсетіңіз.
2. C (20;25;-50) нүктенің эпюрасын салып көрсетіңіз
3.  А(15;25;40) жəне В(20;-10; 15) нүктелері қай ширектерде орналасқанын анықтаңыз.

     

                                           

Сұрақтар

1. Монж эпюрі дегеніміз не?
2. Нүктелердің фронталь проекциясы дегеніміз не?
3. Октанттар деген не ?
4. Октанттар қайдан шығады ?
5. Эпюрді оқу деп нені айтады ?

 

Әдебиеттер:

1 Есмуханов Ж.М. Сызба геометрия есептері. - Алматы: Білім, 1995.

2 Сызба геометрия. Қонақбаев К. Астана, «Фолиант» баспасы, 2011.-176 бет

3 Сызба геометрия және инженерлік графика. Нәби Ы. – Алматы «Мектеп» баспасы, 2005.-264 б.

4 Ыбраев А. Инженерлік графика. – Алматы, 2006.

5 Қонақбаев К. Қ. Сызба геометрия. – Алматы,1971.

6 Есмұханов Ж. М. Сызба геометрия есептері. – Алматы, 1985.

 

2.2 блок. Түзу сызықтың проекциясы

Түзу сызық дегеніміз - бір түзу бойындағы нүктелер жиынтығы.

Түзудің проекцияларын алу үшін, оның кез келген екі нүктесінің аттас проекцияларын түзулермен қосады. Түзудің проекциясы – түзу болады. Екі нүктеден өткен түзуді кесінді дейміз.

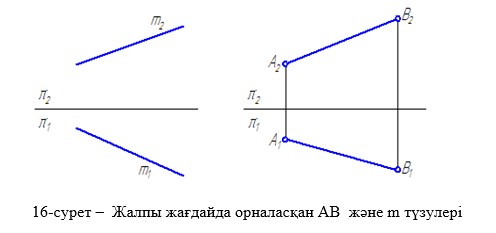
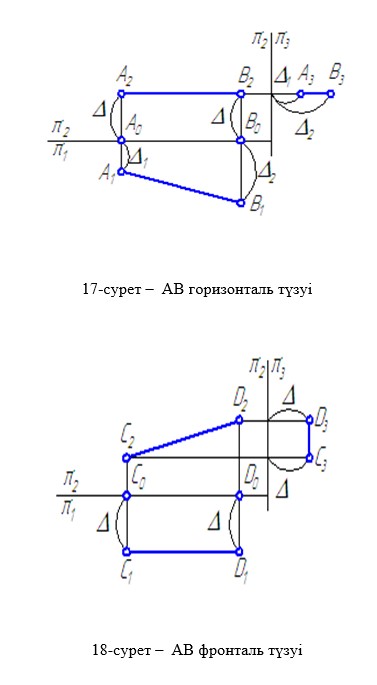
Проекция  жазықтықтарының ешқайсына параллель емес түзулер жалпы жағдайдағы түзулер деп аталады (16-сурет). Бір  проекция жазықтығына параллель болатын түзулер денгейлік түзулер деп аталады. Горизонталь проекция жазықтығына параллель түзулер горизонталь деп аталады және оны h әріпімен белгілейді ( 17-сурет). Фронталь проекция жазықтығына параллель түзулер фронталь деп аталады және оны f  әріпімен белгілейді (18-сурет). Профиль проекция жазықтығына параллель түзулер профиль деп аталады және оны p әріпімен белгілейді ( 19-сурет).

Кеңістікте түзу проекция жазықтығына перпендикуляр орналасса, онда проекциялаушы түзу деп аталады.

Горизонталь проекциялаушы түзу деп горизонталь проекция жазықтығына перпендикуляр түзулерді айтады ( 20-сурет). 

Профиль проекциялаушы түзу деп профиль проекция жазықтығына  перпендикуляр түзулерді айтады ( 22-сурет).

Фронталь проекциялаушы түзу деп фронталь проекция жазықтығына перпендикуляр түзулерді айтады ( 21-сурет).

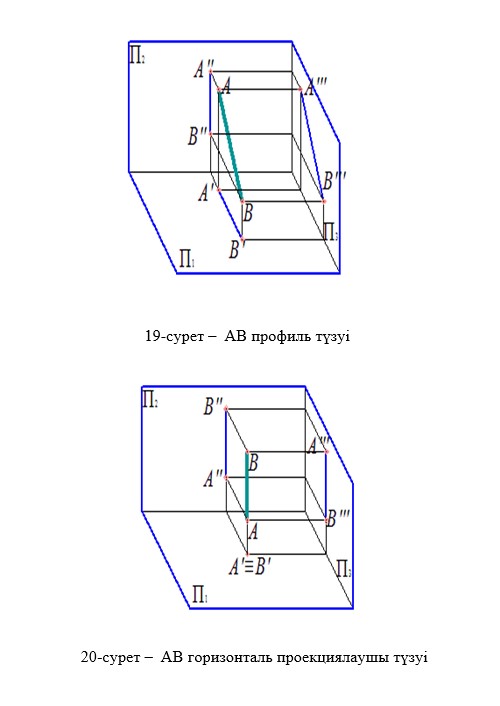
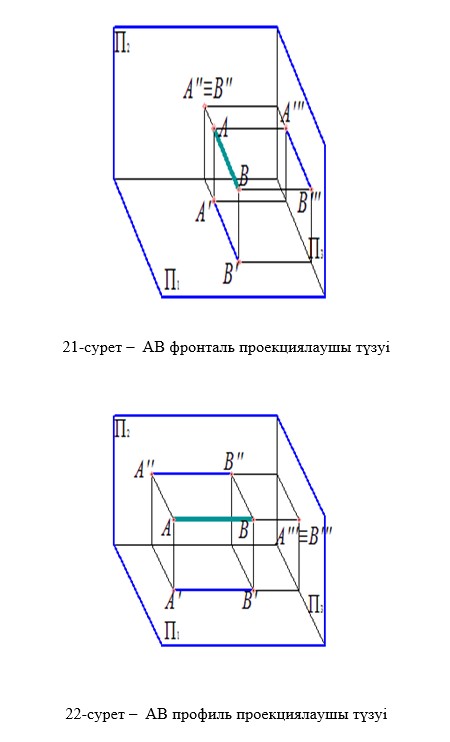
Тапсырма

1. АВ түзуінің жетіспейтін проекциясын салу қажет 23 сурет.

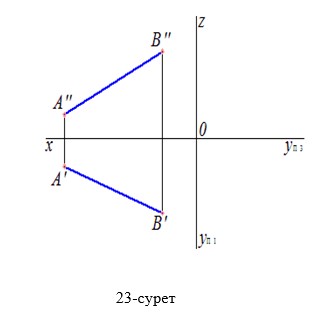
2) А (15; 30; 45) жəне В (40; -10; 15) нүктелерінің проекцияларын профиль проекция жазықтығында салып көрсетіңіз.

3) А (45; 30; 15) жəне В (100; -10; 25) нүктелерінің проекцияларын профиль проекция жазықтығында салып көрсетіңіз.

 

Сұрақтар

1. Деңгейлік түзу сызықтар дегеніміз не?
2. Параллель түзу сызықтар дегеніміз не?
3. Проекциялаушы түзулер деген не?
4. Жалпы жағдайдағы түзулер деп қандай түзулер аталады?

 

Әдебиеттер

1 Ақпанбеков Ғ. Сызба геометрия. – Алматы : Ы. Алтынсарин атындағы Қазақ Білім академиясының Республикалық баспа кабинеті, 1998. –  208 б.

2 Ақпанбеков Ғ. Ә. Сызба геометрия. – Алматы : Қазақ университеті, 1992. – 120 б.

3 Ыбраев А. Инженерлік графика. – Алматы, 2006.

4 Қонақбаев К. Қ. Сызба геометрия. – Алматы, 1971.

        5 Есмұханов Ж. М. Сызба геометрия есептері. – Алматы, 1985.

Түзу сызықтың ізі

Түзудің іздері деп оның проекциялар жазақтарымен қиылысу нүктелерін айтады. Бізде үш проекция жазықтықтары болғандықтын, түзу сызықтың үш ізі болады.

Олар өздері жататын проекция жазықтықтарының атымен аталады (24 сурет). М – түзудің горизонталь ізі. N –түзудің фронталь ізі. М₁ – горизонталь іздің горизонталь проекциясы. М₂ – фронталь іздің фронталь проекциясы. N₁ – фронталь іздің фронталь проекциясы. N₂ – фронталь іздің горизонталь проекциясы.

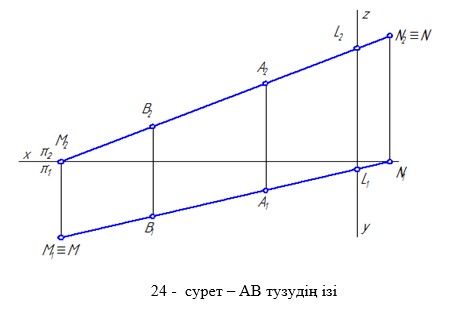
Түзу мен оның проекциясының арасындағы бұрышты,түзудің проекция жазықтығына көлбеу бұрышы деп атайды. Байланыс сызықтарының түзудің горизонталь проекциясымен қиылысуы горизонталь ізді, байланыс сызықтарының түзудің фронталь проекциясымен қиылысуы фронталь ізді және профиль проекциясымен қиылысуы профиль ізді береді.

AB сызықтың ізің салу үшін мыналар қажет:

А₂В₂ түзумен П₂ проекция жазықтығындағы проекциясын А нүктесінен В нүктесіне қарай х өсіне дейін созып, М₂ нүктесін белгілейміз. Содан кейін П₁ проекция жазықтығындағы А₁ В₁ түзу сызығының проекциясын в нүктесінен А нүктесіне қарай  Х өсіне дейін созып, N₁ нүктесін анықтап, сәулесін жүргіземіз. М₂ және N₁ нүктелерінен жүргізілген сәулелер А1 В1 және А₂В₂ проекцияларының созындысымен М₁ және N₂ нүктелерінде қиылысады.Бұл табылған нүктелер кеңістікте орналасқан жалпы жағдайдағы Ав түзудің П₁ және П₂ проекция жазықтығындағы горизонталь және фронталь іздері болады.

 

Тапсырма

1.Жалпы жағдайда орналасқан А (20; 30; 30) және С (35; 25; 50) төбелерінен тұратын тузудің П₁ және П₂ проекция жазықтығындағы ізін салыңыз.

2.Жалпы жағдайда орналасқан А(40; 50; 50) және В(55; 45; 70) төбелерінен тұратын тузудің П₁ және П₂ проекция жазықтығындағы ізін салыңыз.

3. СВ тузудің ізін салыңыз (25 сурет)

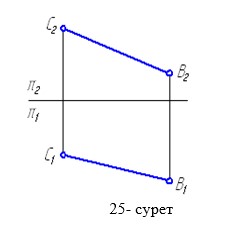
4.Түзулердің өзара қалай орналасқандарын табе қажет, АВ және CD түзулерінің EF түзуімен қиылысуын табе керек

Сұрақтар

1. Түзудің ізі дегеніміз не?
2. Іздер деген тақырыпта М - дегеніміз не?
3. Іздер деген тақырыпта N - дегеніміз не?
4. Іздер деген тақырыпта М1 - дегеніміз не?
5. Іздер деген тақырыпта М2 - дегеніміз не?
6. Іздер деген тақырыпта N1 - дегеніміз не?
7. Іздер деген тақырыпта N2 - дегеніміз не?

 

Әдебиеттер

1 Ақпанбеков Ғ. Сызба геометрия. – Алматы : Ы. Алтынсарин атындағы Қазақ Білім академиясының Республикалық баспа кабинеті, 1998. –  208 б.

2Ақпанбеков Ғ. Ә. Сызба геометрия. – Алматы : Қазақ университеті, 1992. – 120 б.

3 Ыбраев А. Инженерлік графика. – Алматы, 2006.

4 Қонақбаев К. Қ. Сызба геометрия. – Алматы,1971.

5 Есмұханов Ж. М. Сызба геометрия есептері. – Алматы, 1985.

 

2.4   блок     Жазықтықтың проекциясы

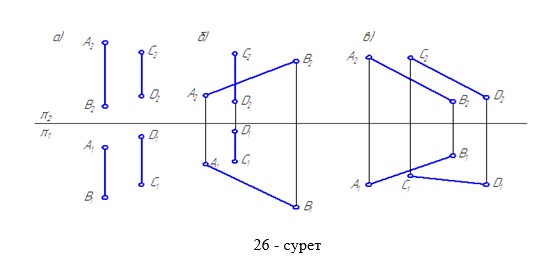
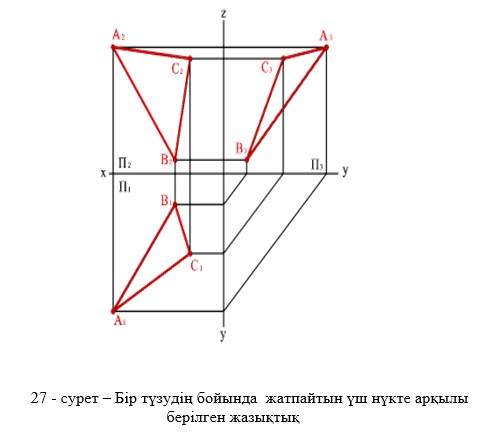
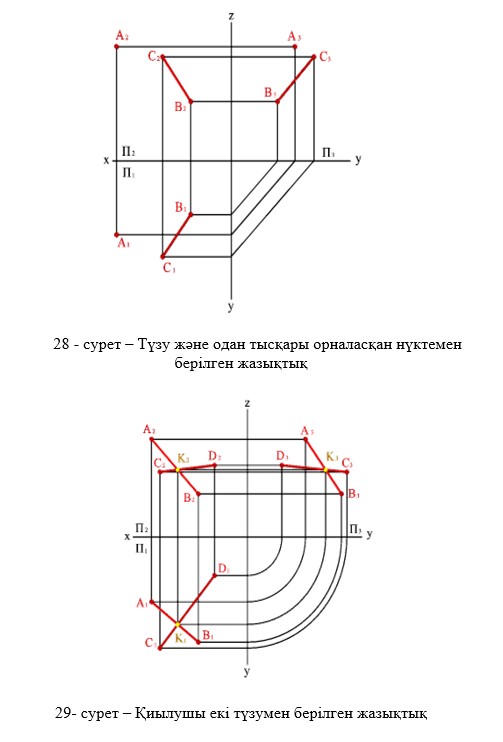
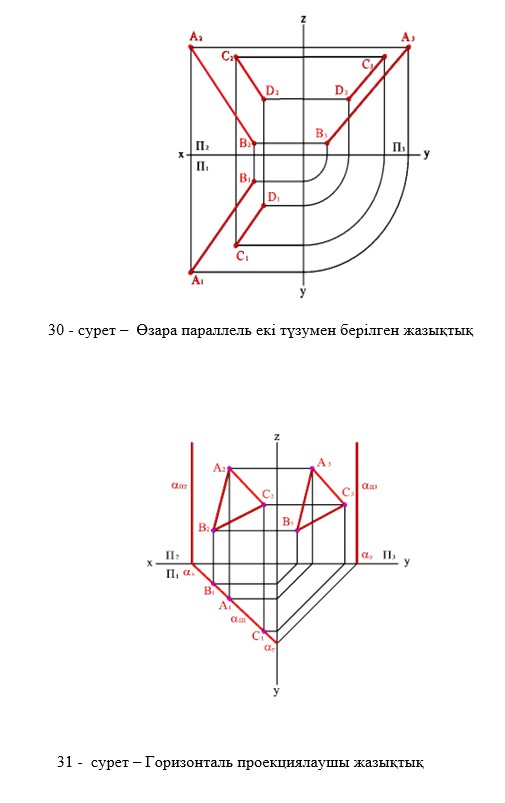
Кеңістікте жазықтықтар шексіз деп есептеледі. Жазықтықтар кеңістікте орналасуына қарай жалпы  келесі түрде  беріледі:                    а) бір түзудің бойында  жатпайтын үш нүкте арқылы (27-сурет),             б) түзу және одан тысқара  орналасқан нүкте  арқылы (28-сурет),                 в) қиылушы екі түзумен (29-сурет), г) өзара параллель екі түзумен            (30-сурет )  

Проекция жазықтықтарын параллель немесе перпендикуляр болатын жазықтықтарды дербес жағдайдағы жазықтықтар деп  атайды.

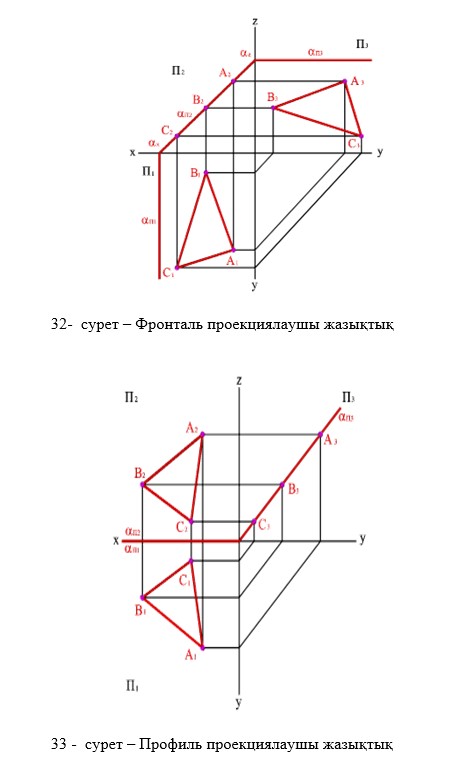
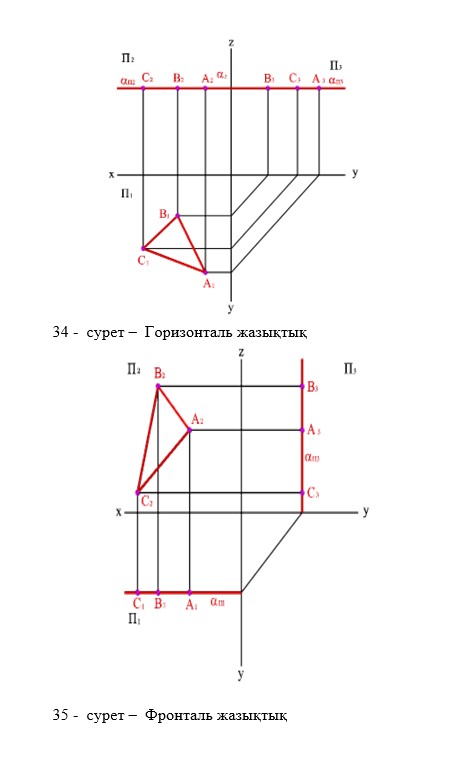
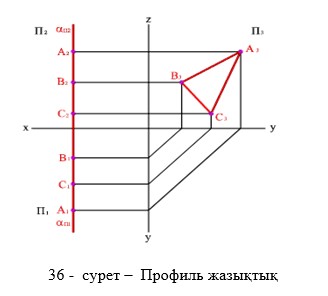
Егер берілген  жазықтық горизонталь проекция жазықтығына перпендикуляр  болса, онда  мұндай жазықтықты горизонталь проекциялаушы жазықтық деп атайды (30-сурет). Егер берілген  жазықтық фронталь проекция жазықтығына перпендикуляр  болса, онда  мұндай жазықтықты фронталь проекциялаушы жазықтық деп атайды (31-сурет). Егер берілген жазықтық профиль проекция жазықтығына перпендикуляр  болса, онда мұндай жазықтықты профиль проекциялаушы жазықтық деп атайды (32-сурет).

Проекция өсі бойымен өтетін жазықтықтырды өстік проекциялаушы жазықтықтар деп атайды. Егер өстік проекциялаушы жазықтықтардың проекция жазықтықтарына көлбеу бұрыштары өзара тең болса, онда биссектор жазықтығы деп аталады.

Денгейлік жазықтықтар проекция жазықтықтарының біреуіне параллель орналасады, ал қалған екі проекция жазықтығына перпендикуляр. Горизонталь проекция жазықтығына параллель жазықтықты горизонталь жазықтық деп атайды (33-сурет).

 Фронталь проекция жазықтығына параллель жазықтықты фронталь жазықтық деп атайды (34-сурет).

 Профиль проекция жазықтығына параллель жазықтықты профиль жазықтық деп атайды (35-сурет).

 

Мысал

Тапсырма

1. Берілген АВС және ЕDF жазықтықтарының эпюрын тұрғызыныз. А (50; 45; 45), В (55; 60; 85), С (25; 30; 45) және                 Е (50; 5; 35), D (55; 50; 85),  F (57; 65; 45).
2. Дербес жағдайда орналасқан горизонталь проекция жазықтығына параллель А, В жəне С төбелерінен тұратын жазықтықтың проекциясын салып көрсетіңіз.
3. А (15; 25; 45); В (35; 45; 45) жəне С(25; 15; 20) төбелерінен тұратын жазықтықтың П₂ жəне  П₁  проекция жазықтығындағы ізін салып көрсетіңіз.
4. Берілген АВС жазықтығының профиль проекциясын салыңыз (37 сурет).

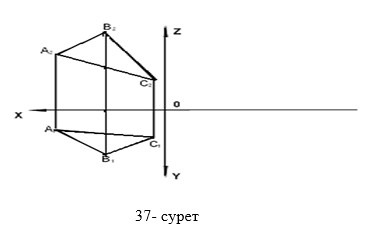
Сұрақтар

1. Жазықтықтар кеңістікте орналасуына қарай жалпы қандай түрде беріледі?
2. Қандай жазықтықтар денгейлік жазықтықтар деп аталады?
3. Дербес жағдайдағы деп қандай жазықтықты айтады?
4. Қандай жазықтықтар жалпы жағдайдағы жазықтықтар деп аталады?

 

Әдебиеттер

1 Есмуханов Ж. М., Қонақбаев Қ. Қ. Сызба геометрия. – Алматы : Мектеп, 1968 .

2 Қонақбаев Қ. Қ. Сызба геометрия. – Алматы: Мектеп, 1971. – 164 б.

3 Нәби Ы. А. Сызба геометрия негіздері. – Алматы, 1994. – 162 б.

4 Ыбраев А. Инженерлік графика. – Алматы, 2006.

 

3 модуль Позициялық және метрикалық есептер

Позициялық (тұрғылықты) және метрикалық (өлшем) есептер жалпы инженерлік сызбаның негізгі есептері болып табылады.

Позициялық (тұрғылықты) есептер дегеніміз – геометриялық фигуралардың сызбалары арқылы олардың кеңістіктегі өзара орналасуын анықтайтың есептер.

Позициялық есептерге: нүкте мен түзудің, түзу мен түзудің, нүкте мен жазықтықтың, түзу мен жазықтықтың, жазықтық пен жазықтықтың, жазықтық пен беттің, екі беттің өз-ара орналасу есептері жатады.

Метрикалық есептер дегеніміз- геометриялық фигуралардың сызбалары арқылы лоардың кеңістіктегі өзара қашықтықтарын, олардың арасындағы бұрышын және олардың ауданың, нақты шамасын жағдайын анықтайтын есептер.

 

3.1 блок. Позициялық есептер

3.1.1 Нүкте мен түзудің өзара орналасуы

Кеңістікте нүкте мен түзу әртүрлі жағдайда кездесуі мүмкін.Кеңістікте нүкте түзу бойында немесе түзуден тыс орналасуы мүмкін.

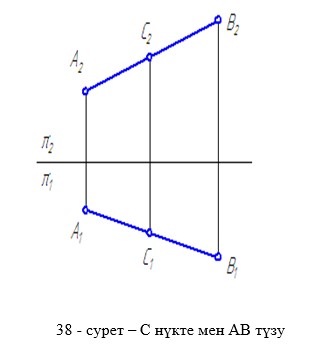
38 суретте нүктемен түзудің өзара орналастыруын осы тақарыпқа мысал қарастырамыз. Суретте С нүкте мен АВ түзудің горизонталь және фронталь проекция жазықтығындағы түзу сызығының горизонталь жəне фронталь проекция жазықтығындағы эпюрасы берілген.

Кеңістікте орналасқан С нүктесі АВ түзудің  горизонталь және фронталь проекция жазықтықтарындағы кескіндерінің бойында жатқан нүкте, яғни С нүктесі АВ түзуіне тиісті немесе түзу бойында орналасқан нүкте.

3.1.2 Түзулердің өзара орналасуы

Түзулер кеңістікте өзара орналасуына байланысты: параллель, қиылысқан, айқасқан және перпендикуляр болып келеді.

Егер кеңістіктегі екі түзу көлденең проекция жазықтығына кескіндерінің кескін табандары өзара параллель, ен аралықтары тең және сандық белгілері бір бағытта өсетін болса, онда мұндай түзулерді өзара параллель түзулер дейді (39 сурет).

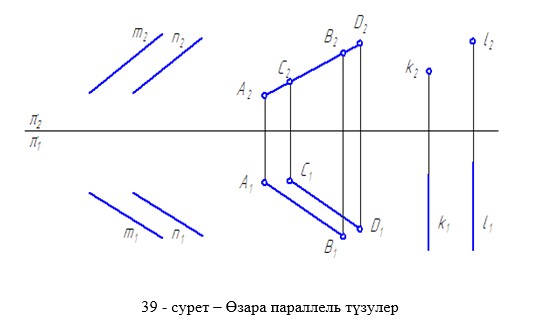
Егер, екі түзудің табандары бір нүктеде қиылысса және осы нүктедегі сандық белгілері бірдей болса, ондай түзулер өзара қиылысқан түзулер деп аталады (40 сурет).

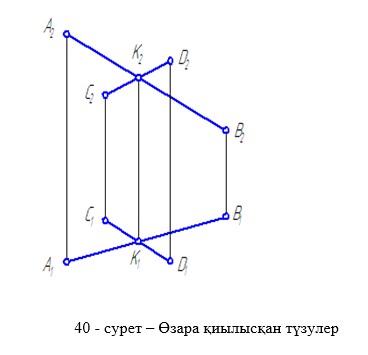
Егер кеңістіктегі екі түзу кескін табандары қиылысқан болса, бірақ ортақ қиылысу нүктесі болмаса және түзулердің ен аралықтары әртүрлі болса, онда мұндай түзулер өзара айқас түзулер деп аталады (41 сурет).

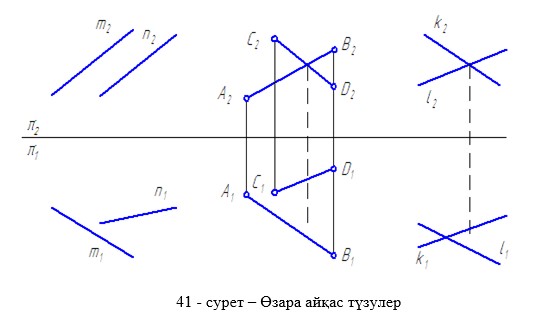
3.1.3 Екі жазықтықтардың өзара орналасуы

Кеңістікте екі жазықтық қиылысады, немесе параллель болады. Екі жазықтық өзара параллель болуы үшін олардың біреуіне қиылысатын екі түзуі екіншісінің сәйкес екі түзуіне параллель болулары қажет (42 сурет).

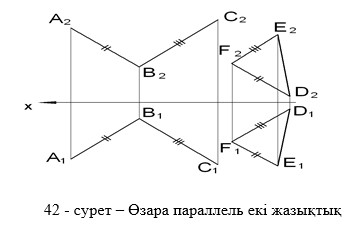
Егер әр түрлі екі жазықтық ортақ нүктесі болса, олардың қиылысуы түзу болады. Мұндай жазықтықтар қиылысушы жазықтықтар деп аталады. Екі жазықтық түзу сызық бойымен қиылысатын болғандықтан, қиылысу сызығын салу үшін олардың екі ортақ нүктесін тапса болды (43-сурет).

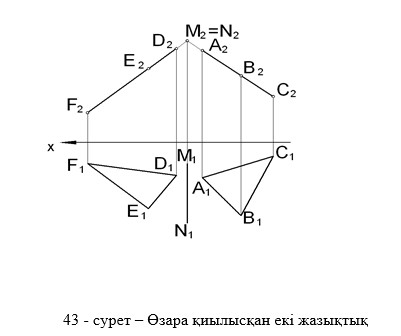
3.1.4 Түзу мен жазықтықтың өзара орналысуы

Түзу мен жазықтық кеңістікте өзара  параллель, қиылысатын және перпендикуляр болып кездеседі.

Кеңістікте орналасқан жазықтыққа меншікті екінші бір кеңістікте орналасқан түзу параллель болса,  онда бұл түзу жазықтыққа параллель түзу болады (44-сурет).

45 суретте кеңістікте орналасқан АВС жазықтығы мен осы жазықтық бойынша орналасқан DK түзуінің П₁ горизонталь және П₂ фронталь проекция жазықтықтарындағы проекциялары берілген. Егер жазықтыққа меншікті DK түзуінің горизонталь және фронталь проекция жазықтығындағы проекциялары D₁ K ₁ және D₂ K₂  түзудің проекцияларына параллель орналасса,  онда бұл түзу жазықтыққа параллель түзу болады.

Егер түзу жазықтыққа меншіксіз немесе жазықтыққа параллель  болмаса, онда мұндай түзу жазықтықпен қиылысатын түзулер болып, бір ғана қиылысу нүктесі болады (45-сурет).

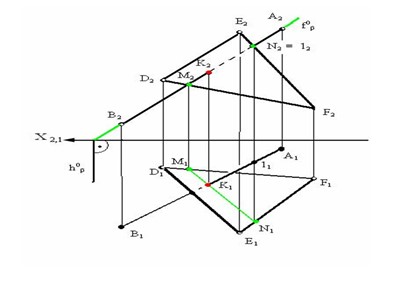
45 суретте кеңістіктегі жалпы жағдайда орналасқан ЕFD жазықтығы мен осы жазықтықпен қиылысатын АВ түзудің П₁ горизонталь және П₂ фронталь  проекция жазықтықтарындағы проекциялары берілген. Кеңістіктегі жазықтықпен түзудің қиылысу нүктесін табу үшін АВ түзудің проекция жазықтығындағы проекциясы арқылы  f фронталь проециялаушы жазықтығын жүргіземіз. Бұл f жазықтығын жүргізіп отырған себебіміз – екі жазықтықтың қиылысу сызығын анықтау. Осы қиылысу сызығын табу үшін, f фронталь проекциялаушы жазықтығын  ЕFD  жазықтығының фронталь  проекциясының  Е₂F₂ және F₂ D₂ қырларымен  қиылысу нүктелерін анықтаймыз. Байланыс сызығының көмегімен табылған қиылысу нүктелерінін горизонталь проекцияларын табамыз. Бұл табылған нүктелерін өзара қосып, екі жазықтықтың қиылысу сызығын анықтаймыз. Бұл жерде К нүктесі түзу мен жазықтықтың қиылысу нүктесі болады.

 

Сұрақтар

1.Позициялық есептер дегеніміз не?

2. Нүкте мен түзу сызықтар өзара қалай орналасады?

3.Түзу сызықтар өзара қалай орналасады?

4.Жазықтықтар өзара қалай орналасады?

5.Жазықтық пен түзу сызық өзара қалай орналасады ?

6.Метрикалық  есептер дегеніміз не?

 

Тапсырмалар

1. Кеңістікте орналасқан А (30; 30; 30); В (35; 25; 40) және E (35; 35; 20); F (20; 30; 35) төбелерінен тұратын түзулердің өзара орналасуларын салып көрсетіңіз.
2. Кеңістікте орналасқан өзара параллель түзулерді салып көрсетіңіз.
3. Жалпы жағдайда орналасқан кеңістіктегі А (30; 30; 30); В (35; 25; 40) және E (35; 35; 20) төбелерінен тұратын жазықтық пен                С (15; 15; 10); F (20; 30; 35) төбелерінен тұратын түзу сызықтың өзара орналасуларын салып көрсетіңіз.

4.Кеңістікте орналасқан А (30; 30; 30); В (35; 25; 40) және                        E (35; 35; 20) жазықтығының бойында жатқан F  (10; 15; 25) нүктесінен перпендикуляр түзу сызығын салып көрсетіңіз

5. К нүктенің фронталь проекциясын тұрғызу қажет (46 сурет)

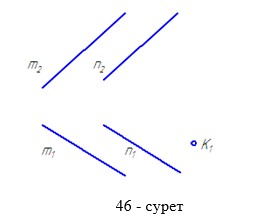
Әдебиеттер

1 Есмуханов Ж. М., Қонақбаев Қ. Қ. Сызба геометрия. –  Алматы : Мектеп, 1968 .

2 Қонақбаев Қ. Қ. Сызба геометрия. – Алматы: Мектеп, 1971. – 164 б.

3 Нәби Ы. А. Сызба геометрия негіздері. – Алматы, 1994. –  162 б.

4 Ыбраев А. Инженерлік графика. – Алматы, 2006.

5 Қонақбаев К. Қ. Сызба геометрия. – Алматы, 1971.

6 Есмұханов Ж. М. Сызба геометрия есептері. – Алматы, 1985.

 

Қорыта келгенде, «Инженерлік сызба» пәнінің негізгі оқулығын  бір үлгі деп алсақ, оның бұрынғыша тарауларын мәнділік сапада өзара іліктестік, сәйкестілік қағидада жүгіндіріп, модульдарға жіктедік. Бір модульден бірнеше (стандарт талабына сай) блоктарды түздік.

Сөйтіп, алдымен оқытушы-профессорлар студенттерге ұсынатын нұсқаулық дәрістерді трансформацияладық. Осы нұсқаулықты студенттердің өздігінен кеңейтуі үшін мысалдар мәтінін бердік. Содан кейін силлабусқа сай келерлік тапсырмалар мен сұрақтарды ұсындық. Сұрақтар деңгейліктерге қарай құбылып отыратынын ескердік. Әрбір модульден кейін рейтингі талабы мен мониторинг қорытындысы шығып отырады.