2.1 Электростатикалық өрістің дифференциалды түрдегі негізгі теңдеулері

 

Электростатикалық деп байқаушыға уақытылы өзгертілмеген , тіркелген зарядтардың өрісін айтады. Қарастырылып жатқан ортада магниттелген телімдер жоқ болса және де электр заряды пайда болса, онда теңдеулер жүйесіне (1.8) үш теңдеу жатады: 

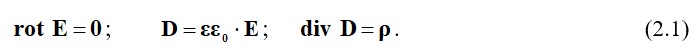
Бірінші теңдеу (2.1) көрсеткендей, электростатикалық өріс потенциал болып табылады, бұл мүмкіндік. Кез келген тұйық контур үшін СТОКС теоремасы арқылы аламыз

Электростатикалық өрісінде жабық контур бойынша E векторының сызықты интегралы нөлге тең болады. Бұл екі нүкте арасындағы кернеудің төмендеуі () Электростатикалық өріс интеграция жолын таңдаумен емес, сонымен бірге осы нүктелердің орналасуымен анықталады.

Бұл жағдай электростатикалық потенциалдың тұжырымдамасын енгізуге мүмкіндік берді.

Электростатикалық өрістің әлеуеті кез-келген нүктеде электростатикалық өрістің күшін бір нүктеден өріс нүктесіне дейін бір позитивті зарядты ауыстыру бойынша орындалатын жұмыс ретінде анықталады, онда потенциал нөлге тең болады 

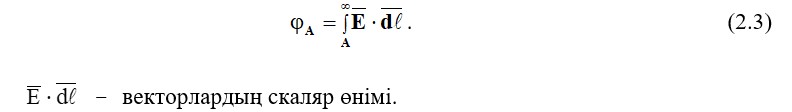
Мысалмен түсіндірейік. А нүктесінің потенциалын анықтаймыз (2.1-сурет), оның орналасқан жері шығуына қатысты белгілі

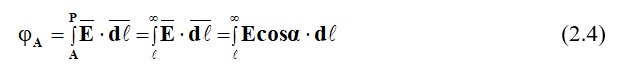
dℓ - векторы, ұзындық элементі, ауыстыру жолына қатысты. Формуланың екі жағын (2.4) dℓ (төменгі шегі) бойынша дифференциациялау кезінде біз төмендегілерді аламыз:

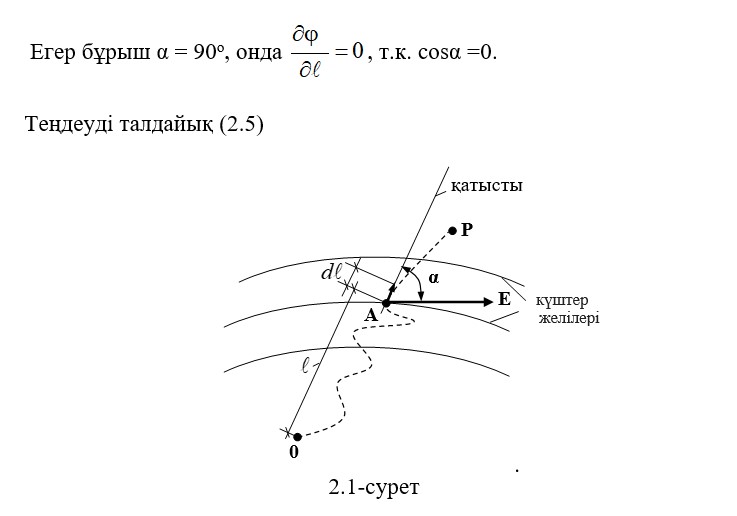
Демек, күштердің бағытына перпендикуляр бағытқа жылжу потенциалы  өзгемейді , φ = const. Осылайша, электростатикалық өрістің күштері тең потенциалды  бетіне әрқашан қалыпты болып келеді.

Егер бұрыш α = 0^о, онда cosα =1, және

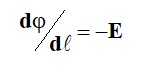
Беткейге тең потенциалдың ауыстыру бағытында ∂φ / ∂ℓ ең үлкен мәнге ие және потенциал градиент деп аталатын вектормен көрсетілуі мүмкін.

Градиентті потенциал ұзындығы бірлікке жататын және бұл өсім ең үлкен мәнге ие (бағаланған нүктелер арасындағы ең қысқа жол) бағытта қабылданған әлеуеттің өсуіне тең. Осылай жазылады:

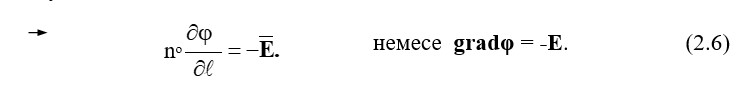
Минус белгісі потенциалды вектордың бағыты бойынша төмендейді.Тіктөртбұрышты координаттар жүйесінде (2.4)  = -E пішіні бар. Егер проекциялардың координат осіне қатысты айтатын болсақ

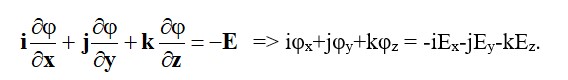
2.2 Берілгін зарядтардың таралу заңы бойынша потенциалды анықтау

 

Өріс нүкте заряды арқылы жасалады q. Өрістің потенциалын r арақашықтығында анаықтаймыз. Формула бойынша (2.3) аламыз

Өріс n нүктелік ақылармен жасалады. Бұл жағдайда птенциал еңгізу әдісімен анықталады - А нүктесінде әрбір нүкте зарядынан құрылған потенциалды алгебралық қосу

Өріс потенциалы анықталатын нүктеге дейінгі қашықтыққа қарағанда көлденең қимасы аз болғанда, зарядталған корпус (сым) арқылы жасалады. Осыда Бұл жағдайда заряд зарядтың сызықты тығыздығы бар сымның осіне шоғырландырылған деп есептеуге болады Кл/м. Бірлік ұзындығы бойынша зарядты арттыру .

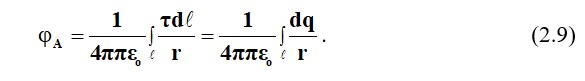
Өріс беттік заряды тығыздығы бар жер бетінде зарядталған зарядталған корпус арқылы құрылады =q/S, Кл/м². Бірлік бетіне зарядты арттыру.

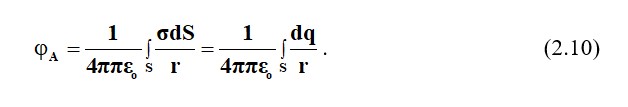
Өріс зарядталған корпусы арқылы жасалады, оның заряды көлемді көлемді көлемді жүктеме тығыздығы =q/V, Кл/м³. бойынша бөлінеді. Бірлік көлеміне зарядты арттыру .

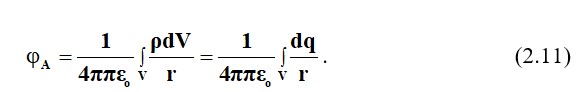
2.3 Пуассон және Лаплас теңдеулері

 

Байланыс арасындағы зарядпен және кернеу нүктеде анықталады Гаусс теоремасы. Дифференциалды түрде ол

Бұл теңдеу (2.14) Пуассон теңдеуі деп аталады, көлемнің потенциалын анықтауда қолданылады,бос емес зарядтар үшін.

Егер көлем ішінде заряд жоқ болсаρ = 0,онда біз Лаплас теңдеуін аламыз,ол бос зарядтар үшін көлемдегі потенциалды анықтау заңы үшін қолданылады

2.4 Электростатикалық өрістің шекаралық шарты

 

Өткізгіш ортаның бетінде жүргізілетін. Диэлектриктік зарядталған шекаралық бөлімді қарастырсақ (2.3-сурет).  Қарастыратын ортатын δ = 0, γ ≠ 0. Диэлектриктік ортада δ = 0, γ = 0. γ – орта мәндері. Электрөткізгіштің бетіндегі және ішіндегі ток тығыздығының векторы нөлге тең, себебі өріс электростатикалық болып табылады - электр қозғалысы жоқ (электр тогы жоқ).

δ = γЕ, бұл жерден ішкі ортадан қарастырады Е=0.

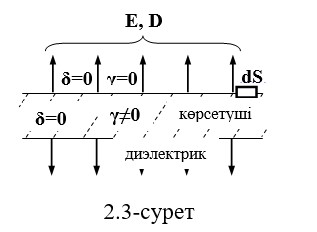
Оның E = - gradφ шығатыны, E = 0 үшін өткізгіштің барлық нүктелерінің потенциалы бірдей, φ = const. Сондықтан кернеу сызықтары E (сызықтардың сызықтары) өткізгіштің бетіне қалыпты, демек Eτ = 0.

Егер өткізгіш бетіндегі қарапайым аймақ dS таңдасаңыз және Максвелл постулаттары қолданылса, D = σ аламыз.

Вектор электр ығысу D бетінде жүргізетін дене тең беттік заряд тығыздығы σ

Шекаралық шарттар бетінің жүргізетін дене

Екі диэлектриктің  беткі бөлігі. ε₁ жәнеε₂ тұратын  екі диэлектиктің беткі бөлімінің әртүрлі диэлектриктермен қатынасын қарастырсақ (сурет 2.4).

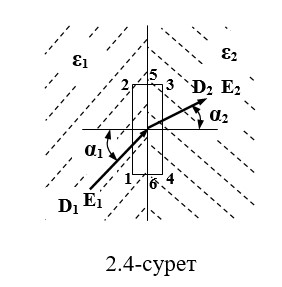
Күштің сызықтары (сызық сызықтары) қалыпты диэлектрлік α бұрышына бағытталсын (2.4-сурет). D1, D2 және E1, E2 арасындағы интерфейсіндегі сандық қатынастарды анықтаңыз. Мұны істеу үшін біз 1, 2, 5, 3, 4, 6, 1 жабық бетін таңдаймыз.

Сонда формула бойынша (2.2) бізде

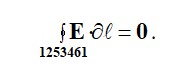
Контур бойымен интеграцияланамыз

 

Е₁sinα₁ℓ₁₂+ Е₁cosα₁ℓ₂₅+ Е₂cosα₂ℓ₅₃- Е₂ sinα₂ℓ₃₄- Е₂cosα₂ℓ₄₆- Е₁cosα₁ℓ₆₁=0.

 

ℓ₂₅= ℓ₆₁ и ℓ₅₃= ℓ₆₄, содан біз алған қысқартудан кейін

 

Е₁sinα₁= Е₂ sinα₂.                 (2.16)

Теңдеуде (2.17) шекаралық шарт бар.   

Екі ортаны арасындағы интервалда электростатикалық өрістердің векторларының тангенстік компоненттері бірдей.

Анықтау үшін сандық арақатынасын векторлар арасындағы D бөлеміз бөлімінің шекарасында екі ортаның тұйықталған беті түрінде параллелепипед, оның бейнеленген 1, 2, 3, 4, 1, 2.4-суретте.

Өйткені ішіндегі көлемінің еркін зарядтар жоқ болса, онда (1.15) аламыз

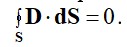
2-3 және 1-4 беттерінің беті бірдей және шексіз, ал 1-2 және 2-4 беттердің аудандары тиісінше S₁ және S₂ арқылы белгіленеді, содан кейін интегралды анықтаймыз

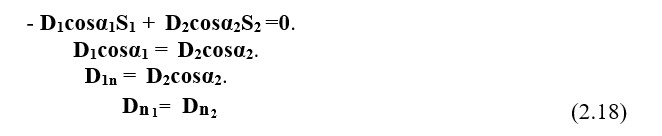
Теңдеу (2.18) – бұл шекаралық шарт:

Электростатикалық өрістегі екі мультимедиа арасындағы интервалдағы ауыстыру векторларының қалыпты компоненттері тең.

Бөлу (2.16) бойынша (2.18), біз аламыз:

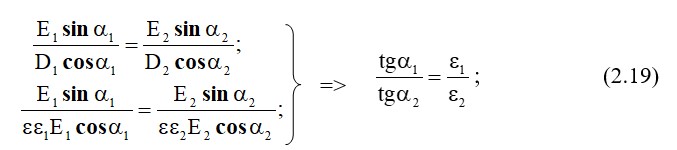
Теңдеу (2.19) екі вектор арасындағы интервалда D, E векторлары мен өткізгіштер арасындағы сандық қатынасты сипаттайды.

Алынған қатынастарды талдайық.

1. Егер E және D векторлары екі баспа құралы перпендикуляр болса, бұрышы α = 0 (сурет 2.5). Бұл жағдайда ε1 ≠ ε2 немесе D1 = D2, өйткені cosα = 1

Егер ε1> ε2, онда E2> E1. Бұл жағдайда интерфейс E векторының  қосымша күштер желісінің көзі болып табылады (2.5-сурет). Бұл электростатикалық өрісте орналасқан диэлектриктердің түрлі поляризациялау қабілетіне байланысты.

Осындай қасиет жоғары вольтты конденсаторларды, трансформаторларды оқшаулауды өндіру үшін электротехникада қолданылады.

2. Егер вектор Е және D перпендикуляр болмаса екі орта бетінде (бұрыш α ≠ 0), онда қатынасы (2.20) Е, дәлірек : ε₁Е_1n= ε₂Е_2n.

Екі диэлектриктер арасындағы интервалда электростатикалық өрістің қарқындылық векторының қалыпты компоненттері бұқаралық ақпарат құралдарының диэлектрлік рұқсат етулеріне кері пропорционалды.

 

2.5  Диэлектриктердің поляризациясы

 

Диэлектриктердің поляризациясы – электростатикалық өріс әсерінен байланысты зарядтардың реттелген орналасуы.

Гаусс теоремасынан 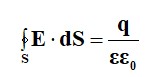Электростатикалық өрістің (ЭСӨ) қарқындылығы векторы зарядпен қозғалатын диэлектрлік қасиеттерге (дифференциалды) байланысты.

Демек, ЭҚК ішіне орналастырылған диэлектрик бейтараптылықты тоқтатады, ол поляризацияланған. Байланыстық заряд заттардың молекуласы ішінде қозғалады және олардың ішкі өрісін сыртқы өрістің векторының E бағытына бағытталған поляризациялық вектормен жасайды.

Диэлектриктің поляризация дәрежесі поляризация векторы Р арқылы сипатталады, ол сыртқы ЭСӨ кернеуінің векторына қатысты

Поляризация векторы, Р шығындар өнiмдерiнiң қосындысын бөлудiң көлемi ℓ олардың бiрлiгiшi көлемi V, алымдар арқылы алынған бөлiнiсiнiң санына тең.

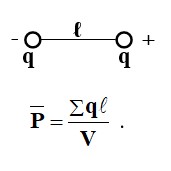
Жүктемелерді ауыстыру ішкімолекулярлық тартылыс күшіне қарсы болады.

Поляризация векторы көрсетілген ортадағы электростатикалық ауыстырудың векторын вакуумдағы электростатикалық ауыстыру векторынан қаншалықты айырмашылығы бар екенін көрсетеді

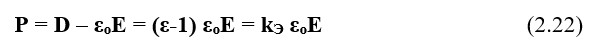
k_э = (ε-1) – диэлектриктердің поляризацияға сезімталдық коэффициенті.

 

Болашақта біз диэлектриктерді ЭТН курсының ережелерінен екі параметр бойынша - салыстырмалы рұқсат етілетін ε және электр күшіне Е_пр (диэлектрлік үзіліс орын алатын электростатикалық өрістің беріктігі) сипаттайтын боламыз.

 

2.6 Электростатиканың негізгі есептеулері. Бірегейлік шешім теоремасы

 

Электростатикалық өрістерді есептеу зарядты бөлу туралы заңға сәйкес D, E және φ мәндерін анықтауға немесе D, E және q-ге сәйкес ықтимал тарату заңына сәйкес анықталады. Электростатикалық өріс (ЭСӨ) ішінара туындыларда Лаплас немесе Пуассон теңдеулері арқылы сипатталғандықтан, көптеген шешімдер болуы мүмкін. Жалғыз шешімді алу қажет. Оны алу үшін келесі талаптарды қанағаттандыруыңыз керек:

- ЭҚК сыртқы шығындары (диэлектрикте) теңдеулерді қанағаттандыруы керек

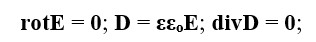
- біртекті потенциал бетінің денесі болуы керек, φ=const;

- Лаплас теңдеуінен анықталған зарядталған денелерден тыс функциялардың алынған мәндері D, E және φ үшін шекаралық шарттарды қанағаттандыруы керек.

Бұл талаптар тек қана қажет емес, сонымен бірге берілген шарттарда бір шешім алу үшін жеткілікті. Бұл ұсыныс Лаплас теңдеуінен алынған функциялардың тұтас жиынтығы, шекаралық жағдайларды қанағаттандыратын жалғыздық, шешім үшін бірегейлік теоремасын көрсетеді.

Бірегейлік теоремасынан біз екі тұжырымға келеміз:

 - егер эквипотенттік беттер жұқа өткізгіш парақпен ауыстырылса, өріс үлгісі өзгермейді;

- егер өткізгіш бетінің бір жағында зарядтардың орналасуын немесе диэлектриктерді өздігімен өзгерту мүмкін болса, сонымен бірге шекаралық жағдайларды сақтай алса, онда өріс үлгісі өткізгіш бетінің екінші жағында өзгермейді.

 

2.7 Электірлік сыйымдылық

 

Конденсатор (электрлік сыйымдылық) – диэлектриктермен бөлінген екі өткізгіш денеден тұратын құрылғы. Егер зарядтауға екі жүргізуші органға шамдар тең болса және белгіге қарсы болса, олардың арасында ЭСӨ жасалады. ЭСӨ E векторы және U өткізгіш корпус арасындағы кернеудің төмендеуі сипатталады.

С сыйымдылығы үшін аналитикалық өрнек - бұл зарядтың қабырғалардың біріне q арасындағы кернеуге U қатынасы

 

2.8  Сфералық заряд өрісі

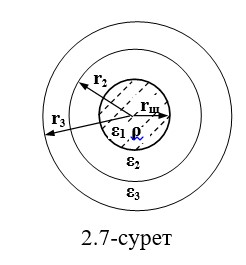
ЭСӨ радиусының r_ш сфералық зарядымен қозғалатын ЭСӨ-н қарастырайық, оның ішіндегі ρ көлемдік тығыздығы бар заряд бөлінеді. Диэлектрикалық тұрақты ε₁ шарындағы және тұтас көлемдегі өткізгіш корпус емес. Шардың айналасындағы екі оқшаулағыш қабат диэлектрлік рұқсат ε₂ және ε₃ бар.

R, ридиус функциясында D, E және φ параметрлерінің өзгеру заңын анықтау қажет.

Сфералық координат жүйесінде заңдылықтарды алу ыңғайлы.

Маңызы бар векторлардың D және E ретінде қарастыруға болады, өйткені олардың бағыты өзгермейді.

Жиынтық заряд радиусы шегінде (0) тәуелді көлемінің , оның шамасы мына формула бойынша анықталады

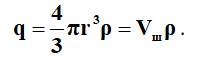
Тыс шарының радиусын (r) шамасы заряды өзгеріссіз қалады және тең:

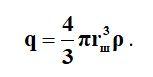
Вектордың электрлік ығысуын зерттелетін нүктеде анықтаймыз Максвелл постулаты негізінде

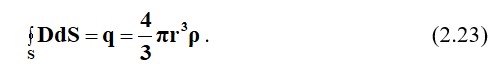
Заңына өзгерістер потенциалы ЭСӨ анықтаймыз бірі білдіру үшін градиент потенциалы

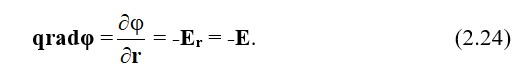
Шамасын анықтаймыз D, E и φ әртүрлі аудандарда.

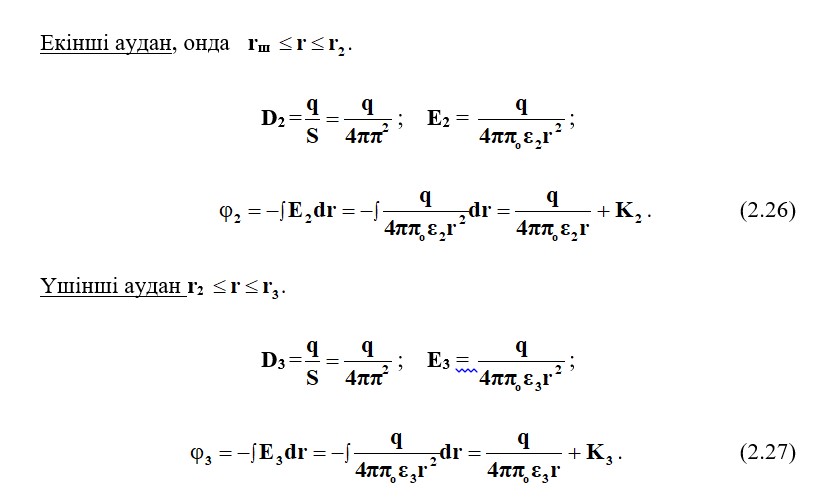
Тұрақты интегралдауды анықтау үшін К1, К2, К3 теңдеулер жүйесін,анықтау шарттары

Шамасын анықтаймыз D, E и φ әртүрлі аудандарда.

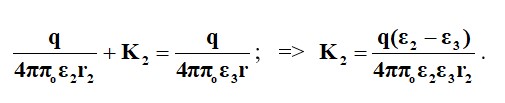
Ұқсас теңдеулерді (2.25) және (2.26) бірге шешу кезінде өрнек аламыз К₁

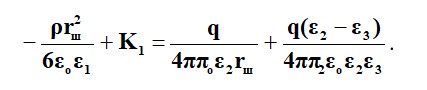
2.25 ÷ 2.27 теңдеулерін талдаудан сфералық заряддан тыс потенциалдың өзгеруі нүктелік зарядтың немесе зарядтың шардың ортасындағы шоғырланған потенциалын өзгерту ретінде қарастырылуы мүмкін.

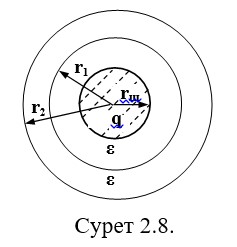
Біз сфералық заряддан тыс жерде орналасқан екі сфералық беттердің (сурет 2.8) потенциалын радиустары r₁ және r₂ арқылы анықтаймыз.

Бірінші және екінші беттердің потенциалдары тиісінше тең болады:

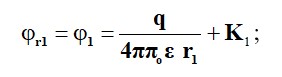
Тұрақты интегралдау К1 және К2 айналады нөлге тең, егер қабылдау кезінде r = ∞, φ =0.

Біркелкілік заңына сәйкес біз эквпотенциалды беттерді r₁  және r₂ радиустарымен алмастырамыз

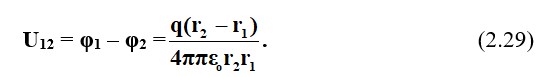
(2.29) бойынша электростатикалық өріске орналастырылған өткізгіш беттердің зарядталуы керек.

2.8-суреттегідей, диэлектриктермен бөлінетін екі өткізгіштің беті сфералық конденсатор болып табылады.

Егер өткізгіш беттерге тең шамалар мен сигналдардың кернеуі туралы ақпарат берілсе, олардың арасындағы кернеу формула бойынша анықталады (2.29) және арадағы сыйымдылық:

Жүргізетін беті қоршалған зарядталған шар келесі параметрлерге ие сфералық конденсатор болып табылады

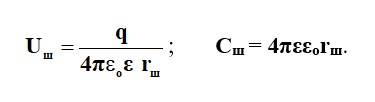
2.9 Электрлік дипольдік өріс

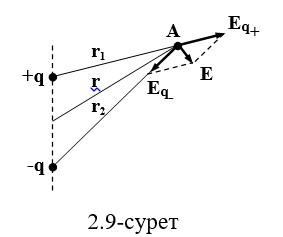
Электрлік диполь – бұл екі қарама-қарсы зарядтардың + q және -q зарядтарының жүйесі.

E күші және ықтимал φ белгілі бір нүктесінде А (2.27) сәйкес суперпозициялар әдісімен анықталады.  

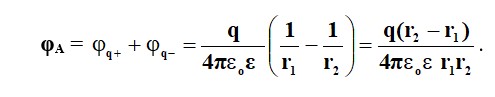
2.10 Екі біркелкі зарядталған беткі өткізгіштің өрісі

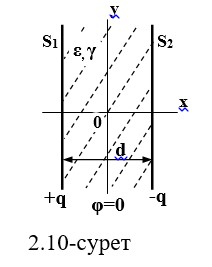
Келесі параметрлермен бір-бірінен d қашықтықта орналасқан екі жұқа өткізгіш беттерді қарастырамыз

Оның (2.31) параллельді жүргізетін жазықтықтардың арасында орналасқан өрістің әрбір нүктесінде D және E векторлары сәйкесінше бірдей мәнге ие, сондықтан өріс біртекті болып табылады.

Гаусс теоремасына сәйкес және шекаралық жағдайларға сәйкес, Е өткізгіш ұшақтарға перпендикуляр бағытта (x-ось бағыты бойынша) болады:

Біз заряд бетінің тығыздығын U кернеуінің кернеуі тұрғысынан білдіреміз және (2.34) алынған өрнекшені алмастырамыз:

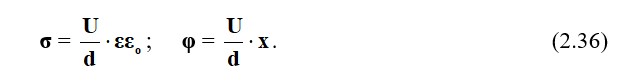
Теңдеу (2.36) теңдеудің теңдеуі болып табылады (тең әлеует беті), ол параллель беттерге параллель бірдей қашықтықта тартылады.

        E = f (x) және φ = f (x) тәуелділіктерінің кестесі 2.11-суретте келтірілген.

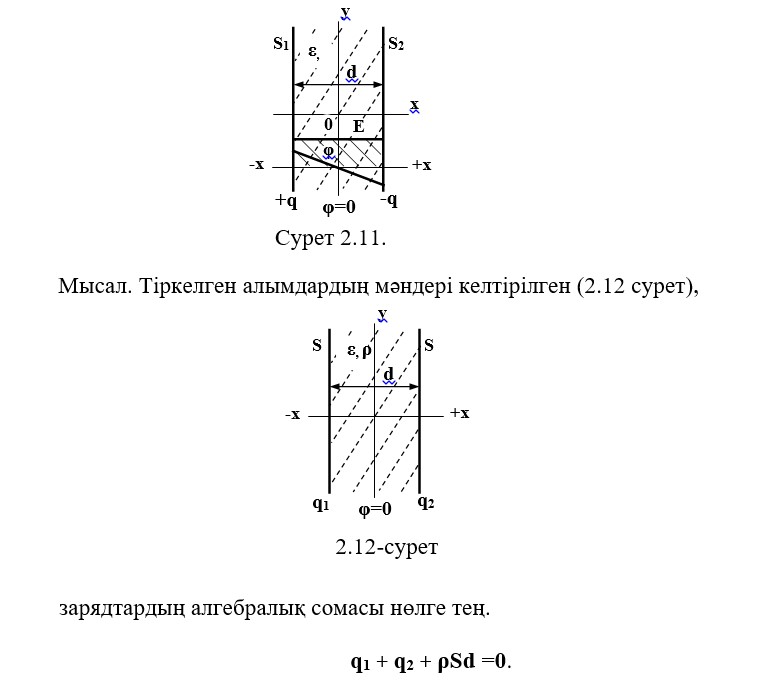
Пуассон теңдеуін қолданумен x функциясының E және φ параметрлерінің өзгеру заңын анықтаймыз.

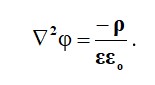
Тіктөртбұрышты координат жүйесінде y және z осі өткізгіш тақталар S-мен сәйкес келеді, сондықтан φ координаттар y және x-ға тәуелді емес. Біз:

2.11 Зарядталған осьтің өрісі

 

Датчиктің диаметрі оның ұзындығынан әлдеқайда аз болса, зарядталған осьтің астында жіңішке, ұзын зарядталған өткізгіш.

D, E және φ өрістерінің қашықтықтан r-ге дейінгі оське дейінгі функциясының өзгеру заңын анықтаңыз (2.13-сурет).

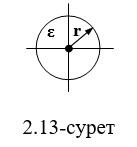
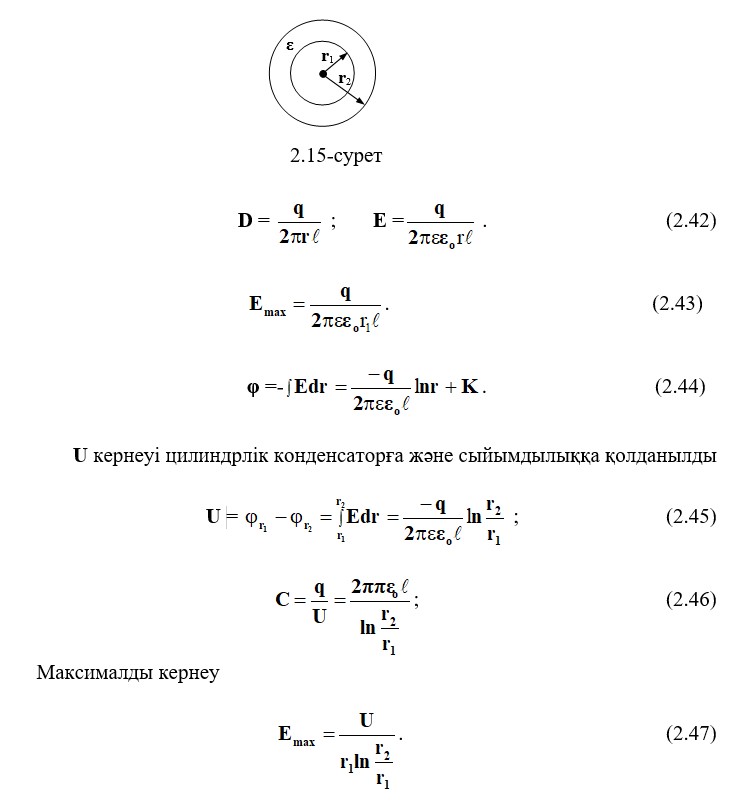
2.12 Цилиндрлік конденсатор өрісі

 

Өрісінде зарядталған осінің мәндері екі цилиндрлік беттің радиустары r₁ және r₂,

 

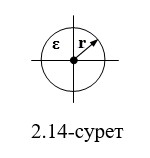
D, E және φ өрістерінің параметрлерінің өзгеру заңы өзгермейтін беттердің жұқа өткізгіш беттерімен ауыстырылған жағдайда өзгермейді. Нәтижесінде цилиндрлік конденсаторды, ішкі бетінің заряды q1 = σ1ℓ, сыртқы q2 = σ2ℓ аламыз. D, E және φ өрістеріндегі айырымдық беттердің параметрлерін өзгерту туралы заң теңдеулермен анықталады (2.40) және (2.41).

2.13 Параллельді зарядталған екі осьтің өрісі

 

Шегерілген зарядталған екі осьті қарастырамыз  и , бір-біріне тең қашықтықта орналасқан 2а (2.16-сурет). Белгіленген осьтердің өрісінде біз нүкте аламыз М суперпозициялар әдісімен біз осы тармақтың потенциалын анықтаймыз.

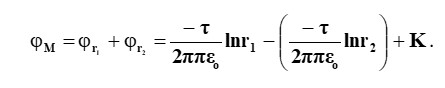
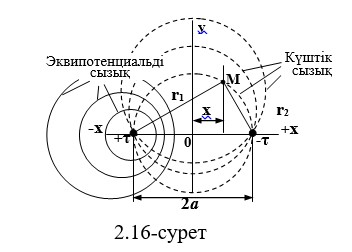
Интеграциялық тұрақты K келесі шарттардан анықталады:r₁=r₂, φ=0 => К=0.

Нәтижесінде эквипотенциалды бетінің (шеңбер) теңдеуін аламыз.

Орталығы эквипотенциальной шеңбер келмесе орталығы қимасының осі. Эквипотенциальные шеңбердің өзара перпендикуляр түйісетін бастап күш сызықтары.янии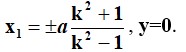

2.14 Екі сымның өрісі және сыйымдылығы

             

Екі сымды желіні қарастырайық (2.17-сурет).

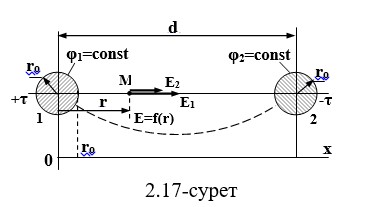
d>>r деп санауға болады, бұл орталықтар электрлік осьтердің геометриялық және орталықтар қимасы дөңгелек сымы сәйкес келеді.

Заңдар өзгерісіне сәйкес Е және φ функциясынан анықтаймыз r.

Сымдар орталықтарын жалғайтын желіде біз алыс қашықтыққа M нүктесін аламыз

 

r сол жақ сымнан және суперпозиция әдісімен Е_м керілісін анықтаңыз.

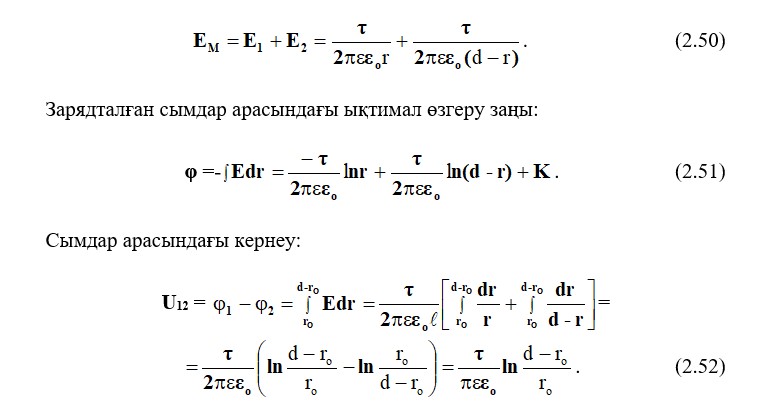
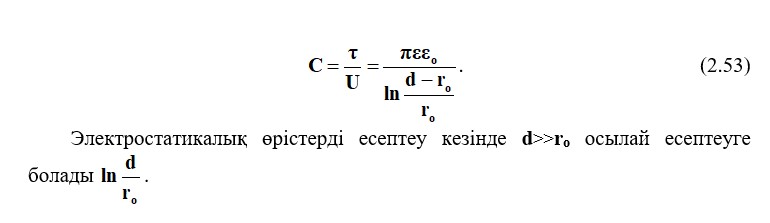
Екі сымды сызықтың бірлік ұзындығы бойынша сыйымдылығы:

 

2.15 Айнадай кескіндердің әдісі

 

Бұл екі немесе одан да көп диэлектриктермен тиісті геометриялық пішіні немесе өріс өткізетін беті шектелген өрістерді есептеген кезде, қосымша шығындар енгізілген, олардың мәндері мен орналасуы таңдалған етіп, электростатикалық өрістерді (ESP) есептеу кезінде жасанды әдіс. шекаралық шарттарды қанағаттандыру. Егер медиа арасындағы интерфейс тегіс болса, онда берілген зарядтардың айналы кескіндері орналасқан жерде қосымша төлемдер пайда болады.

Бұл әдіс шешім үшін бірегейлік теоремасының салдары болып табылады.

Q = τ (зарядталған ось) зарядымен жасалған өрісті қарастырайық. Заряд екі параметрдің интерфейсінен жоғары, олардың параметрлері ε1 және ε2 (сурет 2.18, а). Бірінші және екінші бұқаралық ақпарат құралдарындағы өрісті есептеу үшін айнадағы кескін әдісін қолданамыз. Осы мақсатта бірінші және екінші медиа бір диэлектрик ε₁-ке толтырылған деп санаймыз. Екінші ортадағы диэлектрлік константаның әсері екінші ортаға бөлінген зарядтың τ-ның айна бейнесі орналасқан (§ 2.18, б) жобалық жүктемені τ '= q енгізумен ескеріледі. Сонда бірінші және екінші медиа диэлектрик ε₂ толтырылған деп есептейміз. Алғашқы ортаны екінші зарядтың әсері осы зарядтың орнында орналасқан τ '' дизайнерлік зарядты енгізумен ескеріледі (2.18-сурет, с).

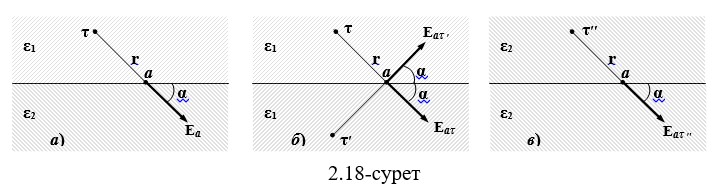
Трансформациялар ε₁ және ε₂ зарядтары мен рұқсат етулерімен τ 'және τ' есептелген шығындар арасындағы сандық қатынас үшін теңдеулерді алу үшін орындалады.                   

2.18-суреттегідей, нүктедегі өріс күші келесідей болады: 2.18-суреттегідей, нүктедегі өріс күші келесідей болады

Теңдеулер (2.56) ЭСӨ параметрлерін анықтаған кезде жобалық алымның қандай мәнін енгізу керек екенін көрсетеді. Бұл жағдайда, сурет 2.18, b диаграммасы ЭСӨ параметрлерін ε₁ ортасында және 2.18-суреттегі схемадағы E₂ параметрлерін анықтау үшін ғана қолданылады, бұл - ортада ε₂.

Егер ЭСӨ құрайтын зарядты өткізетін бет үстінде болса, онда D, E және      φ = f (r) параметрлерін өзгерту заңын анықтау үшін есептелген зарядты шамаға тең және керісінше көрсетілген зарядқа айна бейнелеу нүктесіне қоямыз, Диэлектрик берілген ε.

2.16 Жақын орналасқан беткі зарядталған жүйесінде потенциальді коэффициентті анықтау

 

Екі зарядталған осьтерімен біртекті ортада құрылған ЭСӨ-ді қарастырыңыз. Біз екі параллельді бөлек зарядталған осьтермен қозғалған өрістегі М нүктесін таңдаймыз.

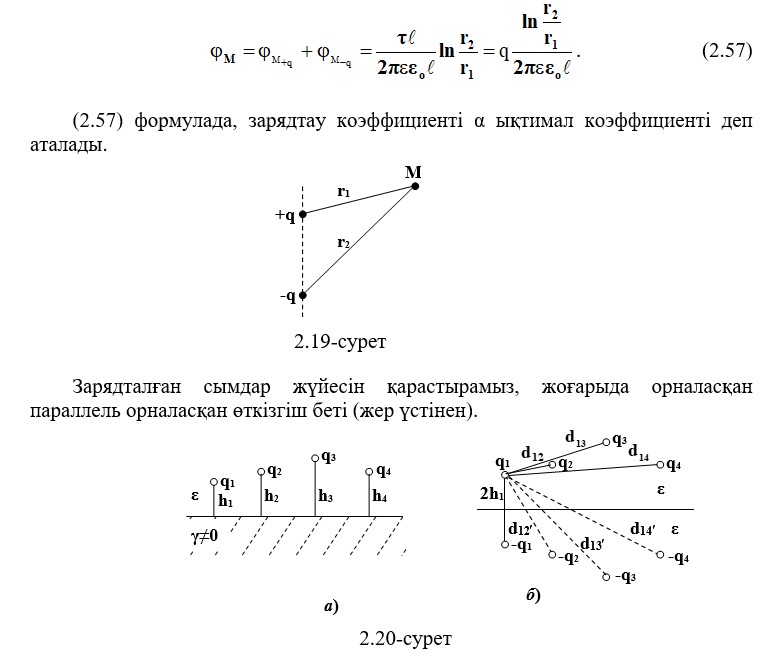
2.20-суретте радиусы бар, оң зарядты сым жүйесі бар. Параллель сымдар жер үстінен орналасқан. Сымдардың радиусы сымдар мен жер асты суспензиясының биіктігі арасындағы қашықтықтан әлдеқайда аз. Соңғы жағдай геометриялық және электрлік зарядтау орталықтарының (зарядталған осьтер ретінде сымдар) сәйкес келетінін болжауға мүмкіндік береді. Бірінші сымның әлеуетін анықтаймыз: q1 = τ1ℓ. Айнадай кескіндердің әдісін қолдану арқылы біз дизайнерлік шығындарды енгізіп, өткізетін бетін ауыстырамыз (2.20, б).

Теңдеулерге сәйкес (2.57) біз:

Теңдеулер жүйесі (2.58) Максвелл теңдеулерінің бірінші тобы деп аталады, онда: α₁₁, α₂₂, α₃₃, α₄₄ – ішкі потенциалды коэффициенттер;

  α₁₂, α₁₃, α₂₃, α₃₄  және т.б.– өзара потенциалды коэффициенттер.

Барлық ықтимал коэффициенттер тек денелердің геометриялық өлшемдеріне, олардың өзара орналасуына және ортаны диэлектрлік жол берілуіне байланысты. Олардың өлшемі 1, Фарад бөлінген. Олардың бәрі оң. Мысалы, α₁₁ саны бірінші сымның әлеуетіне тең, оның заряды бірге тең болғанда және қалған сымдардың заряды нөлге тең болады.

 

2.17 Зарядтардың арасындағы және потенциальдың зарядталған жүйедегі байланысын анықтайтын теңдеу

 

Максвелл теңдеулерінің бірінші тобы белгілі сымдардың сымдардың әлеуетін анықтауға мүмкіндік береді. Егер сымдардың потенциалы белгілі болса, онда шығындарға қатысты теңдеулер жүйесін (2.58) шешсек, біз (2.59) - Максвелл теңдеулерінің екінші тобы аламыз:

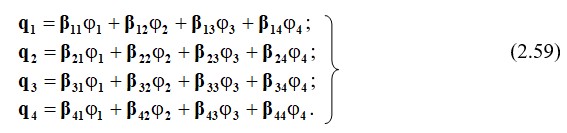
мұнда β₁₁, β₂₂, β₃₃, β₄₄ – меншікті сыйымдылық коэффициенттері;

           β₁₂, β₁₃, β₂₃, β₃₄  және т.б. – өзара сыйымдылық коэффициенттері.

 

 Сыйымдылық коэффициенттерінің өлшемі - Фарад. Ықтимал сыйымдылық коэффициенттері әрдайым теріс, дұрыс болып табылады.

β-ның сандық мәндері Максвелл теңдеуінің (2.58) бірінші тобынан табылған 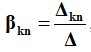, мұнда Δ теңдеулер жүйесінің негізгі анықтаушысы (2.58), ал Δ_kn - k-ші қатарын және Δ-дағы n-бағанды жою және (-1) ^{k + n} арқылы көбейту арқылы алынған алгебралық қосымша. Машиналық тәжірибеде n-зарядталған органдардың жүйесінде көбінесе зарядтар мен потенциалдар болмайды, әлеуетті айырмашылық, атап айтқанда, сымдар мен сым мен жер арасындағы кернеу беріледі.

N сымдар жүйесіндегі кернеулер мен потенциалдар арасындағы қатынастарды қарастырайық. Мұны істеу үшін теңдеулерді (2.59) түрлендіреміз және мыналарды аламыз:

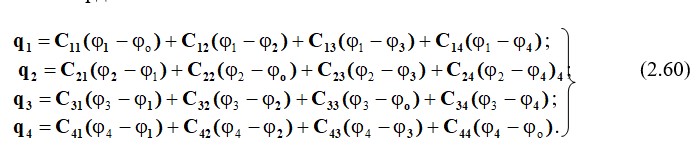
Теңдеулер (2.60) Максвелл теңдеулерінің үшінші тобы болып табылады.

С₁₁= β₁₁+ β₁₂+ β₁₃+ β₁₄ – жеке бөлшектей сыйымдылығы. С_kn= -β_kn – өзара ішінара сыйымдылық. Ішінара қуаттылық үнемі оң. φ_o=0 –жердің потенциалы.

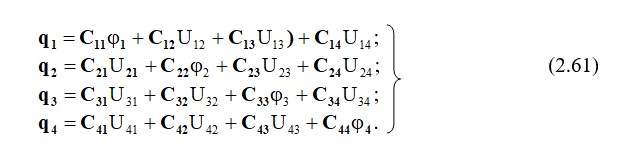
1-мысал. Заряд + q сым жердің үстінен орналасқан (сурет-2.21, а).

 

Сымның потенциалын анықтау қажет, арасындағы сыйымдылық сымдар мен жұмыс қабілеттілігі.

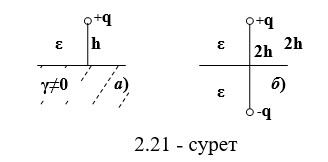
Айнадай кескіндердің әдісін қолдану арқылы біз өткізгіш бетті орта ε және қосымша зарядпен -q ауыстырамыз (2.21-сурет, б). Біз:

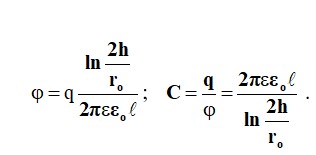
2-мысал. q₁ = + q және q₂ = -q зарядтары бар екі сым жердің үстінде орналасқан. Сызықтың ұзындығы ℓ, радиус - r_o, сымдардың d арасындағы қашықтық, сым сымының h₁ және h₂ биіктігі (2.2.2, a).  Жұмыстың сыйымдылығын C_p, C₁₂ сымдары мен сымдар C₁₁, C₂₂ қатысты сымдар арасындағы сыйымдылықты анықтау қажет.

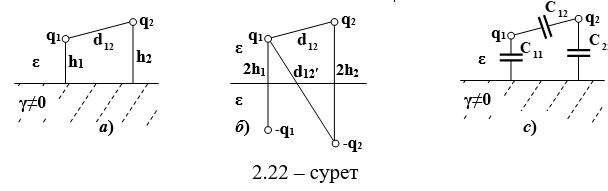
Айнадай кескін әдісінің көмегімен есептеу схемасын құрастырамыз (2.2.2, б) және Максвелл теңдеулерінің бірінші тобына сәйкес теңдеулер жүйесін құрастырамыз.

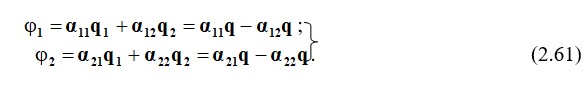
Сондай-ақ, q₁ + q₂ = 0 теңдеуі бар; өткізбейтін беті бар сымдар электрмен қосылмаған.

Сымдар арасындағы кернеу U₁₂ =φ₁ –φ₂.

Жұмыс істеу сыйымдылығы С_раб=q/U (екі сымды жүйенің сыйымдылығы).              

Теңдеулер жүйесінен (2.61) біз U₁₂ және С_rab кернеуін анықтаймыз:

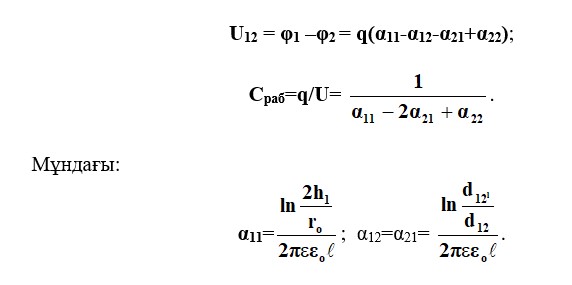
Алынған α₁₁ және α₁₂ мәндері, ақырында, нәтиже береді:

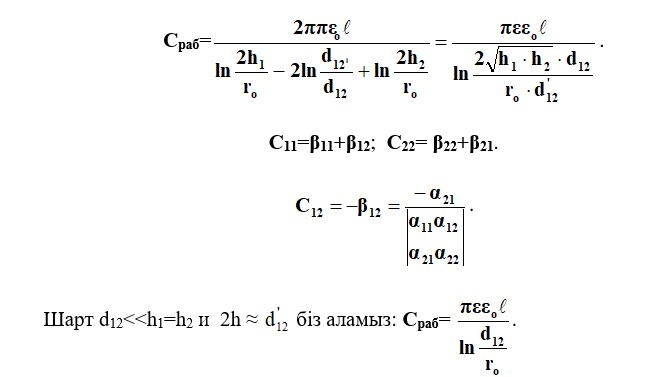
Мысал 3. Екі сымды сызық (2.22, a) үшін келесі мәндер берілген: d₁₂ = 2 м; h₁ = h₂ = 6 м; ro = 10 мм; ℓ = 16 км; ε = 1; | + q₁ | = | -q₂ |; φ₁ = 15 кВ;

φ_o = 0; φ₂ = -15 кВ. Ішінара және жұмыс істейтін сыйымдылықты, зарядтау мөлшерін q₁, q₂, U₁₂ кернеуін анықтау қажет.  

1 Максвелл теңдеулерінің бірінші тобын жазамыз:

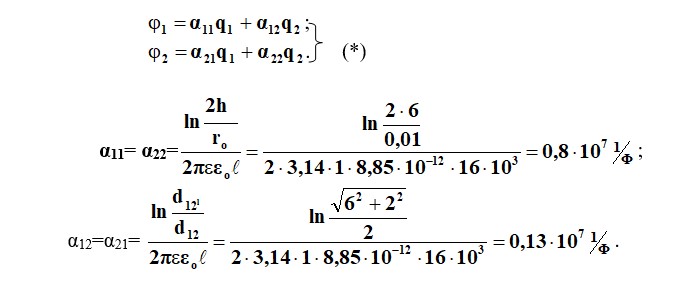
2 Максвелл теңдеулерінің екінші тобынан сыйымдылық коэффициенттерін анықтаймыз

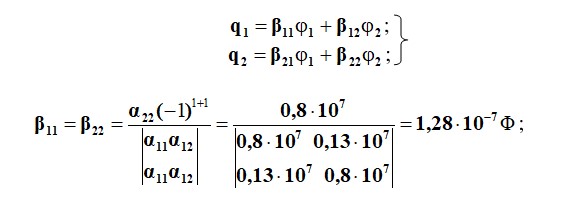
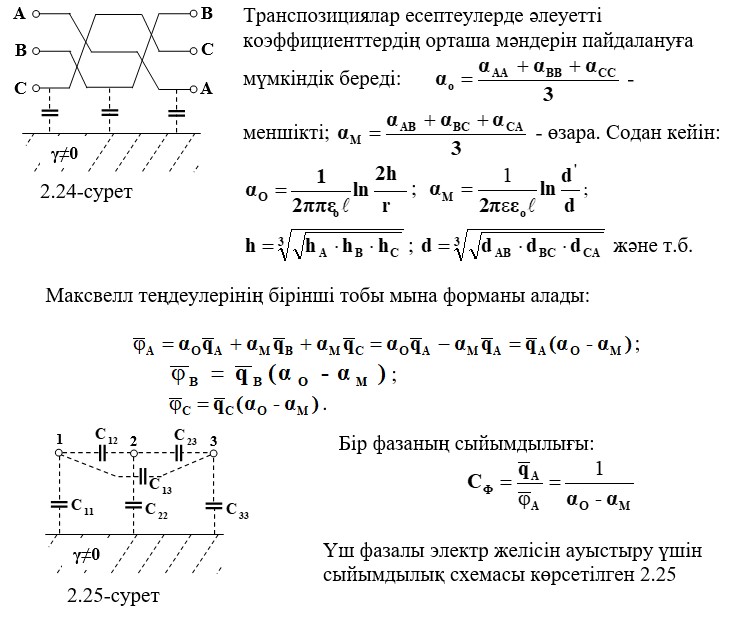
2.18 Үш фазалы электртарату сызығының сыйымдылығы

 

Максвелл теңдеулерінің барлық үш тобы желілік ұзындығы ℓ толқын ұзындығынан әлдеқайда аз болса, өнеркәсіптік жиілікте (50 Гц) жұмыс істейтін нақты электр желілерінің сымдарының сыйымдылығын анықтау үшін пайдаланылуы мүмкін λ, яғни ℓ<<λ, мұнда λ=υ/f =υ·T=6000 км. Бұл жағдайда желінің барлық нүктелерінде ауытқулардың фазасы бірдей, бұл әрқайсысында уақытты электростатикалық деп қарастыруға мүмкіндік беретін бірдей. Потенциалдардың бірден-бір құндылығы зарядтардың лездік мәндері арқылы жазылады, олар синусоидальдық заңға байланысты өзгереді

d_AB^׳,  d_BC^׳,  d_AC^׳ – әртүрлі фазалардың айна бейнесінің қашықтығы; Тіпті барлық биіктіктегі үш фазаның сымдарымен орналасса да, олардың орналасуындағы (ортасында немесе шеттерінде) айырмашылық жүргізуші бетінің (жердің) болуына байланысты симметрияның пайда болуына әкеледі. Сымдардың сыйымдылығы бірдей емес, ал сызықтардың ұштарындағы фазалардың әлеуеті ассиметриялық үш фазалы кернеулер жүйесін құрайды.Сызықтардың ұштарында симметриялық жүйені құру үшін сымдардың транспозициясын қолданыңыз (сымдар фазаларының орнын өзгертіңіз).

2.19 Білім сапасын тексеру үшін тесттік тапсырмалар

 

№ 2.1 Гаусс теориясының формуласын көрсетіңіз

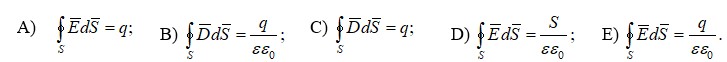
№ 2.2 Мына берілген сурет бойынша А нүктесінің зариядын және арақатынасының сомасын анықтау керек.

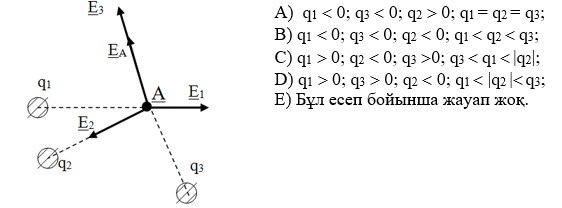
№ 2.3 Шардың орталығынан сырттай әлеуетті есептеу үшін формуланы, r қашықтықта q заряды бар, шексіз алыс нүктенің әлеуетін нөлге дейін есептеу арқылы шығарыңыз

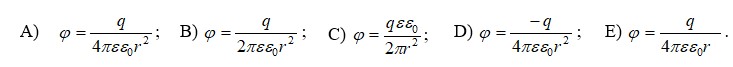
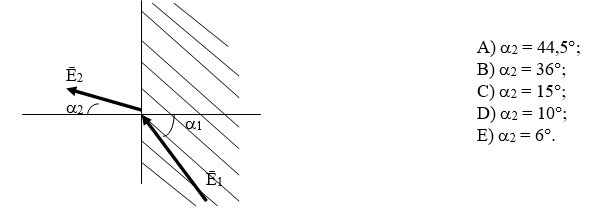
№ 2.4  Егерде a₁ = 60°болса, аралықта Е аумаққа ауа кіретін a₂ бұрышты табу керек.

№ 2.5 Жер бетіне параллельді бойлай сағасындағы біртұтас сымның әлеуетін анықтаңыз. Сымның радиусы r₀.

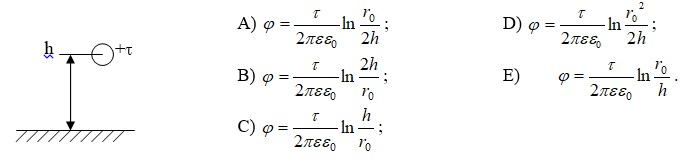
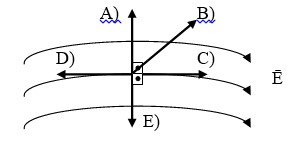
№ 2.6 Берілген суреттегі аумақтың grad j бағытын көрсетіңіз

№ 2.7  Берілген E (x) көп қабатты жалпақ конденсатордың тәуелділігі арасындағы e₁ , e₂, e₃ қатынастарын табыңыз.

№  2.8  Қай суретте соленоидиальды аумақ көрсетілген?

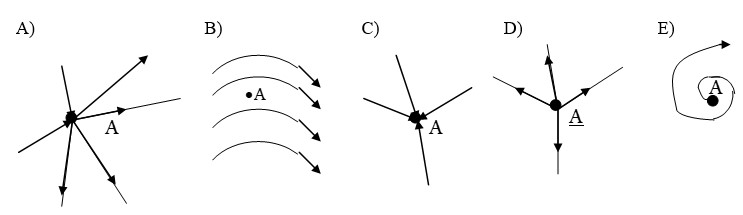
№  2.9  M нүктесіндегі өрістің суретінен зарядтардың шамаларын және белгілерін табыңыз.

№  2.10  Ауыстырылған D радиусы шарының орталығынан r қашықтықта ауыстыруды табыңыз.

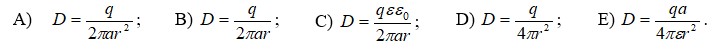
№  2.11  Көп қабатты изоляциясы бар цилиндрлік конденсатор үшін E (r) тәуелділігі берілген.  e₁, e₂, e₃ теңдігін табу керек.

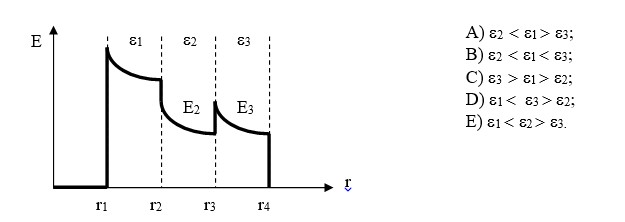
№ 2.12 Электростатикалық өрістегі екі диэлектриктің шекарасында шекаралық жағдайларды көрсетіңіз.

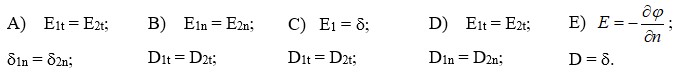
№ 2.13 Доптың сыртында және ішінгде вакуум бар. Шардың орталығында электростатикалық өрістің күші қандай?

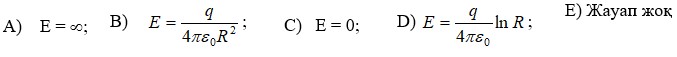
№ 2.14  Арасындағы ара қатынасын табыңыз e₁, e₂ және e₃ үш қабатты диэлектриктегі электростатикалық күш күштерінің сызбасына сәйкес

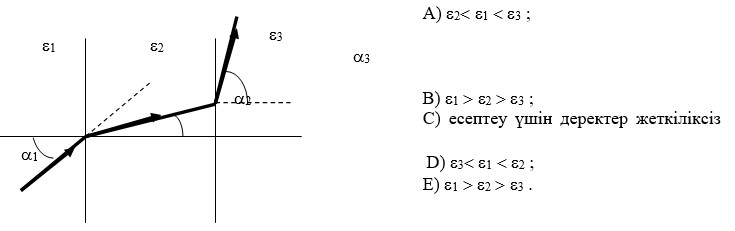
№ 2.15   Өрістің суретінен тең әлеуеттің сызығын көрсетіңіз.

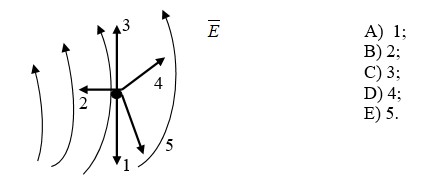
№ 2.16   Дұрыс тұжырымдаманы табыңыз.

1. Теңдік потенциал теңдеуі , кернеулік сызықтарымен 90 градус бұрышпен қиылысады
2. Теңдік потенциал теңдеуі , кернеулік сызықтарына қарсы бағытта
3. Теңдік потенциал теңдеуі , кернеулік сызықтарымен 90 градус бұрышпен қиылысады
4. Теңдік потенциал теңдеуі , кернеулік сызықтарына қарсы бағытта
5. Теңдік потенциал теңдеуі , кернеулік сызықтарымен қиылысады

 

№ 2.17  Дұрыс тұжырымдаманы табыңыз:

1. Потенциал градиенті – бұл ұзындық бірлігіне қатысты және потенциал өсімі ең аз мәнге ие болатын бағытта таралатын өсім

.

1. Потенциал градиенті – бұл ұзындық бірлігіне қатысты және потенциал өсімі ең аз мәнге ие болатын бағытта таралатын өсім

.

1. Потенциал градиенті – бұл ұзындық бірлігіне қатысты және потенциал өсімі ең үлкен мәнге ие болатын бағытта таралатын өсім

.

1. Потенциал градиенті – бұл ұзындық бірлігіне қатысты және потенциал өсімі ең үлкен мәнге ие болатын бағытта таралатын өсім

.

1. Потенциал градиенті – бұл ұзындық бірлігіне қатысты және потенциал өсімі ең үлкен мәнге ие болатын бағытта таралатын өсім кернеулік өрісімен бағыттас. 

.

 

№ 2.18  Дұрыс тұжырымдаманы табыңыз:

1. Кез-келген құйынсыз өріс формуласымен сипатталады, және потенциалды болып табылмайды, демек әр нүктесінскалярлық функциясымен сипаттауға болмайды.
2. Кез-келген құйынсыз өріс формуласымен сипатталады және потенциалды болып табылады демек әр нүктесінскалярлық функциясымен сипаттауға болады.
3. Кез-келген құйынсыз өріс формуласымен сипатталады және потенциалды болып табылмайды, т демек әр нүктесінскалярлық функциясымен сипаттауға болмайды.
4. Кез-келген құйынсыз өріс формуласымен сипатталады және потенциалды болып табылады, демек әр нүктесінскалярлық функциясымен сипаттауға болады.
5. Кез-келген құйынсыз өріс формуласымен сипатталады және потенциалды болып табылмайды, демек әр нүктесінскалярлық функциясымен сипаттауға болмайды.

 

№ 2.19  Дұрыс тұжырымдаманы табыңыз:

1. Стационарлы электрлік өріс –тізбектегі электр токтары мен ЭҚК әсерінен пайда болған өріс.
2. Стационарлы өріс осы аумақта магниттелген дене болған жағдайда зарядтар әсерінен пайда болады.
3. Электрлік өріс қарастырылып отырған аумақта магниттелген дене болмаған жағдайда бақылаушыға қатысты тыныштықта тұрған зарядтар әсерінен пайда болады.
4. Электростатикалық өріс қарастырылып отырған аумақта магниттелген дене болған жағдайда бақылаушыға қатысты тыныштықта тұрған зарядтар әсерінен пайда болады.
5. Стационарлы өріс осы аумақта магниттелген дене болмаған жағдайда зарядтар әсерінен пайда болады.

 

№ 2.20   Дұрыс тұжырымдаманы табыңыз:

1. A) Айнадай кескіндердің әдісі жердің өрісін ескеруге мүмкіндік береді, ал қысқа тұйықталу орнында жердегі заряд ауаның ішіндегі айна бейнесімен ауыстырылады.
2. B) Айнадай кескіндердің әдісі индукцияланған зарядтардың диэлектриктердегі сыртқы өрісіне зарядтың айна бейнесі арқылы оның белгісінің өзгеруімен ауыстыруға мүмкіндік береді.
3. C) Айнадай кескіндердің әдісі зарядтың белгісінің өзгеруімен сымның айна бейнесі арқылы оның бетіне шығарылатын зарядпен өткізгіш ортаны ауыстыруға мүмкіндік береді.
4. D) Айнадай кескіндердің әдісі зарядтың белгісін сақтай отырып, сымның айна бейнесі арқылы оның бетіне шығарылатын зарядтармен өткізгіш ортаны ауыстыруға мүмкіндік береді.

Е) Дұрыс жауабы жоқ.

 

2.20 Дұрыс жауаптар коды

 

№ сұрақ	Сұрақтың жауабы	№ сұрақ	жауабы	№ сұрақ	жауабы	№ сұрақ	жауабы
2.1	E	2.6	D	2.11	E	2.16	A
2.2	D	2.7	B	2.12	D	2.17	D
2.3	E	2.8	B	2.13	C	2.18	B
2.4	D	2.9	A	2.14	A	2.19	C
2.5	B	2.10	D	2.15	B	2.20	C