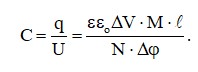4.1  Тұрақты ток магнит өрісінің негізгі теңдеулері

 

Электромагниттік өріс теңдеулер жүйесінде (1.27) магнит өрісі теңдеулерді сипаттайды:

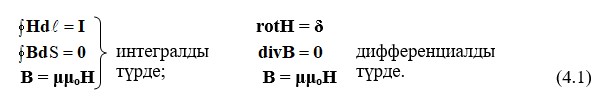
Жүйенің бірінші теңдеуі (4.1) магнит өрісінің потенциалды емес, құйынды екенін көрсетеді. Демек, егер δ ≠ 0 болса, әлеуетті градиент тиісті H векторына тең емес.

Дегенмен, δ = 0 ортасында магнит өрісі скаляр магниттік әлеуетімен сипатталуы мүмкін, олар үшін gradφm = -H. Құрамдас бөлік кез келген бағытта H векторы (HN) бірлік ұзындығына (∂ℓ) қатысты берілген бағытта магниттік әлеуеттің төмендеуіне тең.           

4.2  μ-лары әртүрлі екі ортадағы шекаралық шарт

 

Егер магниттік индукция B (магниттік күш сызықтары) сызықтары әртүрлі μ екі магниттік ортаны интерфейсін қиып алса, онда B сызығының интерфейсінде олардың бағыты өзгереді.

Екі орта арасындағы магниттік индукциялық вектордың қалыпты компоненттері, В.

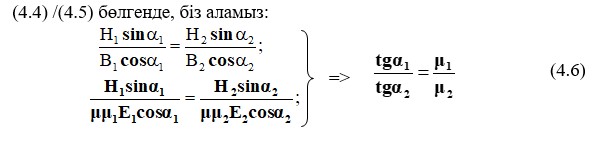
Теңдеу (4.6) екі медиа арасындағы интервалда B, H және магнит өткізгіштерінің арасындағы сандық қатынасты сипаттайды.

 Ауа үшін  μ_в≈1, ферромагниттік орта үшін μ_ф>>1 мәніне тең, ол tgα_в<< tgα_ф, яғни  B сызығы металлдың бетіне қалыпты.

4.3 Айна кескінінің әдісі

 

Бұл әдіс әртүрлі магниттік өткізгіштері бар екі мультимедиа интерфейсінің маңында орналасқан ток өткізгіштермен жасалған өрістерді есептеу үшін пайдаланылады.

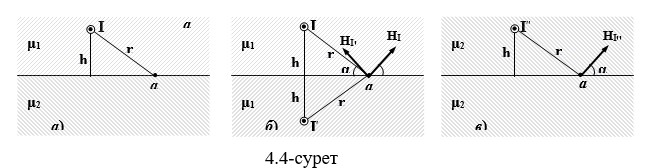
Берілген және жалған токтар арасындағы байланысты алу үшін біз нүктені және екі орта арасындағы (4.4, а) және H және В векторларының шекаралық шарттарын қолданамыз.

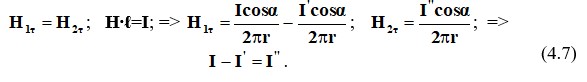
Вектордың қалыпты компоненттері екі ортада тең:

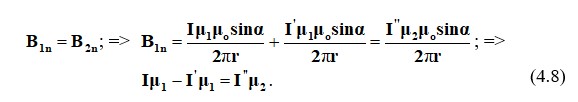
Біз теңдеудің екі жағын (4.7) μ₂ арқылы көбейтеміз және оны біріншіден екіншісін шегеру арқылы 15.8 теңдеуімен бірге шешеміз немесе оларды аламыз:

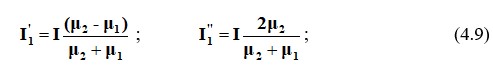
Егер ток бар ток өткізгіш және ферромагниттік ортаға жақын орналасқан болса  μ₂>>μ₁, а I^’≈I, I^’’≈2I.

 

4.4 Тұрақты токтағы магниттік өрістің векторлық потенциалы

 

Магнит өрісін есептеуді оңайлату үшін жасанды сандық - магнит өрісінің векторлық потенциалы енгізілді, А. Бұл жағдайда магниттік индукция В векторы векторлық потенциалдың құйындысы ретінде ұсынылған, B = rotA.

Осындай ауыстыру кезінде вектордың әлеуеті А - электр өрісінің ықтимал φ-ге ұқсас координаттардың функциясы. Осындай ауыстырудың себебі магниттік индукция сызықтарының үздіксіздігі болып табылады В,(divB=0).

Шыққан мәні divrotA = 0.

Бұл шартты қанағаттандыратын A шамасын анықтаймыз.    

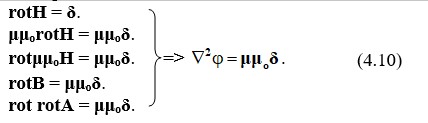
(4.10) теңдеуі – магниттік өріс үшін Пуассона теңдеуі         

4.5 Ток элементінің магниттік өрісі
       Дифференцирленген теңдеудің (4.13)  

Кернеуді  Н,акғымдық элементпен қарқындылықты анықтаймыз

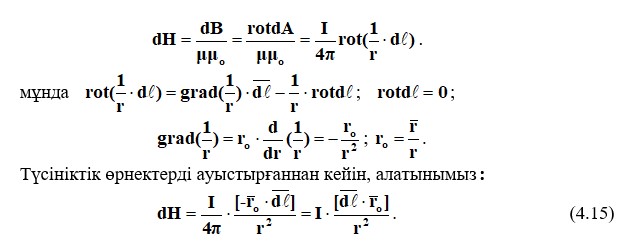
Теңдеу (4.15) – Био-Савара-Лаплас заңы

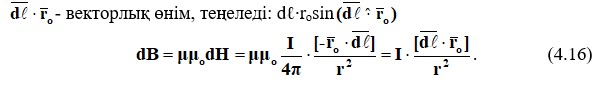
Биот-Саварт-Лаплас заңы кез-келген күрделі пішіндегі өткізгішпен жасалған өріс параметрлерін есептеуге мүмкіндік береді. Толық ток заңына сәйкес, қалыпты пішінді өткізгіштер шығаратын В, Н өрісінің параметрлерін есептеу ыңғайлы. Ағымдағы ағымдардың ортасына қарай, ағымдық элемент Idℓ, 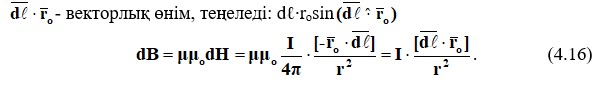- сұйық өткізгіштер үшін.

4.6  Магнит ағынының векторлық потенциал арқылы көрінісі 

Магниттық ағын Ф белгілі бір бетке S тең

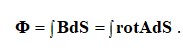
Стокс теоремасына сәйкес тұжырым аламыз

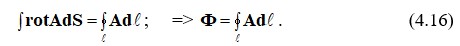
нциалдың айналымына  А  тең болады S

Есептеу үшін Ф арқылы анықтау В бетінің барлық нүктелерінде S аламыз. Есептеу барысында Ф векторлық потенциал арқылы А-ның А контурде ғана болатының білуіміз тис, шектік беті S, бұл есептеуді азайтады.

 

4.7 Био-Савара-Лапласс заңын магнит өрісінің күшін есептеуге қолдану

 

а) Тогы бар сызықты өткізгішті магниттік өріс.

Сурет.4.7 осы мәндерге сәйкес: ℓ, μ, а, r, α₁, α₂. геометриялық өлшемдерді суреттейді

Вектор Н нүктесінен р ағымдағы элементтен бастап (4.14) теңдеу арқылы анықталады

  б) Тогы бар дөңгелек кезекті магниттік өріс.

4.8-суретінде тогы бар дөңгелек өткізгіш көрсетілген. Р нүктесінде
магнит өрісінің беріктігі векторы ось бойындағы компоненттерден х, сондықтан
y осі бойындағы компоненттер шегеріліп, нөлге дейін қосылады.

4.8 Магниттік өріс үлгісін жасаудың графикалық әдісі

 

Магниттік медианың күрделі конфигурациясымен, магнит өрісінің аналитикалық есептелуі мүмкін емес және оның параметрлері графикалық түрде өрістің суретімен анықталады. Құрылыстың негізі ауадағы магниттік индукция сызықтары паримагнетикалы медианың бетіне қалыпты болып табылады, ол әлеуетті әлеуетті беттер сияқты қарастырылуы мүмкін.Өрістің суретін салу үшін келесі шарттар орындалуы керек:- Магнит өрісінің беріктігінің V сызықтары және тең магниттік әлеует  φ_м сызығы барлық жерде оң бұрышпен қиылысу керек;- Фармагмагнитофонның беттерін тең магниттік әлеуеттің беттерімен қарастыру керек және магниттік күштердің күштері оларға дұрыс бұрыштарда;- Қуат магниттік сызықтары мен эквипотенциалды сызықтармен құрылған тор торлары олардың тығыздығы жеткілікті болғанда бір-біріне ұқсас болуы керек.

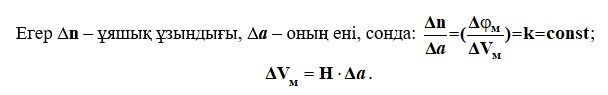
Өрістін суретін пайдалана отырып,түсінетініміз: магниттік қарсылық,

R_м (); магнитті өткізгіш, G_м (); магниттік ағын, Ф (Вб); магниттік индукция, В (Тл); магнитталған күш, F (А), ауа ағыны арқылы өткізетін қажетті магниттік өрес және т.б.

а) электр машинасының роторы мен стататор арасындағы ауа айырмашылығындағы магнит өрісінің құрылымының графикалық құрылысы.

4.9-суретте статор мен электр машинасының роторы арасындағы ауаның арасындағы айырмашылық өріс үлгісі көрсетілген. 4.9. А-А желісіндегі магниттік индукция белгілі және В_отең

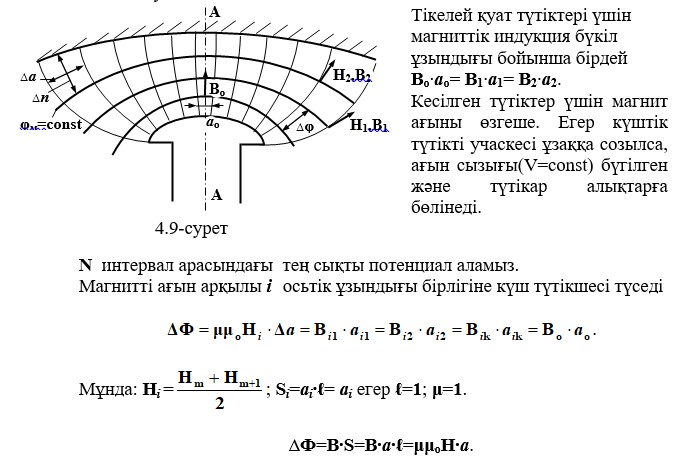
а_о орталық қуат түтігінің ені белгілі, мұнда В_о берілген (4.9-сурет). онда қуат түтігінің кез келген басқа жасушасындағы магниттік индукция қарапайым сызықтық қатынаспен анықталады (k -интервалында, жалпы N интервалында):

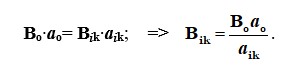
Егер қуат түтікшесінде N аралығы болса, онда МДС ауаның аралықтың бүкіл ұзындығы бойынша

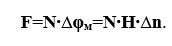
Магнит ағыны қуат түтіктерінің саны бар М-ге тең

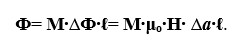
Магниттік қарсылық

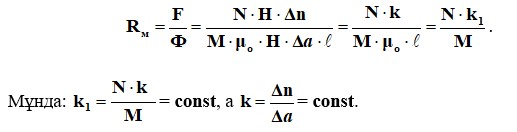
4.9 Электростатикалық өріс суретін салудың графикалық әдісі 

Егер зарядталған корпустың көлденең қимасының пішіні және олардың орналасуы күрделі болса, электростатикалық өріс суретін салудың графикалық әдісі қолданылады.

Құрылыс кезінде келесі шарттарды сақтау қажет:

- E электростатикалық өрістің беріктік желілері және тең әлеуеті φ сызықтары оң жақ бұрыштарда қиылысу керек;

- электростатикалық өрістің қарқындылығы желілердің көлденең қимасын шектейтін контурға қалыпты;

- E сызықтарымен және сызықтармен құрастырылған торлы жасушалар жеткілікті тығыздығы бар бір-біріне ұқсас болуы керек.Демек, өріс тең ағындық түтіктерге (ΔV = const) бөлінген және көршілес эквипотенциалды сызықтар арасындағы ықтимал айырмашылық бірдей болуы керек (Δφ = const). Кез келген нүктеде өріс күші

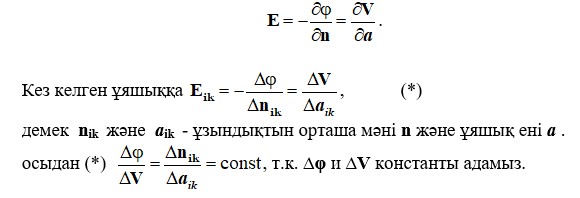
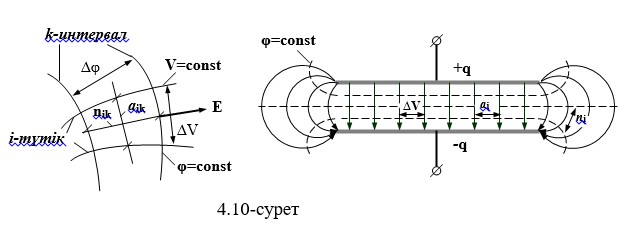
Әдетте өріс үлгісін салу екі кезеңде жүзеге асырылады. Алдымен сурет жоғарыда айтылған алғашқы екі шартты сақтай отырып, өрістің шамамен бейнесі, содан кейін үшінші жағдайға сәйкес түзетулер жасаңыз.  4.10-суретте жазық конденсатордың өріс үлгісі көрсетілген. Шеттерінде платина қисаюының өзгеруіне байланысты шиеленіс күшейіп, күштер желісін қалыңдайды.

U = Δφ ∙ N конденсатордың кернеуі, мұндағы N - электродтар (плиталар) арасындағы қуат түтігі бойымен аралықтардың саны. 4.10-суретте, N = 4

Пластина заряды

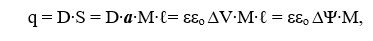
S=a∙M∙ℓ - пластина ауданы; a∙M – ені, ℓ - пластина ұзындығы суретке перпендикуляр бағытта ; М – интервал мөлшері күштік сызыққа перпендикуляр бағытта (күштік түтік); d –пластина арасындағы қашықтық.

Егер ℓ >> d, онда пластина арасындағы тегіс параллель мен конденсатор сыйымдылығы