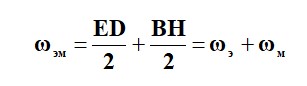1.1 Анықтамалар. Электрлік және магниттік өріс арасындағы байланысты анықтайтын теңдеулер

 

Электромагниттік өріс – бұл материяның ерекше түрі. Барлық зарядталған дене электромагниттік өріспен қоршалған және онымен бір тұтас болып келеді. Бұл денелер электрлі зарядталған бөліктерден бөлек 3·10⁸ м/с жылдамдықпен тіршілік етуі мүмкін. Электромагниттік өріс, мысалы, фотон, өзінің энергиясын тарату арқылы екі материялық бөлікке бөлінеді: электрон және позитрон.

Электромагниттік өріс энергияны тасымалдаушылар болып табылады. Олар белгілі салмаққа ие, дегенмен өте аз мөлшердегі салмақ болғандықтан қарапайым әдіспен анықталмайды.

Табиғатта біртұтас электромагниттік өріс қалыптасқан. Оны екі бөлікке, электрлік және магниттік өріске бөлу физикалық және техникалық мәселелерге байланысты туады, ол құбылыстарды макроскопиялық түрде қарастыруға байланысты болды.

Заряд қозғалысы кезінде байқалған өріс магниттік қүштің кері қайтаруы кезінде, дайындалған заряд қозғалысы кезінде байқалады. Бірақ, бақылаушы зарядпен бірге қозғалса, онда тек электрлік өріс байқалады. Берілген шарт бақылаушының нәтижесіне әсер етеді.

Электрлік және магниттік өріс теңдеулерінің байланысын қарастырамыз. Магниттік өріс және электрлік токтың арасындағы байланыстолық токтың заңымен анықталады

Магнит өрісінің беріктігі векторының сызықтық интегралы кез-келген тұйық цикл үстінен осы контур бойымен қалыпты бағытта шектелген бет арқылы өтетін жалпы токпен тең болады

Ішкі беті арқылы өтетін S қисық сызықпен шектелген l бетіндегі интегралға тең.  - ағымдағы тығыздық векторы.

ЭТН курсында токтың үш түріне ажыратылады:

- Өткізгіштегі заряд тасымалдаушылардың реттелген қозғалысы өткізгіш ток деп аталады. Электр өткізгіштің ток тығыздығының векторы электр өрісінің күшіне сәйкес келеді 

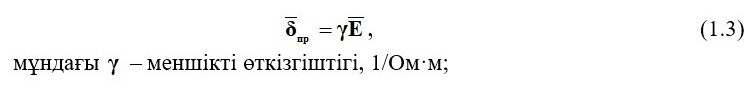
Е – электр өрісінің беріктік кернеуінің векторы, В/м.

 

- Зарядталмайтын ортада немесе вакуумдағы заряд тасымалдаушылардың реттелген қозғалысы трансфер тогы деп аталады. Осы ток тығыздығының векторы заряд тығыздығының көлеміне және олардың қозғалыс жылдамдығына пропорционалды

- Диэлектриктерде поляризациядан туындаған бұрылыс тогы байқалады, ток тығыздығы векторы электрлік ығысу векторының өзгеру жылдамдығына пропорционал (электрлік индукция)

Егер бұл теңдеуде (1.1) ∑I   токтың үш түрін қарастырылатын болса,онда бұл Максвеллдің интегральді түрдегі бірінші теңдеуі

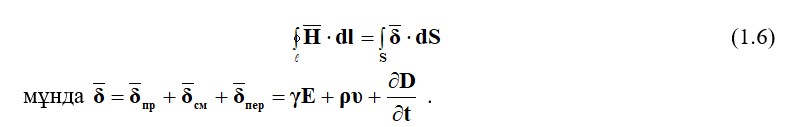
Физикалық тұрғыдан бұл теңдеу, мгниттік өріс тек  ток өткізгішінен емес,сонымен қатар электрлік өріс уақытымен де жасалатынын түсіндіреді.

Электромагниттік индукцияның заңына сәйкес, Фараданың тұжырымдамасы, магнит ағыны тізбекте, катушкаларда немесе өткізгіште өзгерген кезде, шамасы минус белгісі бар ағынның өзгеру жылдамдығына тең ЭҚК. Бұл Максвелл түсіндірмесі. Ол осы заңды кез-келген ортаға қатысты жалпылап жариялады

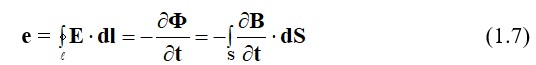
(1.7) өрнек интегрральді түрдегі Максвеллдің екінші теңдеуі.

Оның физикалық мағынасы мынада, электр өрісі тек зарядталумен ғана емес, сонымен қатар өзгеретін магнит өрісі арқылы да құрылады. Магнит ағыны арасындағы байланыс Ф, магнит индукциясы В, беткі аудан S және магнит өрісінің қарқындылығы Н келесідей

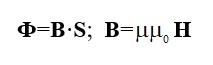
1.2 Дифференциальді түрдегі Максвелл теңдеуі

 

Есептерді шешу барысында электрлік өрістің параметрлерін анықтау нүктенің орналасуына байланысты қарастырылады (мысалы, E, D, H, B, φ, ε, ε₀, μ₀).

Бұл жағдайда Максвелл теңдеулерінің ажырамас формасы әрдайым қанағаттандырмайды және дифференциалды түрде жазылуы керек. Математикадан белгілі болған  

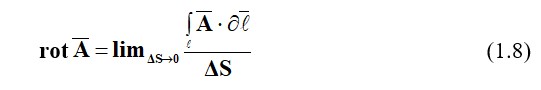
Кейбір вектордың роторы А вектордың айналымының қатынасы лимитіне тең А ауданға ΔS интеграцияның контуры ұмтылыспен шектелген .

rot вектор проекциясы бар А бағыты нормал бетінде S қарастырылатын нүкте. Сондықтан rot максималды болады, егер вектор бағыты бағыт нормасымен сәйкес келсе.

Қалыпты бағыт rot контурды оң жаққа бағыттаудың бағытына байланысты. Сәйкесінше (1.8) Максвелл теңдеуін дифференциальді түрде жазамыз

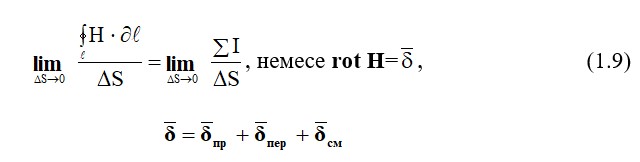
(1.9) өрнек – Максвелл теңдеуінің дифференциальді түріндегі бірінші теңдеуі.

Ұқсастығы бойынша

(1.10) өрнек – Максвелл теңдеуінің дифференциальді түріндегі бекінші теңдеуі.

 

1.3 Тіктөртбұрышты координат жүйесіндегі Максвелл теңдеуінің дифференциальді түрі

 

(1.9) және (1.10) теңдеулері таңдалған координат жүйелеріне тәуелді емес. Бірақ берілген өрнек векторлары Е немесе Н әртүрлі координат жүйелерінде ажыратылады. Тіктөртбұрышты координат жүйесінде

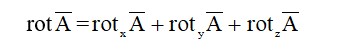
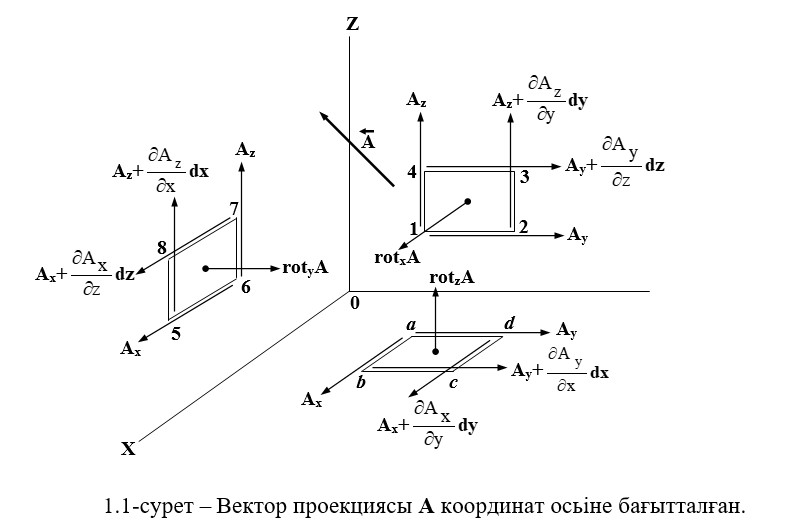
Бұл жерде құраушы проекциялар бар rot A мына ось бойынша x, y, z. rot A бойынша өрнекті анықтаймыз. Ол үшін ауданды анықтау керек ds (тіктөртбұрышты контур) 12341 жазықтыққа параллель жазықтықта YOZ координат жүйесінде XYZ (сурет.1.1)

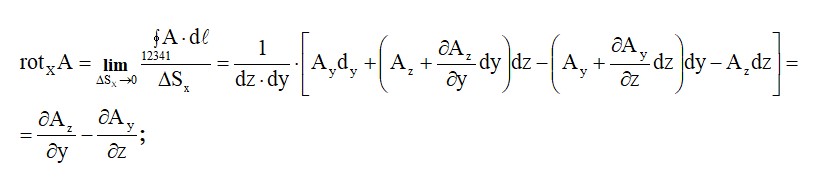
Ұқсастығы бойынша басқа проекциялар үшін  мынаны аламыз:

(1.11) теңдеулер жүйесін үшінші рет бойынша анықтап алуға болады

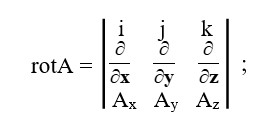
Сәйкесінше (1.11) теңдеуді жазып алып (1.9) және (1.10), Максвеллдің бірінші (1.12) және екінші теңдеуін (1.13) декарттық координатадан алуға болады.

 

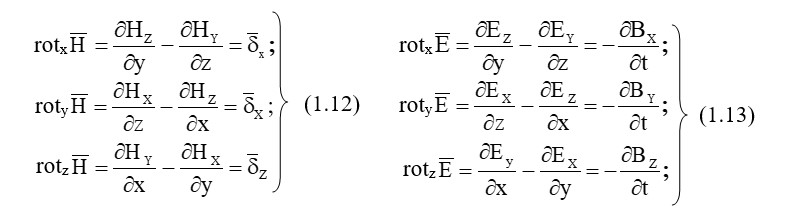
1.4 Дифференциальді түрдегі Гаусс теоремасы және Максвелл постулаты

 

Теорема бойынша: электр өрісінің беріктігі векторының ағыны Е жабық беті арқылы S біртекті және изотропты ортада беті шектелген кеңістіктің көлеміне қойылған электрлік зарядтың қатынасына тең S, абсолютті диэлектрик өтімділігімен εε₀, т.б:

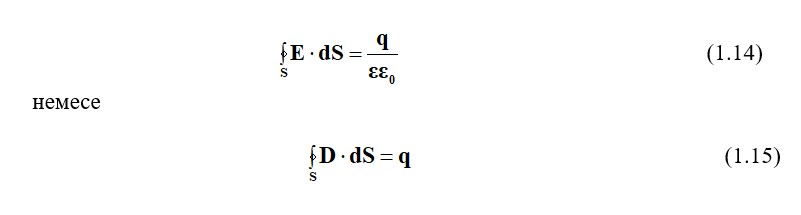
Бұл интегралдар – электрлік зарядтың сандық өлшемі, жабық бетімен шектелген көлемде S. Тарату заңын электрлік зарядтың ішкі көлемін Гаусс теоремасы арқыды дифференциальді түрде анықтауға болады.

Мысалға аз көлемде электр заряды бар екенін анықтау керек болса, осы нүкте арқылы А және оның тығыздығына байланысты болса ρ.

Онда бөліктеп (1.14) ΔV, ұмтылысын алу арқылы , мынаны аламыз

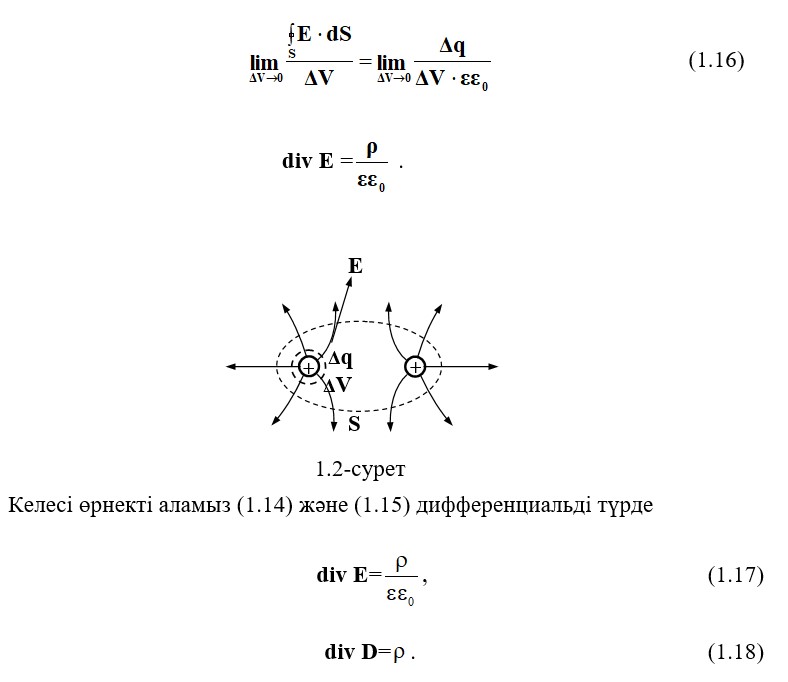
(1.17) –Гаусс теоремасы,  (1.18) – Максвелл постулаты дифференциальді түрде.

Постулаттың физикалық мағынасы– электр қозғалтқышының вектор ағыны D жабық беті арқылы S кез-келген ортада массаның тығыздығына тең ρ жабық бетімен шектелген көлемде бос электр заряды.

Дивергенция (алшақтық) векторы А–ағынның шегі бар беткі көлем векторы қатынасына ΔV, жабық жердің ішіне S нөлге ұмтылғанда ΔV.

Оң заряд q₊ ретінде қарастыруға болады көзі күш сызықтарының электр өрісінің Е, осының жанында сызықтар басталады.Теріс заряд q_-ағын ретінде қарастырылады, оның жанында күш сызықтары қарқынмен аяқталады. Сондықтан,кейбір көлемде ΔV электр зарядының көлемдік тығыздығы ρ нөлге тең емес, онда куш сызықтары тұйық бет арқылы ортаға осы вектор арқылы таралады divЕ ≠ 0.

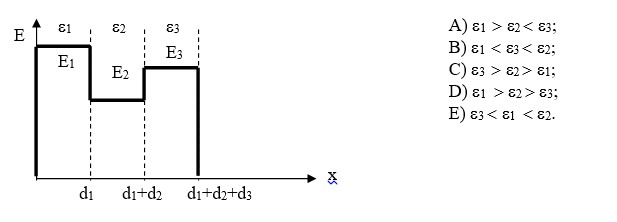
Егер көлемде заряд жок болса, онда күш сызықтары Е көлемде электр өрісі сәйкес келмесе және таралмаса, тек соқтығысса ,онда суреттегідей жағдай орын алады 1.3-сурет

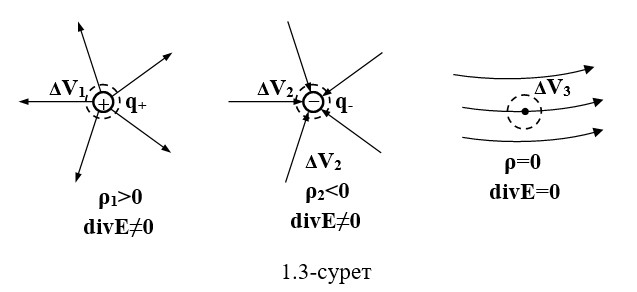
Арнайы үш көлем үшін келесідей мағына аламыз

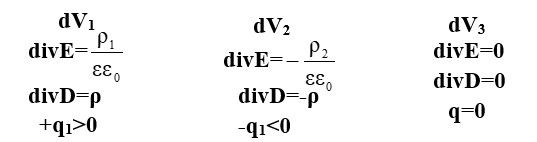
Өрнекте (1.16) және (1.17) оператор Гамильтонды қолдана отырып мынаны көрсетуге болады

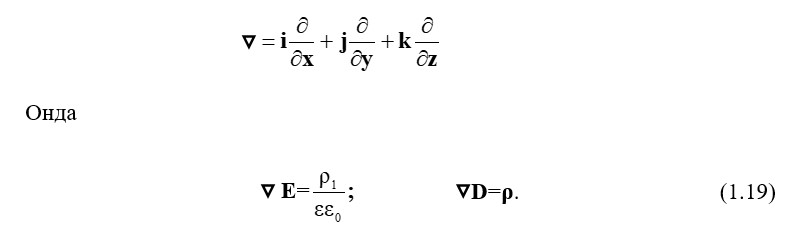
Оператор арқылы біз тиісті векторлардың (бірліктердің) көбейтілген үш координаталық осіне қатысты жартылай туындылар сомасын аламыз. Ресми түрде бұл вектор және скаляр және векторлық функцияларға қолданылады.

 

1.5 Тіктөртбұрышты координат жүйесіндегі Гаусс теоремасы және Максвелл постулаты

 

Мұнда, 1.3 бөлімінде айтылғандай, кейбір компоненттері арқылы А векторының өрнегі әр түрлі координат жүйелерінде әртүрлі болады. 1.4-суретте тікбұрышты координат жүйесі үшін түсіндірме сызба берілген.                                                                                  

 А вектордың тік бұрышты параллелепипедтер бетіндегі ағыны оның көлемін қалыптастыратын беттерден шығып тұрады. A векторының ағыны параллелепипед көлемін шектейтін жабық бет арқылы өтіп, оның векторының ағындарының алгебралық санына тең болады. Көлемнен шығатын ағындар «+» белгісіне ие, ол «-» белгісін береді.

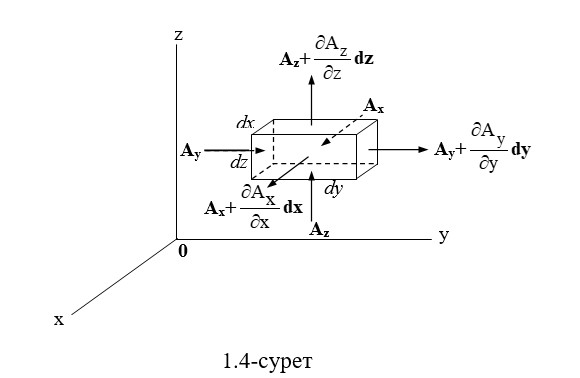
1.4-суретте вектордың беткі шегінің орташа мәндері көрсетілген.

Беткі аудан dS және параллелепипед көлемі dVсәйкесінше тең

 

dS = 2dx·dy + 2dy·dz + 2dz·dx;  dV = dx·dy·dz.

 

Вектор ағыны А тұйық бет арқылы тең

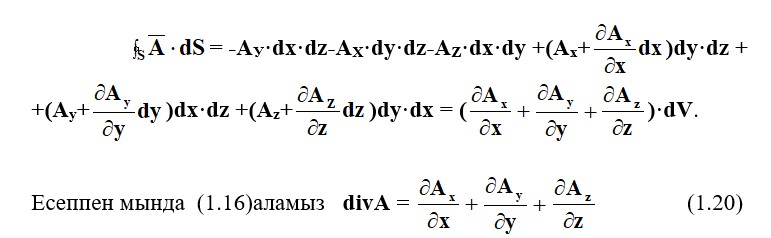
Гаусса теоремасы дифференциаьді түрде

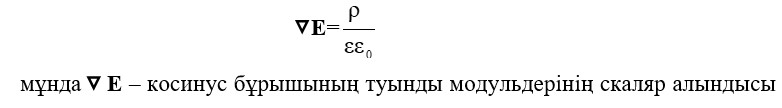
Декарттық координата жүйесінде Гаусс теоремасы

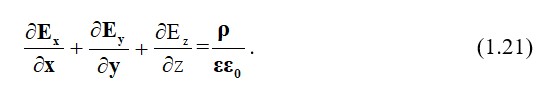
Декарттық координатада және дифференциальді түрдегі Максвелл постулаты

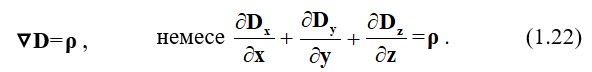
1.6 Дифференциальді түрдегі электр тогының үздіксіздік принципінің өрнектелуі

 

Табиғатта магниттік массалар жоқ, олар магниттік индукция желісінің көздері болып табылады, электрлік зарядтар сияқты, электр өрісінің электр желілерін тудырады. Магнит өрісі электр тоғымен ғана пайда болады. Күштің магниттік сызықтары (магниттік индукция сызығы) өткізгішті токпен, әрқашан жабық және үздіксіз қоршайды.

Магнит ағынының үздіксіздігі принципі магниттік индукция сызықтары еш жерде басталмаса немесе аяқталса, онда олар үздіксіз болып қалады. Сондықтан кез-келген магниттік өріске магнит өрісі әрдайым нөлге тең

Магниттік ағынның және теңдіктің үздіксіздігінің принципін математикалық тұжырымдау (1.21) интегралды түрде жазылған.

Дифференциалды түрде (1.21) магниттік ағынның үздіксіздігі принципі бар

Электр тізбектерін есептеу тәжірибесінен электр тогының тек тұйық тізбектің көмегімен ағып жатқаны белгілі, сондықтан электр тогының сызықтары кез-келген жерде үзілмейді, олар әрқашан жабық.

Сыртқы қалыпты бағытта кез-келген тұйық бет арқылы өтетін толық ток нөлге тең.

Интелгральді түрде ол былай жазылады

Дифференциальді түрде ол былай жазылады

Толық ток барлық үш түрлі токты қамтиды , т.б.

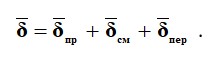
Егер δ орнына (1.24) rotH=δ ертерек алынған мағынасын алсақ,  онда мынаны аламыз

Н векторы үшін оның нөлге тең екенін аламыз.

1.7 Остроград және Стокс теоремасы

 

Остроград-Гаусс  теоремасы көлемнен беттік интегралға өтуге мүмкіндік береді.

Теорема: вектордың А-ның дивергенттің көлемді интегралы осы көлемді шектейтін жабық бет арқылы А векторының ағынымен алмастырылуы мүмкін

div A – бұл вектордың ағынының қатынасы А шектік көлемнің беті арқылы dV.

Көлемді интегралды құрастырған кезде,іргелес көлемдегі беттердің беттерінде ағымдар шамаға тең болады, қарсы белгілерге ие, сондықтан олардың сомасы нөлге тең.

Электрлік жылжыту векторының D ағыны жабық беті арқылы жабық бетпен шектелген көлемде қамтылған еркін электр зарядына тең.

Стокса теоремасы беттік интегралдан сызықтық интегралға өтуге мүмкіндік береді және түсіндіріледі: вектор ағымы rotA жабық беті арқылы өнімнің (айналымның) сомасына тең вектор А контурдың барлық жағында, шектік беті S.

1.8 Электромагниттік өріс теңдеуінің толық жүйесі

 

Шын мәнінде электромагниттік өріс, заттарда өте күрт өзгереді кеңістікте нүктеден нүктеге дейін арасындағы қарапайым бөлшектермен заттар және уақыт аралығында, салдарынан үлкен жылдамдықтың элементар бөлшектеріне әсер етеді. Алайда, бұл өзгерістер микроскопиялық сипаты бойынша.

Оқу барысында электромагниттік процестерді біз ескермеуіміздің себебі олар біртекті емес, олардың орташа мәндерін кеңістіктегі және уақыт бірлігінде пайдаланатын боламыз.

Сондықтан электромагниттік өріс үшін  теңдеулер жүйесінің толық түрі кез келген изотропты ортада бар

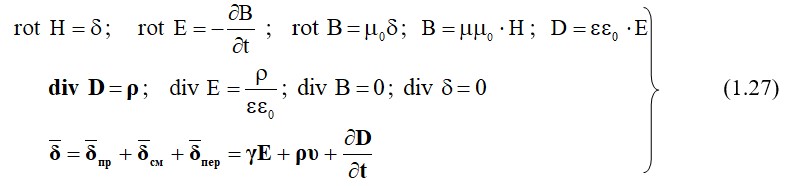
Осы өткізгіш және ток өткізбейтін ортада кейбір құрамдас теңдеулер (1.27) болады соны ескеру керек.

Электромагниттік өрістің көлемдік энергиясы