3.1. Шкалы и варианты оценок

Для оценивания спортивных результатов часто прибегают к специальным таблицам очков. Цель таких таблиц – преобразование показанного спортивного результата (выраженного в объективных мерах) в условные очки.

Закон преобразования спортивных результатов в очки называется шкалой оценок. Шкала может быть задана в виде математического выражения, таблицы или графика.

Различают 4 основных типа шкал, используемых в спорте и физическом воспитании.

Пропорциональные шкалы предполагают начисление одинакового числа очков за равный прирост результатов (например, за каждые 0,1 с улучшения результата в беге на 100 м начисляется 20 очков). Такие шкалы используются в современном пятиборье, конькобежном спорте, гонках на лыжах, лыжном двоеборье, биатлоне и других видах спорта.

Регрессирующие шкалы предполагают начисление (за один и тот же прирост результата по мере возрастания спортивных достижений) всё меньшее число очков (например, за улучшение результата в беге на 100 м с 15,0 до 14,9 с добавляют 20 очков, а за 0,1 с в диапазоне 10,0–9,9 с – только 15 очков).

Прогрессирующие шкалы. Здесь чем выше спортивный результат, тем большей прибавкой очков оценивается его улучшение (например, за уменьшение времени в беге в диапазоне 15,0–14,9 с, добавляют 10 очков, а в диапазоне 10,0–9,9 с – 100 очков). Прогрессирующие шкалы применяются в плавании, в отдельных видах лёгкой атлетики, тяжёлой атлетике.

Сигмовидные (или S-образные) шкалы редко используются в спорте, но широко применяются при оценке физической подготовленности (например, так выглядит шкала стандартов физической подготовленности населения США). В этих шкалах улучшение результатов в зоне очень низких и очень высоких достижений поощряется скупо; больше всего очков приносит прирост результатов в средней зоне достижений.

Каждая из этих шкал имеет как свои достоинства, так и недостатки. Устранить последние и усилить первые можно, правильно применяя ту или иную шкалу.

Оценка как универсальный измеритель спортивных результатов может быть эффективной, если она справедлива и с пользой применяется в практике. Это зависит от критериев, на основе которых оцениваются результаты.

Целесообразно использование следующих критериев:

1. равенство временных интервалов, необходимых для достижения результатов, соответствующих одинаковым разрядам в разных видах спорта. Естественно, что это возможно лишь в том случае, если содержание и организация тренировочного процесса в этих видах спорта не будет резко отличаться;
2. равенство объёмов нагрузок, которые необходимо выполнить для достижения одинаковых квалификационных норм в разных видах спорта;
3. равенство мировых рекордов в разных видах спорта;
4. равные соотношения между числом спортсменов, выполнивших разрядные нормы в разных видах спорта.

В практике для оценок результатов тестирования используются разные шкалы оценок.

Стандартная шкала. В её основе лежит пропорциональная шкала, а своё название она получила потому, что масштабом в ней служит стандартное (среднеквадратическое) отклонение. Наиболее распространена Т-шкала. При её использовании средний результат приравнивается к 50 очкам, а вся формула выглядит следующим образом

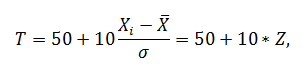
где Т – оценка результата в тесте; 50 – средний результат, выраженный в баллах; 10 – коэффициент приведения; X_i – показанный результат; X̅ – средний результат; σ – стандартное отклонение; Z – нормированный показатель (отношение разности частного центрального отклонения к групповому стандартному отклонению).

Пример. Если средняя величина в прыжках в длину с места равнялась 224 см, а стандартное отклонение – 20 см, то за результат 222 см начисляется 49 очков, а за 266 см – 71 очко (проверьте правильность этих вычислений).

В практике используются и другие стандартные шкалы.

Перцентильная шкала. В основе этой шкалы лежит следующая операция: каждый спортсмен из группы получает за свой результат (в соревнованиях или в тесте) столько очков, сколько процентов спортсменов он опередил. Таким образом, оценка победителя составляет – 100 очков, оценка последнего – 0 очков. Перцентильная шкала наиболее пригодна для оценки результатов больших групп спортсменов. В таких группах статистическое распределение результатов нормальное (или почти нормальное). Это значит, что очень высокие и очень низкие результаты показывают единицы из группы, а средние – большинство. Главное достоинство шкалы – простота, здесь не нужны формулы, а единственное, что нужно вычислить, – какое количество результатов спортсменов укладывается в один перцентиль (или сколько перцентилей приходится на одного человека). Перцентиль – это интервал шкалы; при 100 спортсменах, в одном перцентиле – один результат; при 50 – один результат укладывается в два перцентиля (т. е. если спортсмен обошёл 30 человек, он получает 60 очков). Простота обработки результатов и наглядность перцентильной шкалы обусловили её широкое применение в практике. Например, она часто используется при оценке физического развития.

Шкалы выбранных точек. При разработке таблиц по видам спорта не всегда удаётся получить статистические распределения результатов теста. Тогда поступают следующим образом: берут какой-нибудь высокий спортивный результат (например, мировой рекорд или 20-й результат в истории данного вида спорта) и приравнивают его, скажем, к 1000 или 1200 очкам. Затем на основе результатов массовых испытаний определяют среднее достижение группы слабо подготовленных лиц и приравнивают его, скажем, к 100 очкам. После этого, если используется пропорциональная шкала, остаётся выполнить лишь арифметические вычисления – ведь две точки однозначно определяют прямую линию. Построенная таким образом шкала называется шкалой выбранных точек.

Последующие шаги для построения таблиц по видам спорта – выбор шкалы и установление межклассовых интервалов (научно пока не обоснованы), здесь допускается определённый субъективизм, основанный на личном мнении специалистов.

Параметрические шкалы. В видах спорта циклического характера и в тяжёлой атлетике результаты зависят от таких параметров, как длина дистанции и масса спортсмена. Эти зависимости называют параметрическими.

Можно найти параметрические зависимости, которые являются геометрическим местом точек эквивалентных достижений. Шкалы, построенные на основе этих зависимостей, называются параметрическими и относятся к числу наиболее точных.

Шкала ГЦОЛИФКа (разработана в Государственном центральном Ордена Ленина институте физической культуры, ныне РГУФК). Рассмотренные выше шкалы используются для оценки результатов группы спортсменов, и цель их применения заключается в определении меж индивидуальных различий (в баллах).

В практике спорта тренеры постоянно сталкиваются с ещё одной проблемой – необходимостью оценки результатов периодического тестирования одного и того же спортсмена в разные периоды цикла или этапа подготовки. Для этой цели предложена шкала ГЦОЛИФКа, выраженная в формуле

Смысл такого подхода заключается в том, что результат теста рассматривается не как отвлечённая величина, а во взаимосвязи с лучшим и худшим результатами, показанными спортсменом (в разное время) в данном тесте. Как видно из формулы, лучший результат всегда оценивается в 100 очков, худший – в 0 очков. Эту шкалу целесообразно применять для оценки вариативных показателей физической подготовленности.

Оценка комплекса тестов. Существует три основных варианта оценки результатов тестирования спортсменов по комплексу тестов.

Первый вариант оценки заключается в выведении обобщённой оценки, которая информативно характеризует подготовленность спортсмена, определяющая результат в соревнованиях. Это позволяет использовать её для прогноза: рассчитывается уравнение регрессии, решив которое, можно предсказать результат в соревновании по сумме баллов за тестирование. Однако просто суммировать результаты конкретного спортсмена по всем тестам было бы неправильно, так как сами тесты неравнозначны. Например, из двух тестов (времени реагирования на сигнал и времени удержания максимальной скорости бега) второй более важен для спринтера, чем первый. Эту важность (весомость) теста можно учитывать тремя способами:

• даётся экспертная оценка. В этом случае специалисты договариваются, что одному из тестов приписывается коэффициент 2. И тогда очки, начисленные по этому тесту, вначале удваиваются, а затем суммируются с очками за другой тест;
• коэффициент устанавливается каждому тесту на основе факторного анализа. Он, как известно, позволяет выделить показатели с большим или меньшим факторным весом;
• количественной мерой весомости теста может быть значение коэффициента корреляции, рассчитанного между его результатом и достижением в соревнованиях.

Во всех этих случаях полученные оценки называются «взвешенными».

Второй вариант оценки результатов комплексного контроля заключается в построении «профиля» спортсмена – графическая форма представления результатов тестирования. Линии графиков наглядно отражают сильные и слабые стороны подготовленности спортсменов.

Третий вариант оценки – интегральный, выполняется в два этапа. Сначала устраняется размерность, т. е. осуществляется приведение различных показателей (тестирования, измерения) к единому виду. Для этого рассчитывается средняя арифметическая величина (X̅) какого-либо признака, затем вычисляется индекс измеряемого показателя для каждого спортсмена по формуле

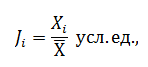    (7)

ГдеJ_i – индекс измеряемого показателя у конкретного спортсмена; x_i – абсо- лютное значение измеряемого показателя у конкретного спортсмена; X̅– средняя арифметическая для исследуемого признака.

После преобразования, уничтожающего размерность отдельных признаков (результаты в тестах), для каждого в отдельности спортсмена (или разных групп) вычисляется интегральная оценка по формуле

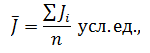    (8)

где J̅ – средний индекс по всем признакам (результаты в тестах) для отдельного спортсмена (или группы);J_i – индекс измеряемого показателя у конкретного спортсмена; n – количество измеренных показателей в тестах.

Средний индекс по всем признаком служит интегральной оценкой результативности в тестах. В случаях, когда встречается разная модальность (знак + или – ) того или иного признака в тесте, то определение его результативности осуществляется вычислением простой разности между индексом измеряемого показателя (J_i) у конкретного спортсмена и единицей (1). Например, чем меньше время пробегания дистанции на 60 м, тем лучше результат (1 – J_i).

Основными задачами оценивания являются:

• сопоставление разных достижений в одном и том же задании;
• сопоставление достижений в разных заданиях;
• определение нормы.

3.2 Разновидности норм сравнения

Нормой в спортивной метрологии называется граничная величина результата, служащая основой для отнесения спортсмена к одной из классификационных групп. Существует три основных вида норм: сопоставительные, индивидуальные, должные.

Сопоставительные нормы имеют в своей основе сравнение людей, принадлежащих к одной и той же совокупности. Процедура определения сопоставительных норм такова:

1. выбирается совокупность людей (например, студенты вузов Павлодарской области);
2. определяются их достижения в комплексе тестов;;
3. определяются средние величины (X̅) и стандартные отклонения (σ);
4. значение X̅ ± 0,5σ принимается за среднюю норму, а остальные градации (ниже средней – выше средней, низкая – высокая, очень низкая – очень высокая) – в зависимости от избранного коэффициента при данной σ.

По аналогии, например, можно осуществлять «разбивку» людей на подгруппы по степени устойчивости (высокой, средней, низкой) или реактивности (гипер-, нормо-, гипореактивные) к гипоксии, холоду и т. п. Эти нормы характеризуют лишь сравнительные успехи испытуемых в данной совокупности, но ничего не говорят о совокупности в целом (или в среднем). Поэтому сопоставительные нормы должны сравниваться с данными, полученными на других совокупностях, и использоваться в сочетании с индивидуальными и должными нормами. Индивидуальные нормы основаны на сравнении показателей одного и того же спортсмена в разных состояниях. Эти нормы имеют исключительно важное значение для индивидуализации тренировки во всех видах спорта. Необходимость их определения возникла вследствие существенных различий в структуре тренированности спортсменов.

Градация индивидуальных норм устанавливается с помощью тех же статистических процедур. За среднюю норму здесь можно принимать показатели тестов, соответствующие среднему результату в соревновательном упражнении.

Индивидуальные нормы широко используются в текущем контроле. Например, во многих видах спорта нет зависимости между массой тела спортсменов и спортивным результатом. У каждого спортсмена есть индивидуально оптимальная масса тела, соответствующая состоянию спортивной формы. Эту норму можно контролировать на разных этапах спортивной подготовки. Должные нормы основаны на анализе того, что должен уметь человек, чтобы успешно справляться с задачами, которые перед ним ставит жизнь. Примером этому могут служить нормативы отдельных комплексов по физической подготовке, должные величины жизненной ёмкости лёгких, основного обмена, массы и длины тела и т. п.

В спортивной практике должные нормы устанавливаются следующим образом:

1. определяются информативные показатели подготовленности спортсмена;
2. измеряются результаты в соревновательном упражнении и соответствующие им достижения в тестах;

рассчитывается уравнение регрессии типа

y=a+b*x   (9)

где у – прогнозируемый результат в соревновательном упражнении; a – свободный член; b – коэффициент регрессии; x – результат, который должен спортсмен показать в тесте на данном этапе подготовки.

Должные результаты в тесте и являются должной нормой. Её необходимо достичь, и только тогда можно будет показать запланированный в соревновании результат.

В основе сопоставительных, индивидуальных и должных норм лежит сравнение результатов одного спортсмена с результатами других спортсменов, показателей одного и того же спортсмена в разные периоды и в разных состояниях, имеющихся данных с должными величинами.

В практике физического воспитания наибольшее распространение получили возрастные нормы. Типичным примером являются нормы комплексной программы «Президентские тесты».

Большинство из этих норм составлялись традиционным способом: результаты тестирования в различных возрастных группах обрабатывались с помощью стандартной шкалы, и на этой основе определялись нормы. В таком, методическом подходе есть один существенный недостаток – ориентация на паспортный возраст человека не учитывает существенного влияния на любые показатели биологического возраста и размеров тела.

Понятно, что при использовании традиционных норм (таблиц) для изучения, например, физической подготовленности детей определённого возраста часть параметров может быть меньше или больше нормативных значений. В этом случае определяется средняя арифметическая весомостей по всем тестам, комплексно отражающая двигательный возраст ребёнка.

Известно большое разнообразие норм, которые предназначены для оценки физического развития, физической подготовленности, функционального состояния организма и др. Однако существует их специфичность, связанная с множеством факторов – возраст, пол, этническая принадлежность, экология, вид спорта, уровень спортивной подготовленности и мн. др. Эти факторы определяют пригодность (релевантность) тех или иных норм только для той совокупности, для которой они разработаны.

Репрезентативность норм отражает их пригодность для оценки всех людей из генеральной совокупности. Репрезентативными могут быть только нормы, полученные на типичном материале.

Одна из важных характеристик норм – их современность. Известно, что результаты в соревновательных упражнениях и тестах постоянно растут, поэтому пользоваться разработанными давно нормами не рекомендуется. Некоторые нормы, установленные много лет назад, в большинстве своём не приемлемы для настоящего времени, хотя в своё время они отражали действительную ситуацию.