Модуль. Түзу сызық
Модуль. Түзу сызық
Түзу сызық – бұл ұзындығы бар бір өлшемдік геометриялық бейне, көптеген барлық қозғалмалы нүктелердің жиыны. Түзу сызықтың кесіндісі екі нүктемен анықталады. Екі нүктенің проекциясын түзудің проекциясымен анықтайды. Жалпы жағдайда түзудің проекциясы әрқашанда түзудің өзінен кем болады.
Түзудің проекциясы бойынша оның проекция жазықтықтарына көлбеу бұрышын анықтауға болмайды. Жалпы жағдайда түзу сызықты проекциялау үшін оның екі нүктесін проекциялау керек және нүктелердің табылған проекцияларын өзара қосу қажет. Кеңістіктегі түзу еркін орналасуы мүмкін. Түзудің проекциясын салу үшін нүктені проекциялауға қатысты барлық ережелерді қолдануға болады.
2.1 Блок. Жалпы және дербес жағдайдағы түзулер
Мысал



2.1 сурет – АВ денгейлік түзулердің проекциялары
а) горизонталь түзуі: A2B2 || π 1; A1B1 – АВ кесіндісінің нақты өлшемі; β – π 2 жазықтығына көлбеу бұрышы; б) фронталь түзуі: A1B1|| π 2; A2B2 – АВ кесіндісінің нақты өлшемі; α– π 1 жазықтығына көлбеу бұрышы; в) профиль түзуі: A2B2 || π 3; A3B3 – АВ кесіндісінің нақты өлшемі; β – π 2 жазықтығына көлбеу бұрышы
Түзулер жалпы және дербес жағдайдағы деп бөлінеді. Проекция жазықтықтарына параллель емес және перпендикуляр емес түзулерді жалпы жағдайдағы түзулер деп атайды.
Жалпы жағдайдағы түзудің бір де бір проекциясы оның нақты өлшемін көрсетпейді, сондай-ақ проекция жазықтығының көлбеу бұрышы да нақты өлшемін көрсетпейді. Мұндай түзудің кез келген проекциясы түзудің өзінен кем болады. Сонымен, жалпы жағдайдағы түзу үшін мына тұжырым ақиқат: нақты өлшемі оның кез келген проекциясынан артық немесе тең. Проекция жазықтықтарына параллель немесе перпендикуляр жатқан түзулерді дербес жағдайдағы түзулер деп атайды. Дербес жағдайдағы түзулер денгейлік және проекциялаушы түзулерге бөлінеді. Түзулер проекция жазықтығына параллель орналасса оларды денгейлік түзулер деп атайды және келесідей белгілейді: h горизонталь, f фронталь және р профиль түзуі (2.1сурет а, б, в).
Горизонталь эпюрінің позициялық қасиеті: оның фронталь проекциясы ОХ өсіне параллель орналасуы.
Фронталь эпюрінің позициялық қасиеті: оның горизонталь проекциясы абсциссалар өсіне параллель орналасуы.
Проекция жазықтықтарына перпендикуляр түзулерді проекциялаушы түзулер деп атайды: горизонталь-проекциялаушы, фронталь-проекциялаушы және профиль-проекциялаушы, өздері перпендикуляр келген жазықтығына тәуелді.
Шындығында, егер де түзу қандайда бір жазықтыққа параллель болса, онда бұл жазықтыққа ол нақты өлшемімен проекцияланады. Сондықтан h1, f2, p3 – бұлар сәйкес h, f, p түзулерінің нақты өлшемі; α – π1 жазықтығына деңгей түзуінің көлбеу бұрышы; β – π2 жазықтығына деңгей түзуінің көлбеу бұрышы; γ – π1 жазықтығына деңгей түзуінің көлбеу бұрышы. Екі нүкте арқылы бір ғана түзу өтеді, сондықтан түзуді екі нүкте арқылы беруге болады. Мұндай түзу тапсырмасынан түзу кесінді тапсырмасына өту оңай. Шынында, сызғыш арқылы нүктелердің горизонталь проекциясын қосып, кесіндінің горизонталь проекциясын аламыз, нүктелердің фронталь проекцияларын қосып, кесіндінің фронталь проекциясын аламыз. Егер түзудің горизонталь және фронталь проекциялары берілсе, онда түзудің профиль проекциясын тұрғызу үшін осы түзудің кез келген екі нүктесінің профиль проекцияларын салу қажет және олар арқылы түзудің профиль проекциясын жүргізу керек. Деңгей сызығы қасиетінің біріне көңіл аудару керек. Деңгей сызығында орналасқан кесінді өзіне тең кесіндінің деңгей сызығына параллель келетін проекциялар жазықтықтарына проекцияланады.
Проекция жазықтықтарына перпендикуляр келген және қалған екі проекция жазықтығына перпендикуляр түзуді проекциялаушы түзу деп атайды.
Горизонталь проекция жазықтығына перпендикуляр түзу горизонталь проекциялаушы деп аталады. Фронталь проекция жазықтығына перпендикуляр түзу фронталь проекциялаушы деп аталады. Профиль проекция жазықтығына перпендикуляр түзу профиль проекциялаушы деп аталады.
Мысал. Горизонталь проекциялаушы түзудің сипаты, оның горизонталь проекциясы нүкте болып саналады, ал фронталь проекциясы ОХ өсіне перпендикуляр. Фронталь проекциялаушы түзудің сипаты, оның фронталь проекциясы нүкте болып саналады, горизонталь проекциясы ОХ өсіне перпендикуляр, ал профиль – нүкте. Проекцияланатын түзуде екі проекциясы проекция жазықтықтарына параллель. Сондықтан А2В2, А1В1, А1В1 және А2В2 – АВ түзуінің нақты өлшемі (2.2сурет).
а) б) в)
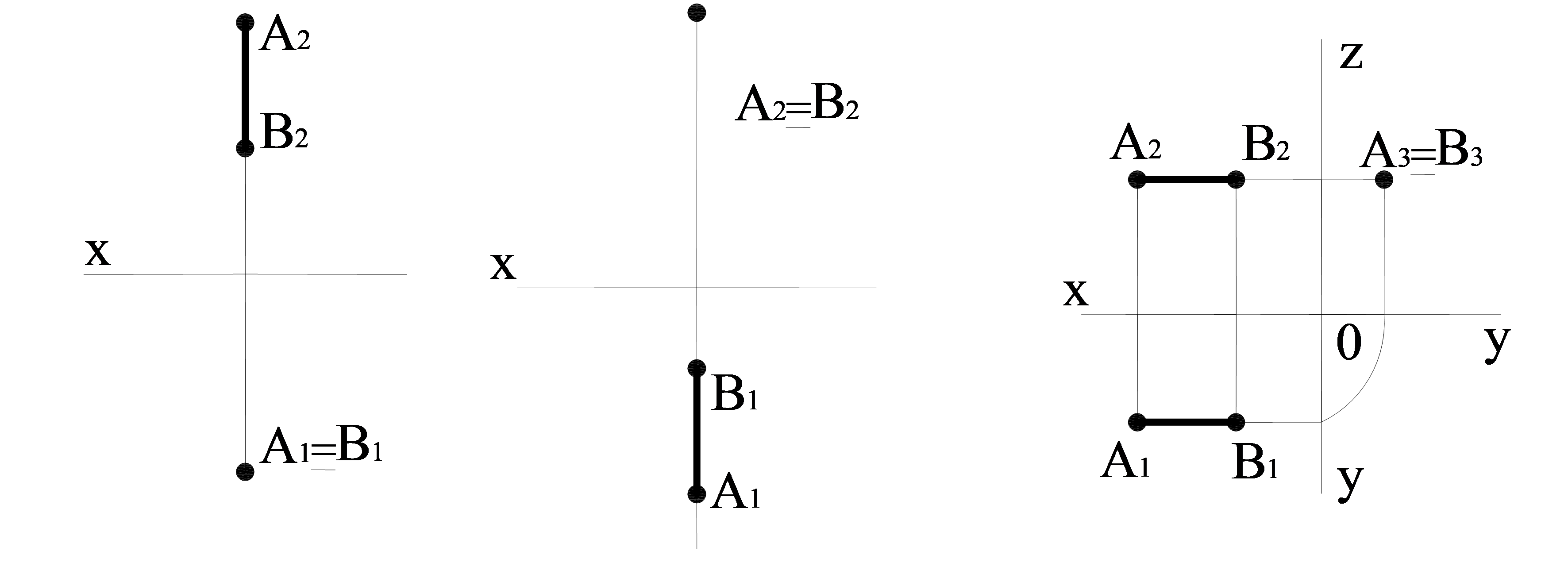
2.2 сурет – Проекция жазықтықтарына перпендикуляр түзулер
а) горизонталь проекциялаушы түзу: АВπ1; А2В2 –π1 жазықтығындағы АВ түзуінің нақты шамасы, АВ кесіндісі А1В1 нүктесінде проекцияланады; б) фронталь проекциялаушы түзу: АВ π2; А1В1 – π2 жазықтығындағы АВ түзуінің нақты шамасы, АВ кесіндісі А2В2 нүктесінде проекцияланады; в)профиль проекциялаушы түзу: АВ π3; А1В1 және А2В2 – АВ түзуінің нақты шамасы, А3В3 кесіндісі π3 жазықтығында нүкте түрінде проекцияланады
2.2 Блок. Түзу кесіндісінің нақты өлшемін және проекция жазықтықтарына көлбеулік бұрыштарын анықтау
Жалпы жағдайдағы түзу сызық кесіндісінің нақты өлшемін проекциялары арқылы анықтау үшін тікбұрышты үшбұрыш әдісін қолданады, оны келесідей қалыптастыруға болады: кесіндінің нақты өлшемі тікбұрышты үшбұрыш гипотенузасы болады, ал оның бір катеті кесіндінің горизонталь (фронталь) проекциясы болады, басқа катеті – кесіндінің фронталь проекциясының шет нүктесінен ОХ өсіне дейінгі қашықтық айырмасы болып табылады. Тікбұрышты үшбұрыштың гипотенузасы мен горизонталь (фронталь) проекция нүктесінің арасындағы бұрышы кесіндінің горизонталь жазықтық проекциясына көлбеу бұрышы болып табылады.
Мысал. π 1 және π 2 жазықтығына қатысты жалпы жағдайдағы АВ кесіндісі берілген. АВ1В – тікбұрышты үшбұрышы, онда катеттері АВ1=А1В1, ал ВВ1 катеті z-ке тең, ол А және В нүктелерінің π1 жазықтығына дейінгі қашықтық айырмасы (2.3сурет).
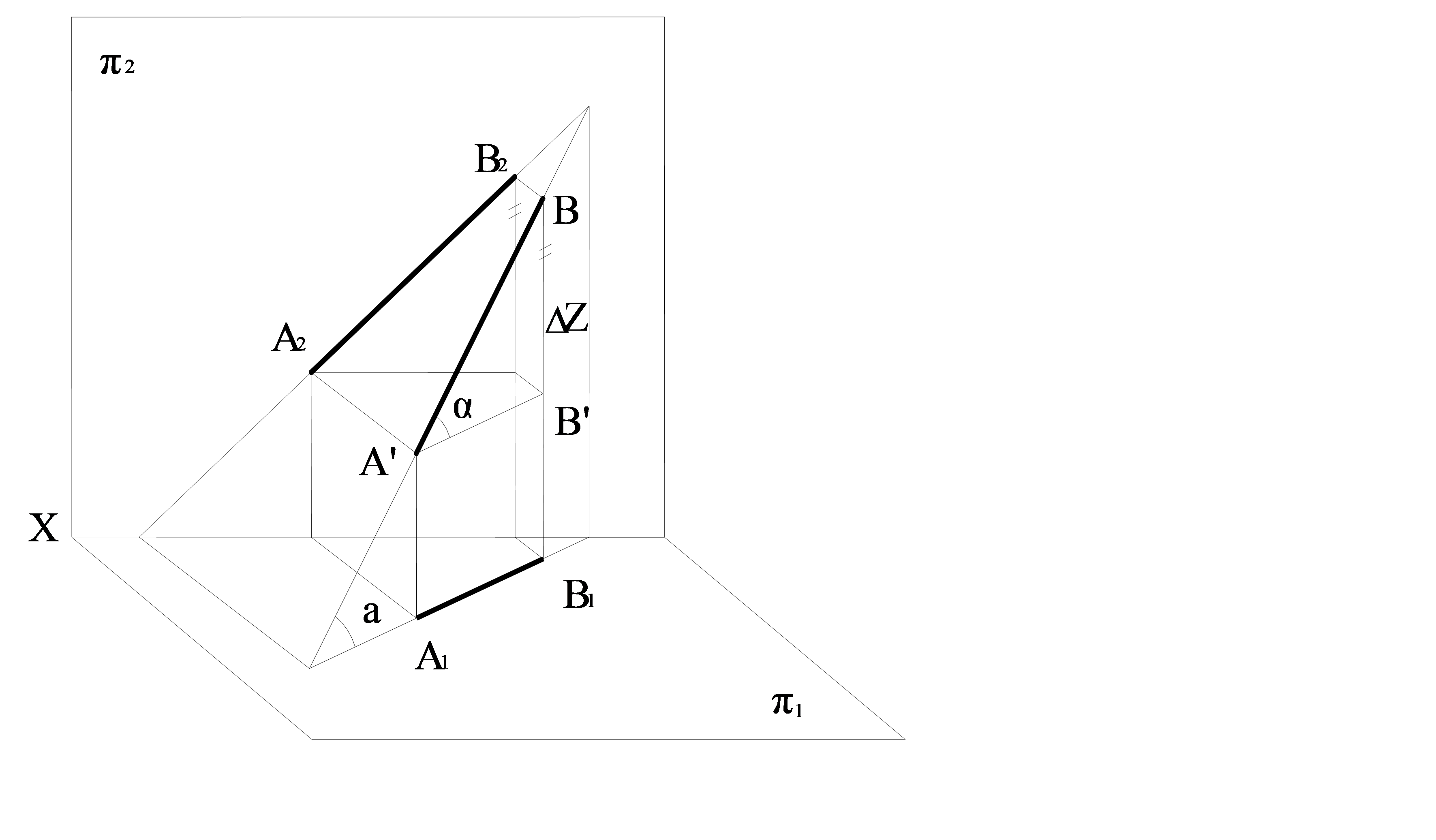
2.3 сурет – АВ кесіндінің нақты өлшемін және π1 проекция жазықтықтығына көлбеулік бұрышын анықтау
α – π1 проекция жазықтығына қатысты АВ түзуінің көлбеулік бұрышы; АВ түзуі – жалпы жағдайдағы түзуі; π1 және π2 – горизонталь және фронталь проекциялар жазықтығы
АВ1В тікбұрышты үшбұрышында α бұрышы π 1 жазықтығына АВ түзуінің көлбеулік бұрышын анықтайды. Осылай жалпы жағдайдағы түзу кесіндісінің нақты өлшемі тік бұрышты үшбұрыштың гипотенузасымен анықталады. Оның бір катеті кесіндінің проекциясына тең, ал екінші катеті кесінді соңынан проекция жазықтығының біріне дейінгі қашықтығының алгебралық айырмасына тең.
2.3 Блок. Түзудің кесіндісін тең бөліктерге бөлу>
Кесіндіні берілген қатынаста бөлуде Фалестің теоремасы қолданылады: егер бұрыштың бір жағынан кесіндіге тең немесе пропорционал және белгіленген белгісі арқылы кез келген параллель түзулер жүргізсе, онда басқа жағы да тең және пропорционал кесінділерге бөлінеді. Нүктелердің проекциялары кесінділердің аттас проекцияларын қандай қатынаста бөлсе, сондай қатынаста нүкте түзу сызықтың кесіндісін кеңістікте бөледі.
Мысал. 2:3 қатынасында АЕ кесіндісін тең бөлікке бөлу керек, бөлетін нүкте кесіндіде жатыр (2.4сурет). Алдымен сызбада 2:3 қатынаста берілген АЕ кесіндінің А1Е1 горизонталь проекциясын бөлетін D1 нүктенің горизонталь проекциясын табамыз. Ол үшін А1 нүктесі арқылы бір түзу жүргіземіз, осы түзу үстінен А1 нүктесінен бастап бес өзара тең кесінділер өлшеп саламыз (2+3=5). Содан соң K* және Е1 нүктелерін түзу сызық арқылы қосамыз және K*Е1 түзуіне параллель болатын 2D түзу жүргіземіз. D1 нүктесі А1Е1 кесіндісін 2:3 қатынасымен бөледі. Байланыс сызығын жүргізіп, D нүктенің D2 фронталь проекциясын табамыз. D2 нүктесі А2Е2 кесіндісін D2А2/ D2Е2 = 2/3 қатынысымен бөледі.
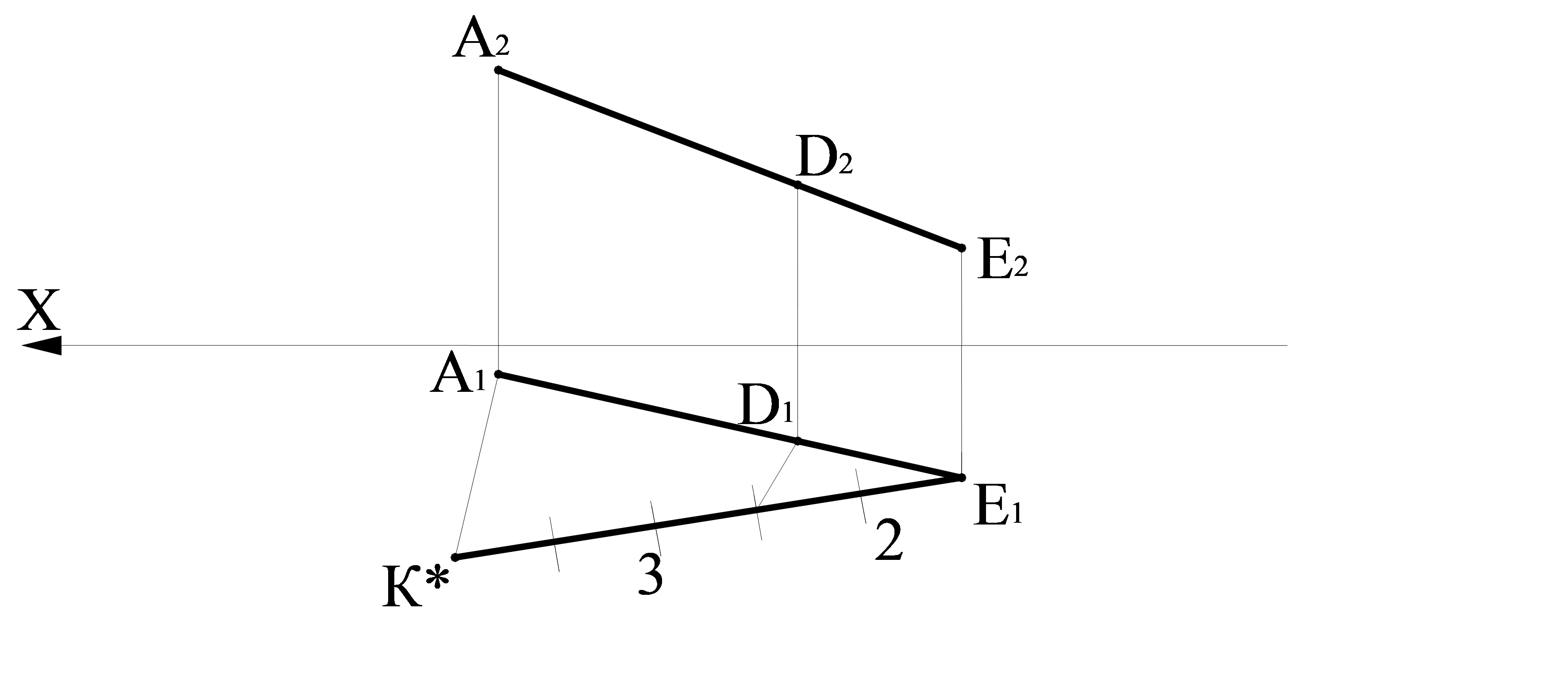
2.4 сурет – АЕ кесіндіні 2:3 қатынасында бөлу
2.4 Блок. Түзудің ізі
Жалпы жағдайдағы түзу барлық негізгі проекциялар жазықтықтарын қиып өтеді. Түзудің проекция жазықтығымен қиылысу нүктелерін түзудің іздері деп атайды. Түзудің қандай проекциялар жазықтықтарымен қиылысатынына байланысты іздерді горизонталь, фронталь және профиль деп атайды. Түзу іздерінің проекцияларына сәйкес М1 – горизонталь іздің горизонталь проекциясы, М2 – фронталь іздің фронталь проекциясы деп белгіленеді. М1 проекциясы М горизонталь ізге сәйкес келетінін ескерсек, ал оның М2 фронталь проекциясы ОХ өсінде жатады. N фронталь ізі N2 фронталь іздің фронталь проекциясымен сәйкес келеді, ал оның N1 горизонталь проекциясы ОХ өсінде жатады.
Мысал. Жалпы жағдайдағы СD түзуі берілген, түзудің ізін салу керек (2.5сурет). Түзудің горизонталь ізін табу үшін С2D2 фронталь проекциясын ОХ өсінің қиысуына дейін жалғастыру керек. Алынған М2 нүктесі горизонталь іздің фронталь проекциясы болады.
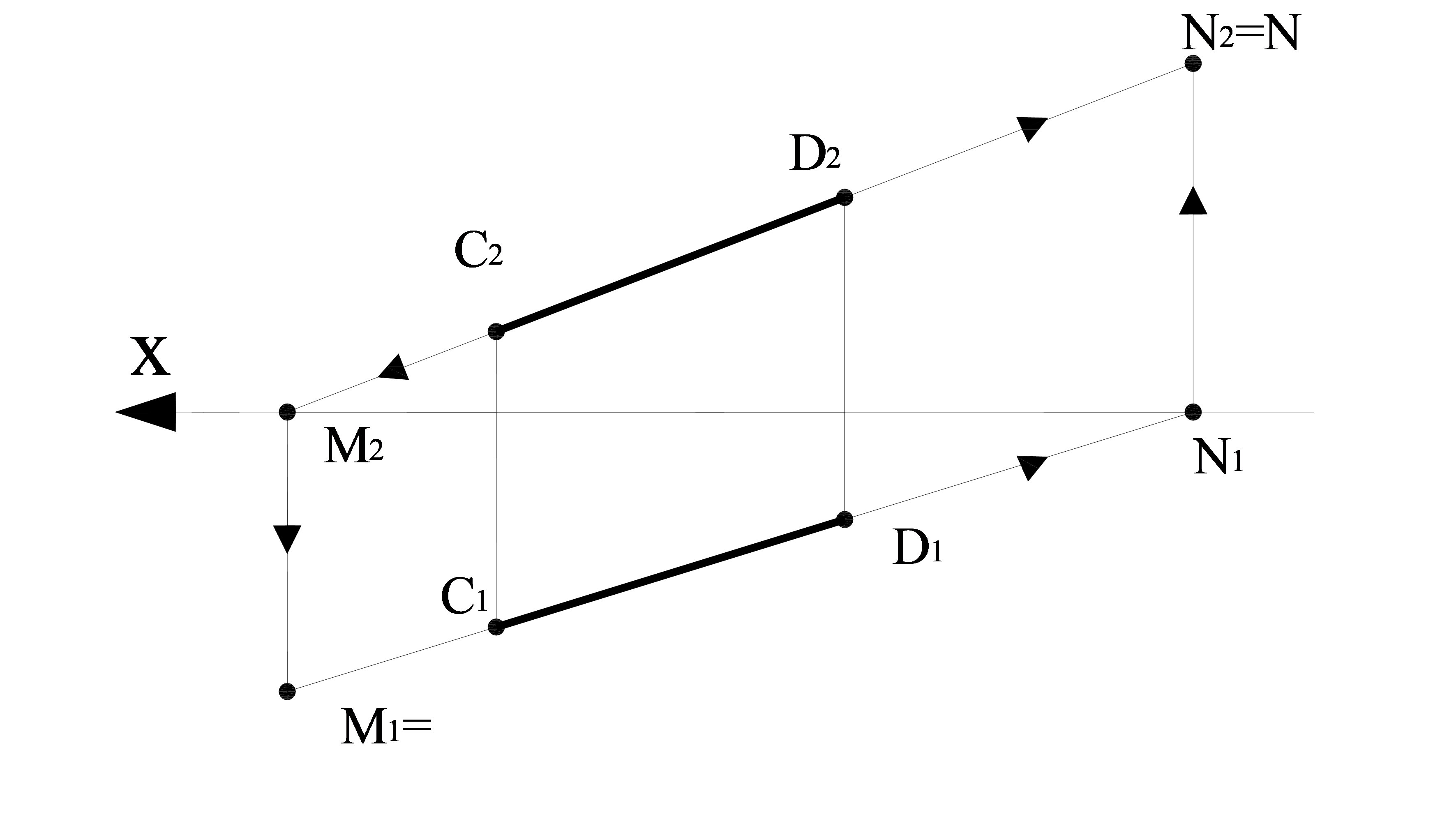
2.5 сурет – СD түзудің іздерің тұрғызу
N – фронталь із; N1 – фронталь іздің горизонталь проекциясы;
N2 – фронталь іздің фронталь проекциясы; М – горизонталь ізі; М1 – горизонталь іздің горизонталь проекциясы; М2 – горизонталь іздің фронталь проекциясы.
Табылған нүктеден ОХ өсіне С1D1 кесіндінің горизонталь проекциясымен қиылысуына дейін перпендикуляр жүргіземіз. М1 нүктесі –горизонталь іздің горизонталь проекциясы, ол горизонталь іздің өзіне сәйкес келеді. Фронталь ізін табу үшін С1D1 түзудің горизонталь проекциясын ОХ өсімен қиылысқа дейін жалғастырамыз, С2D2 түзудің фронталь проекциясымен қиылысқанға дейін N1 (фронталь іздің горизонталь проекциясы) арқылы перпендикуляр жүргіземіз. N2 нүктесі – фронталь іздің фронталь проекциясы, ол N фронталь ізбен сәйкес келеді.
Егер түзу проекция жазықтығына параллель келсе, мұндай жағдайда түзудің осы проекция жазықтығында ізі болмайды.
2.5 Блок. Түзулердің кеңістіктегі өзара орналасуы. Бәсекелес нүктелер
Түзулер кеністікте өзара параллель, қиылысқан, айқас орналасуы мүмкін. Түзудің профиль проекциясын екі түзуімен құрастыруға мүмкін болғандықтан, екі көріністі жазықтық сызбамен шектелеміз.
Ортогональ проекциялау қасиетінің біріне сәйкес, егер де түзулер параллель болса, онда олардың аттас проекциялары да параллель болады.
Мысал. Берілген АВ және DЕ параллель түзулер арқылы горизонталь жазықтық проекциясына перпендикуляр жазықтық өткізсек, онда бұл екі жазықтық параллель болады, және олардың π 1 жазықтығымен қиылысуында А1 В1мен D1E1 өзара екі параллель түзуі алынады. Ол түзулер АВ және DE түзуінің горизонталь жазықтық проекциясына ортогональ проекциясы болады (2.6 сурет).
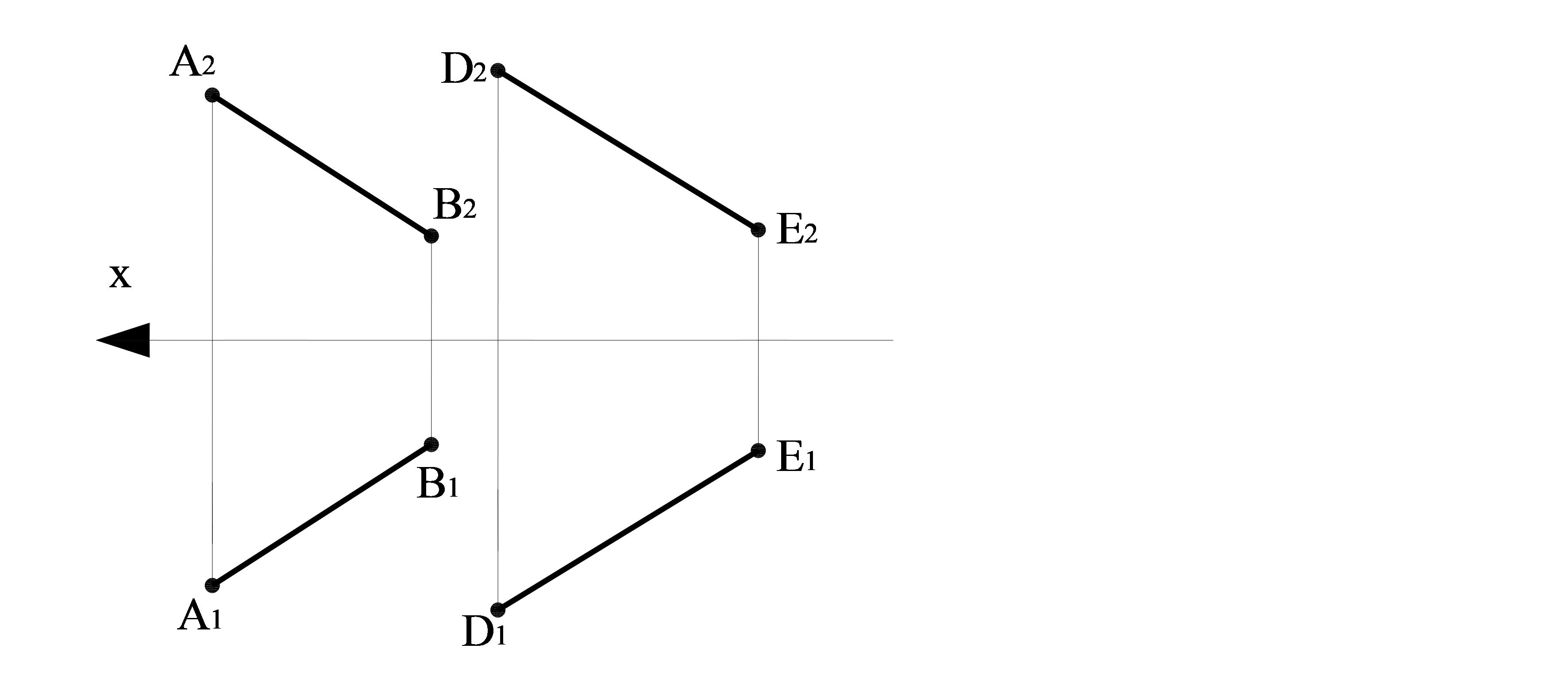
2.6 сурет – АВ және DЕ өзара параллель түзулерінің проекцияларын салу
А1В1 – АВ түзудің горизонталь проекциясы; А2В2 – АВ түзудің фронталь проекциясы; D1E1 – DE түзудің горизонталь проекциясы; D2E2 – DE түзудің фронталь проекциясы
Қиылысатын түзулер деп ортақ нүктесі – қиылысу ортақ нүктесі бар түзулерді айтады (2.7 сурет). Қиылысу нүктесінің проекциясы бір байланыс сызығында жатады, бұл – эпюрада қиылысатын түзулердің белгісі болып табылады.

2.7 сурет –АВ және CD қиылысқан түзулерінің проекциясы
Перпендикуляр түзулер қиылысатын түзулердің дербес жағдайы болып табылады (2.8 сурет). Түзу бұрышты проекциялау теориясына сәйкес түзу нақты шамаға жазықтық проекциясында келесі жағдайда проекцияланады: егер жазықтық проекциясының бір жағы осы жазықтық проекциясына параллель болса.

2.8 сурет – СD және DE перпендикуляр түзулерінің проекциялары
С1D1 – СD түзудің горизонталь проекциясы; D2Е2 – СD түзудің фронталь проекциясы; С2D2 – СD түзудің фронталь проекциясы; D1Е1 – СD түзуінің горизонталь проекциясы.
Өзара параллель емес және қиылыспайтың түзулерді айқас түзулер деп атайды. Айқас түзулер кеңістікте қиылыспайды, бірақ эпюрде олардың біраттас проекциялары бір-біріне айқасады, осыдан қиылысу пікірі туады (2.9 сурет).
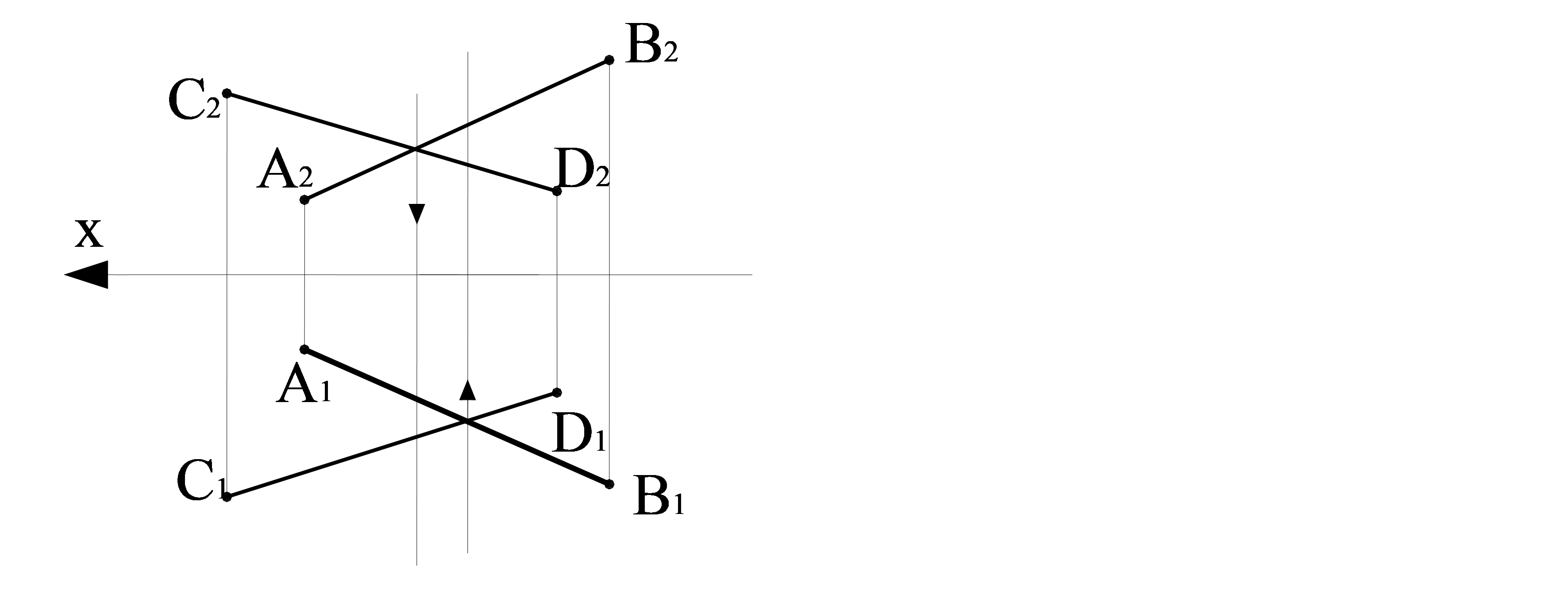
2.9 сурет – СD және АВ айқас түзулер
С1D1 – СD түзуінің горизонталь проекциясы; А2В2 – АВ түзуінің фронталь проекциясы; С2D2 – СD түзуінің фронталь проекциясы; А1В1 – АВ түзуінің горизонталь проекциясы
Проекциялардағы айқастың түзулердің белгісі: олардың жорамал қиылысу нүктелерінің проекциялары бір байланыс сызығында жатпайды.
Жорамал қиылысу нүктелерде екі нүкте бәсекелес болады. Жорамал нүктелерде екі түзу бәсекелес болады. Бұл шетті бәсекелес орны деп атаймыз. Тоғысатын түзулерді қарастырғанда бәсекелестік орындарда түзудің проекцияларының көзге көрінетіні жайлы сұрақ туындайды. Бұл сұрақты бәсекелестік нүктелер әдісі арқылы шешуге болады. Әдістің қорытындысы:
- қарастырылып отырған проекцияларда бәсекелестік орнын белгілеу;
- бәсекелестік нүктесін белгілеу немесе қандай түзулер бәсекелесетінін жазу;
- байланыс сызығының бойында бәсекелестік нүктелердің немесе түзулердің жетпейтін координаттарын салыстыру;
- қарастырып отырған проекцияда жетпей тұрған координаты бар нүкте немесе түзу көрінеді.
Горизонталь проекциялары сәйкес келетін нүктелер горизонталь бәсекелес нүктелер, ал егер фронталь проекциялары сәйкес келсе, онда фронталь бәсекелес нүктелер деп аталады.
Мысал. А және b айқас түзулер берілген (2.10 сурет). Қандай түзу көрінетінін табу керек.
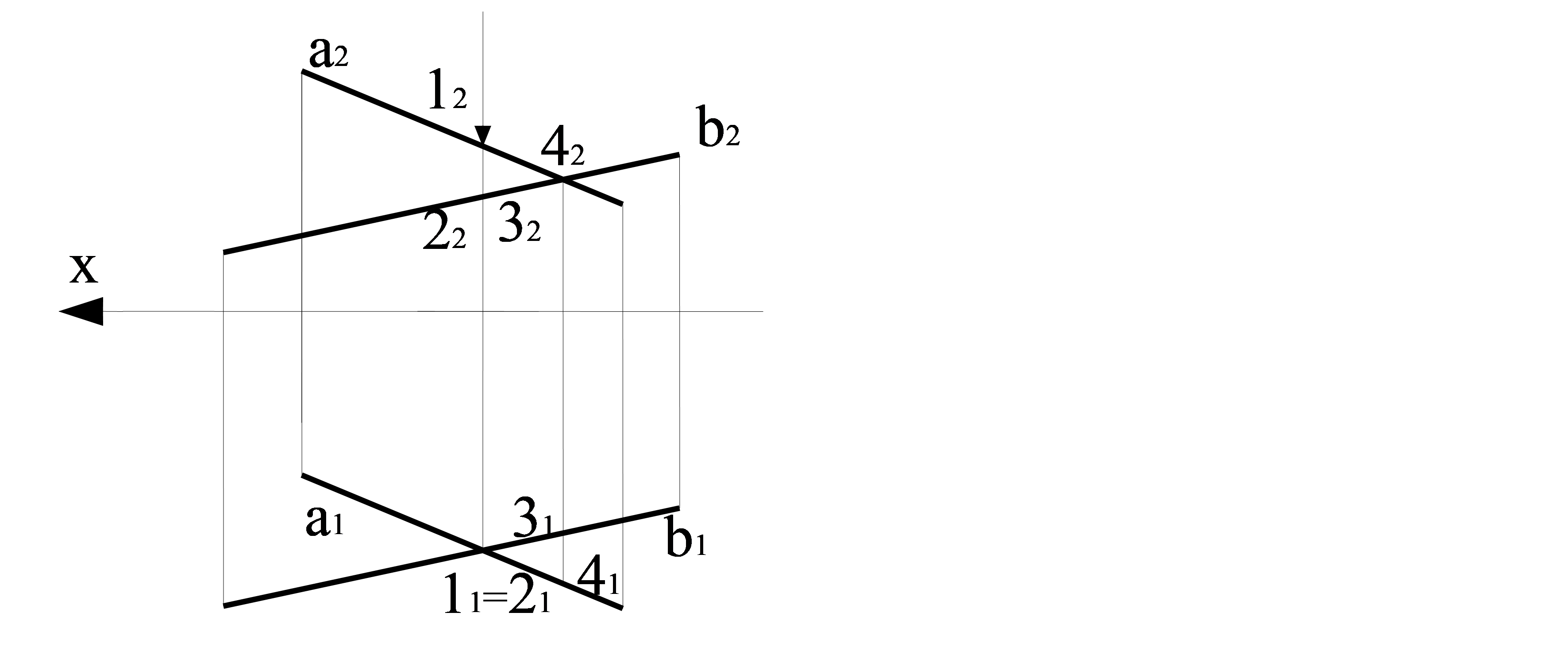
2.10 сурет – Бәсекелес нүктелер әдісі бойынша түзулердің көрінісін анықтау
а1 және b1 – а және b түзулерінің горизонталь проекциясы; а2 және b2 – а және b түзулерінің фронталь проекциясы; 1 және 2 – бәсекелес нүктелер
2.10 суретте горизонталь проекцияда а түзуінде жататын 1 нүктесі көрініп тұрады. Фронталь проекцияда а түзуі де көрініп тұрады, сондай-ақ олардың бәсекелес орнында көп координаттар бар.
Ұсынылған теориялар төмендегі жағдайларға негізделеді:
1) Монж теориясының негізінде тек қана нүктенің ғана емес, сонымен қатар күрделі обьектілердің, соның ішінде түзу сызығының және оның кесіндісінің кеңістікті бейнесін түрлендіруге болады;
2) СD кесіндісінің проекциясын алу үшін оның С және D нүктелерінің соңының проекцияларын салады – С1D1; С2D2; С3D3. Нүктелердің аттас проекцияларын қосу арқылы π1 жазықтығынан С1D1 кесіндісінің проекциясын; π2 жазықтығынан – С2D2; π3 жазықтығынан – С3D3 кесіндісінің проекциясын алады. Кесінділер соңының проекциялары проекциялық байланыс сызықтарымен байланысты;
3) нүкте кесіндіде жатады, егер де оның проекциялары сол түзудің аттас проекцияларында орналасса;
4) түзудің кесіндісі проекция жазықтықтарына қатысты келесідей бөлінеді:
- жалпы жағдайдағы түзулер;
- деңгей тузулері (қандай да бір проекция жазықтығына параллель);
- проекциялаушы тузулер (қандай да бір проекция жазықтығына перпендикуляр).
5) кесінді π1, π2 және π1, π2, π3 жүйелерінде берілуі мүмкін;
6) берілген екі проекциясы арқылы әрқашанда үшіншісін салуға болады;
7) кеңістіктегі кесінді проекция жазықтығындағы ұзындығымен және көлбеу бұрышымен сипатталады;
8) деңгей кесіндісі үшін және проекциялайтын кесінділер үшін бұл өлшемдер кешенді сызбаларда анықталады, себебі дербес жағдайдағы кесіндінің бір проекциясы осы кесіндінің нақты өлшемі;
9) жалпы жағдайдағы кесіндінің нақты өлшемін және проекция жазықтығына көлбеу бұрышын табу үшін тікбұрышты үшбұрыш әдісі қолданылады.
Тапсырмалар:
1 есеп. Берілген координаттары бойынша СD кесіндісінің проекцияларын тұрғызыңыз: С (15; 25; 10), D (24;60;25);
2 есеп. А (15;25;45), В(60;25;5) түзудің эпюрасын тұрғызыңыз.
Өзіндік талдау үшін сұрақтар
1) Егерде түзу қандайда бір проекция жазықтығына параллель келсе қасиеті неде?
2) Түзудің қандай проекциясы ОХ өсіне параллель келеді, егер де осы түзу π 1 жазықтығына параллель келсе?
3) Егерде түзудің бір проекциясы нүкте болса, онда бұл қандай түзу болғаны?
4) Қашан түзу жазықтыққа нақты өлшеммен проекцияланады?
5) Жалпы жағдайдағы кесіндінің нақты өлшемі қалай анықталады?
6) z∆ және y∆ нені анықтайды?
7) Бір проекция жазықтығына тиісті түзудің проекциясы қалай орналасады?
8) Кешенді сызбада жалпы жағдайдағы түзуді деңгей түзуіне және проекциялайтын түзуге қалай түрлендіруге болады?
9) Кеңістікте тоғыспалы және қиылысатын түзулер қалай орналасады?
10) Тоғыспалы және қиылысатын түзулердің проекциясының кешенді сызбадағы орнының ұқсастығы мен айырмашылығы неде?
11) Бәсекелес нүктелер дегеніміз не?
12) Егер кеңістікте екі түзудің екі ортақ нүктесі болса, онда олар қиылысады. Бұл тұжырым дұрыс па?
13) Екі тоғыспалы және параллель түзулердің бәсекелес нүктелерінің орналасуына мысал келтіріңіз.
14) Кеңістіктегі түзулердің параллельдігін анықтау үшін неше проекциясын берілуі керек?
Бақылау жұмысы
1есеп. Координата бойынша С (5, 25, 43) және D (25, 60, 15) түзудің координаттары берілген. Түзудің проекциясын салу және проекция жазықтығына қатысты түзудің қалай орналасқанын анықтау қажет.
2есеп. АВ түзуінің ізің тұрғызу қажет ( 2.11сурет).
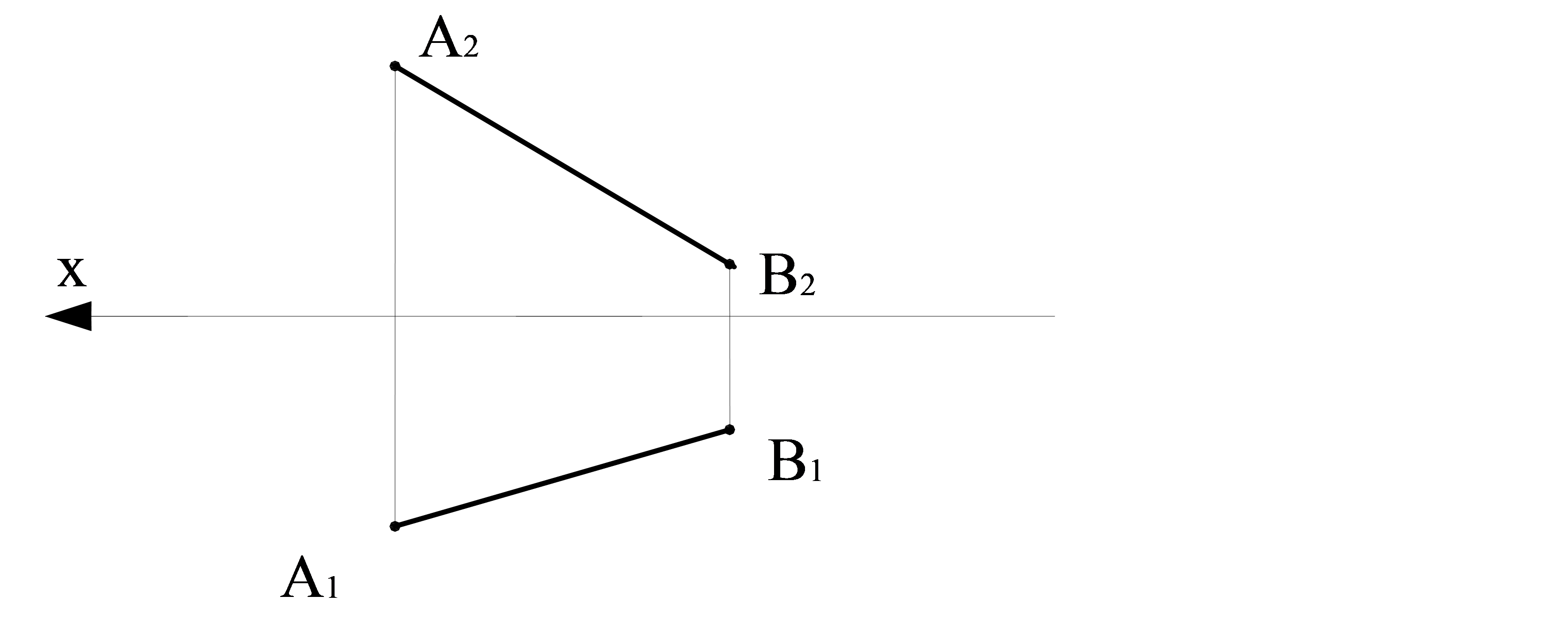
2.11сурет – СD түзуінің ізі
Әдебиеттер
Негізгі:
1 Есмуханов Ж. М. Сызба геометриясы есептері. – Алматы: Білім,1995. – 272 б.
2 Ақпанбек Ғ. Сызба геометрия. – Алматы,1998. – 208б.
3 Ақпанбеков Ғ. Сызба геометрия. – Алматы: «Қазақ универсиверситеті», 1992. – 120 б.
4 Миронова Р.С., Миронов Б.Г. Сборник заданий по черчению. – М.: Высшая школа, 2004. – 355 с.
Қосымша
5 Чекмарев А.А. Инженерная графика. – М.: Высшая школа, 1988. – 365с.
6 Короев Ю.И.Черчение для строителей. – М.: Стройиздат, 2001. – 256 с.
7 Крылов Н.Н. Начертательная геометрия. – М.: Высшая школа, 2005. – 224 с.