Модуль. Жазықтықтар
3.1 Блок. Сызбада жазықтықтың орналасуы
Жазықтық кешенді сызбада геометриялық элементтермен берілуі мүмкін, олар жазықтықтардың кеңістіктегі орнын анықтайды:
- бір түзудің бойында жатпайтын үш нүкте (3.1 а сурет); түзу және одан тысқары нүкте (3.1 б сурет); екі параллель түзу (3.1в сурет); жазық фигура (3.1г сурет); екі қиылысушы түзулер (3.1е сурет).
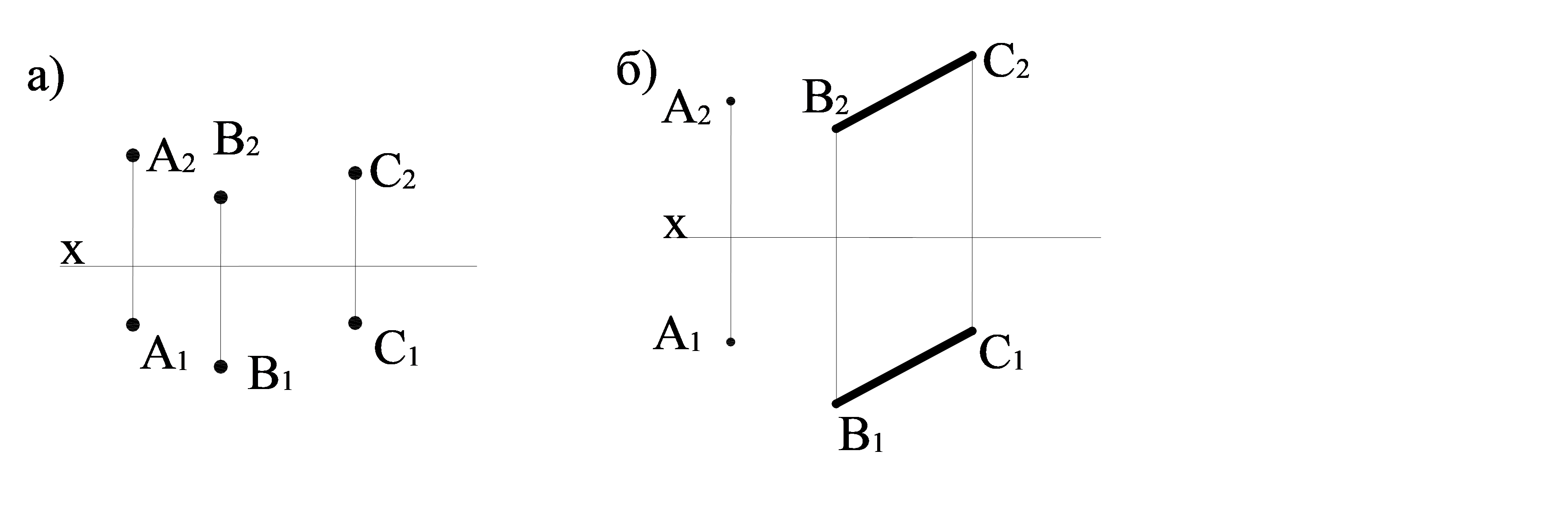
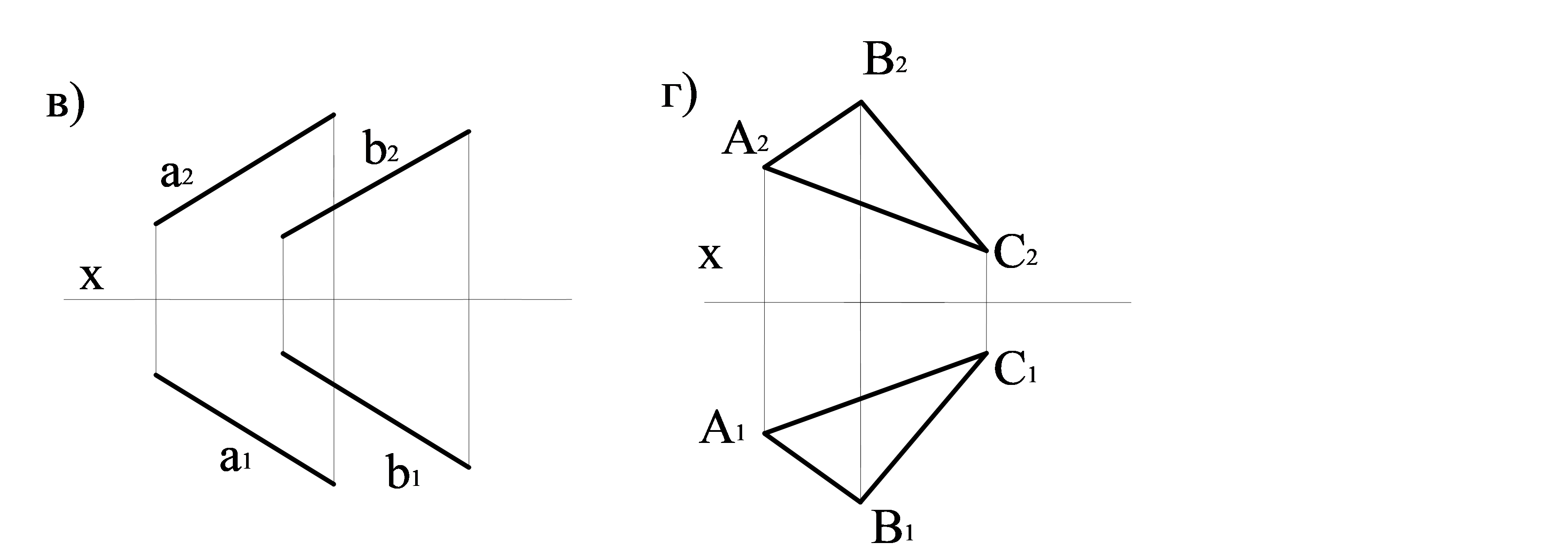

3.1сурет – Кешенді сызбада жазықтықтың проекциялары
3.2 Блок. Жазықтықтың проекция жазықтықтарына қатысты орналасуы
Кеңістікте орналасуына қарай жазықтық жалпы және дербес жағдайда болады. Жазықтық ешқандай проекция жазықтығына перпендикуляр немесе параллель болмаса, онда жалпы жағдайдағы жазықтық деп аталады.
Мысал. АВС үшбұрышымен берілген жазықтық проекция жазықтығына не перпендикуляр емес, не параллель емес.
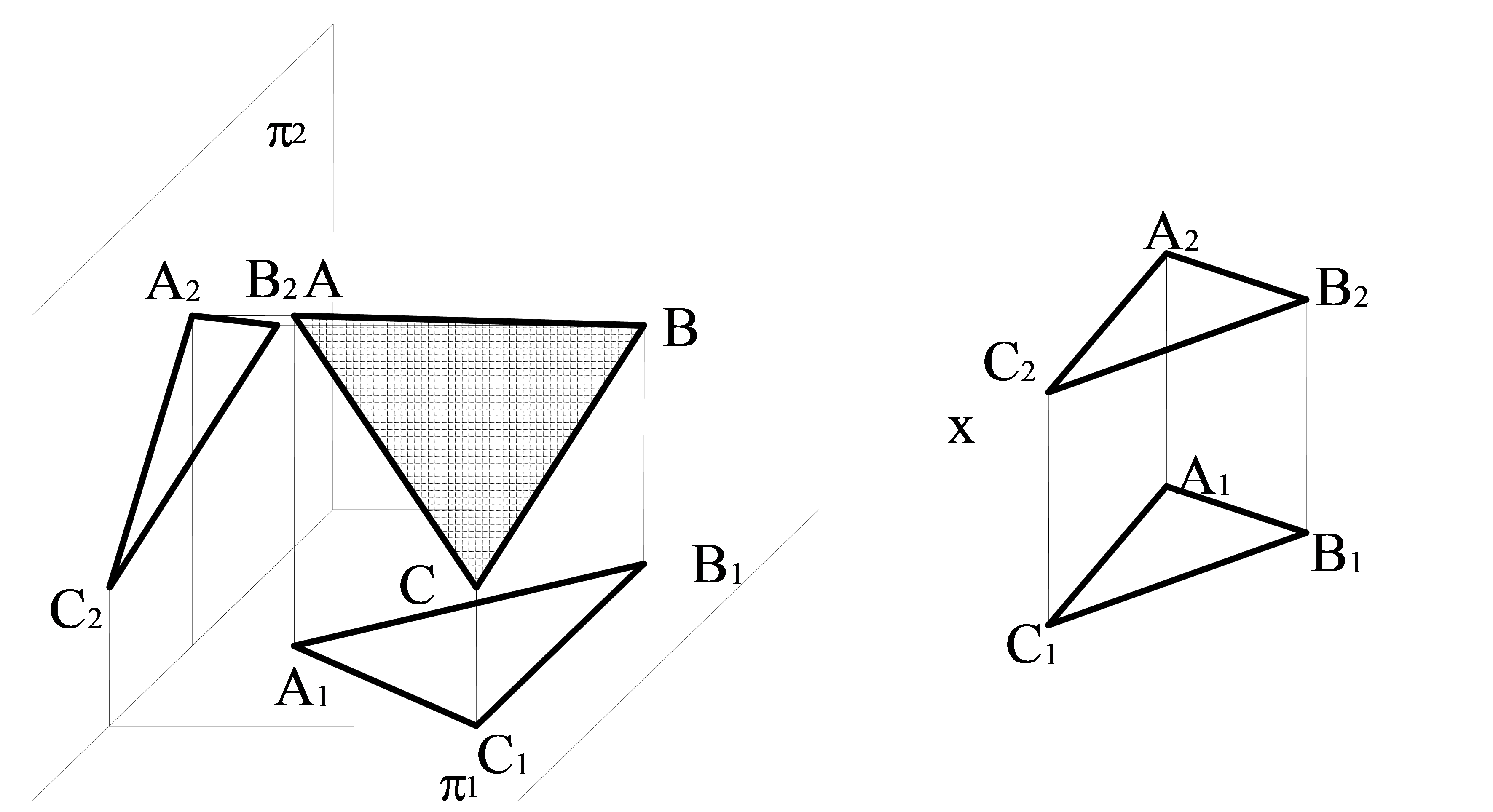
3.2 сурет – Жалпы жағдайдағы АВС үшбұрышмен берілген жазықтықтың проекциясы
А1В1С1 – АВС жазықтығының горизонталь проекциясы; А2В2С2 – АВС жазықтығының фронталь проекциясы; π1 – горизонталь проекция жазықтығы; π2 – фронталь проекция жазықтығы
Егер жазықтық проекция жазықтығының біріне перпендикуляр немесе параллель болса, онда дербес жағдайдағы жазықтық деп аталады. Дербес жағдайдағы жазықтықтар проекциялаушы және деңгейлік жазықтықтары деп екіге бөлінеді (3.3сурет).
Проекциялаушы жазықтықтар проекция жазықтықтарына беруіне перпендикуляр орналасады.
Горизонталь проекциялаушы жазықтық деп – горизонталь проекция жазықтығына перпендикуляр жазықтықты атайды.
Мысал. АВС үшбұрышымен берілген жазықтық горизонталь жазықтығына перпендикуляр. Бұл жазықтықта жатқан кез келген элемент горизонталь жазықтығына түзу сызықпен проекцияланады; A1B1C1 үшбұрышының горизонталь проекциясы горизонталь жазықтығындағы түзу сызық болады (3.3 а сурет).
Фронталь проекциялаушы жазықтық деп – фронталь проекция жазықтығына перпендикуляр жазықтық аталады.
Мысал. АВС үшбұрышымен берілген жазықтық фронталь проекция жазықтығына перпендикуляр. Бұл жазықтықта жатқан кез келген элемент фронталь жазықтығына түзу сызықпен проекцияланады; A2B2C2 үшбұрышының фронталь проекциясы фронталь проекция жазықтығындағы түзу сызық болады (3.3 б сурет).
Профиль проекциялаушы жазықтық деп– профиль проекция жазықтығына перпендикуляр жазықтық аталады.
Мысал. АВС үшбұрышымен берілген жазықтық профиль проекция жазықтығына перпендикуляр(3.3 в сурет).
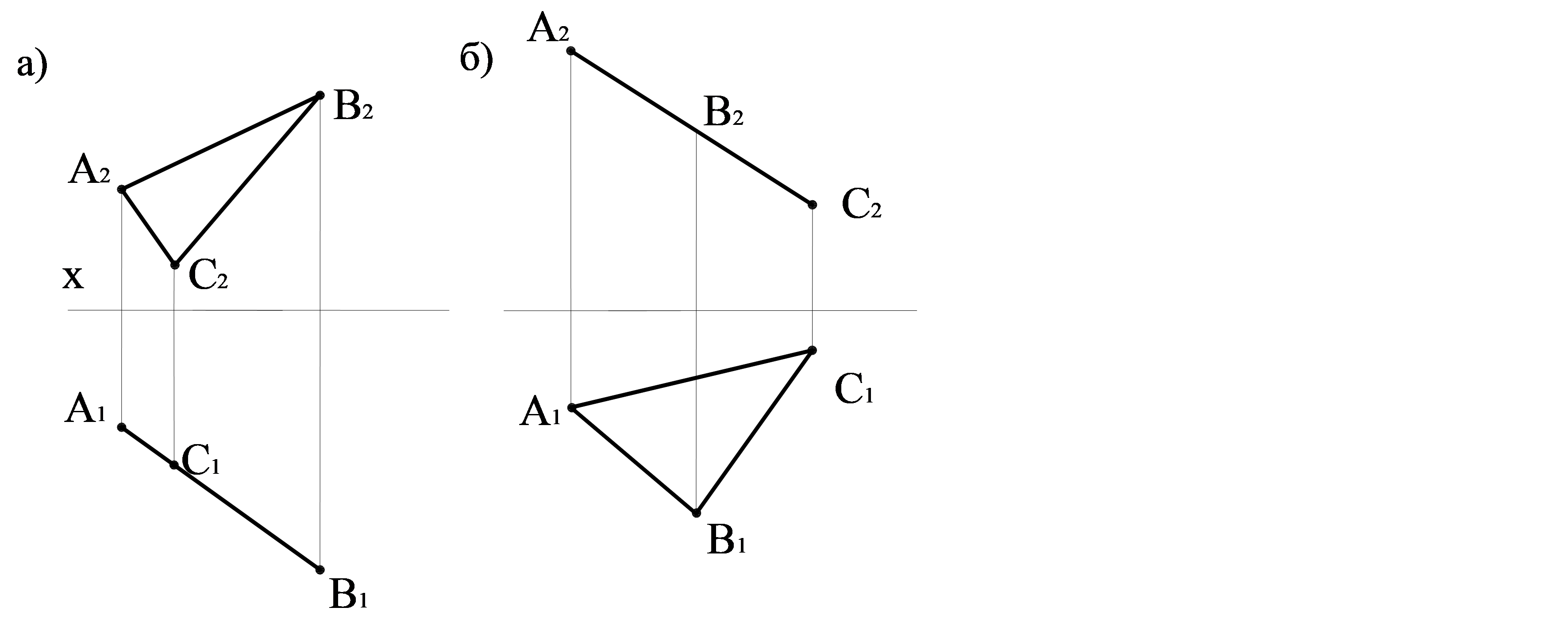

3.3 сурет – Дербес жағдайдағы жазықтық проекциялары
а) АВСD горизонталь проекциялаушы жазықтық: АВС ^ π 1; б) АВСD фронталь проекциялаушы жазықтық: АВС ^ π 2; в) АВСD профиль проекциялаушы жазықтық: АВС ^ π 3.
Бұл жазықтықта жатқан кез келген элемент профиль проекция жазықтығына түзу сызықпен проекцияланады; A3B3C3 үшбұрышының фронталь проекциясы профиль проекция жазықтығындағы түзу сызық болады.
Сонымен, егер жазықтық проекция жазықтарының біріне перпендикуляр болса, онда ол осы жазықтыққа түзу сызық түрінде проекцияланады.
Проекция өсі бойынша өтетің жазықтықтарды өстік проекциялаушы жазықтықтар деп аталады. Егер өстік проекциялаушы жазықтықтардың проекция жазықтықтарына көлбеу бұрыштары өзара тең болса, онда биссектор жазықтығы деп атайды.
Проекция жазықтықтарына біреуіне параллель орналасқан жазықтықтар деңгейлік жазықтықтар деп аталады және қалған екі проекция жазықтығына перпендикуляр орналасады. Бұл жазықтықтардың сипаттық ерекшеліктері: осы жазықтықта орналасқан элементтер сәйкес проекция жазықтығында нақты өлшеммен проекцияланады.
Горизонталь жазықтығы – горизонталь проекция жазықтығына параллель жазықтық аталады.
Мысал. АВС үшбұрышымен берілген жазықтық горизонталь проекция жазықтығына параллель, осы жазықтық ОХ өсіне параллель фронталь проекция жазықтығын қияды, ал профиль проекция жазықтығы – ОУ өсіне параллель (3.4а сурет).
Фронталь жазықтығы – фронталь проекция жазықтығына параллель жазықтық аталады.
Мысал. АВС үшбұрышымен берілген жазықтық фронталь проекция жазықтығына параллель, осы жазықтық ОХ өсіне параллель горизонталь проекция жазықтығын қияды, ал профиль проекция жазықтығы – OZ өсіне параллель сызық бойынша (3.4 б сурет).
Профиль жазықтығы – профиль проекция жазықтығына параллель жазықтық аталады.
Мысал. АВС үшбұрышымен берілген жазықтық профиль проекция жазықтығына параллель, осы жазықтық Z өсіне параллель сызық бойынша горизонталь проекция және фронталь проекция жазықтықтарын қияды (3.4в сурет). Сонымен, егер жазықтық кез келген прокция жазықтығына параллель болса, онда ол осы жазықтыққа нақты өлшеммен проекцияланады, ал оның басқа екі проекциясы проекция өсіне параллель түзу сызықтары болады.
(π 1 π 2) жүйесіндегі жазықтықтың кешенді сызбасынан (π 1π 2π 3) жүйесіндегі жазықтықтың кешенді сызбасына ауысу үшін, жазықтықта берілетін фигуралардың профиль проекциясын салу қажет.
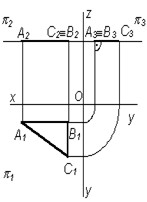
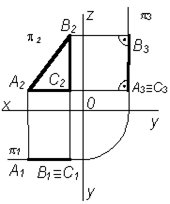
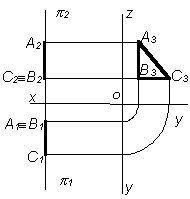
3.4 сурет – Деңгейлік жазықтықтарының проекциясы
а) АВС горизонталь деңгейлік жазықтығы; б) АВС фронталь деңгейлік жазықтығы; в) АВС профиль деңгейлік жазықтығы
Денгейлік жазықтықта жататын фигуралардың проекцияларының қасиеттері көптеген метрлік және позициялық есептерді шығарғанда қолданады. Денгейлік жазықтықтар екі проекция жазықтығына перпендикуляр болдғандықтан екі рет проекциялаушы болып саналады.
3.3 Блок. Жазықтықтағы нүктелердің, түзулердің көрінісі
Егер жазықтықтың кез келген екі нүктесі арқылы түзу тұрғызылғанға мүмкін болса, онда осы түзудің барлық нүктесі сол жазықтықта жатады.
Түзуідің жазықтықта жататындары екі белгінің біреуі бойынша анықталады:
- түзу осы жазықтықта жататын екі нүкте арқылы өтеді;
- түзу жазықтықта жатқан нүкте арқылы өтеді және де осы жазықтықта жатқан түзуге параллель.
Мысал. 3.5 суретте жалпы жағдайдағы жазықтық АВС үшбұрышымен берілген. А, В, С нүктелері осы жазықтыққа жатады, себебі осы жазықтықтағы үшбұрыштың төбелері болып табылады. (АВ), (ВС), (АС) түзулері жазықтыққа жатады, себебі олардың екі нүктесі жазықтықта жатыр. Ν нүктесі (АС)- ға, D нүктесі (АВ)- ға, Е нүктесі (СD)- ға жатады, демек Ν және Е нүктелері (∆АВС) жазықтығына жатады, онда (ΝЕ) түзуі (∆АВС) жазықтығына жатады.
Егер L нүктесінің бір проекциясы берілген болса, мысалы L2 нүктесі және (∆АВС) жазықтығына L нүктесінің жататыны белгілі болса, онда L1 нүктесінің екінші проекциясын табу үшін ретімен (А2L2), К2,(А1К1), L1 табамыз.
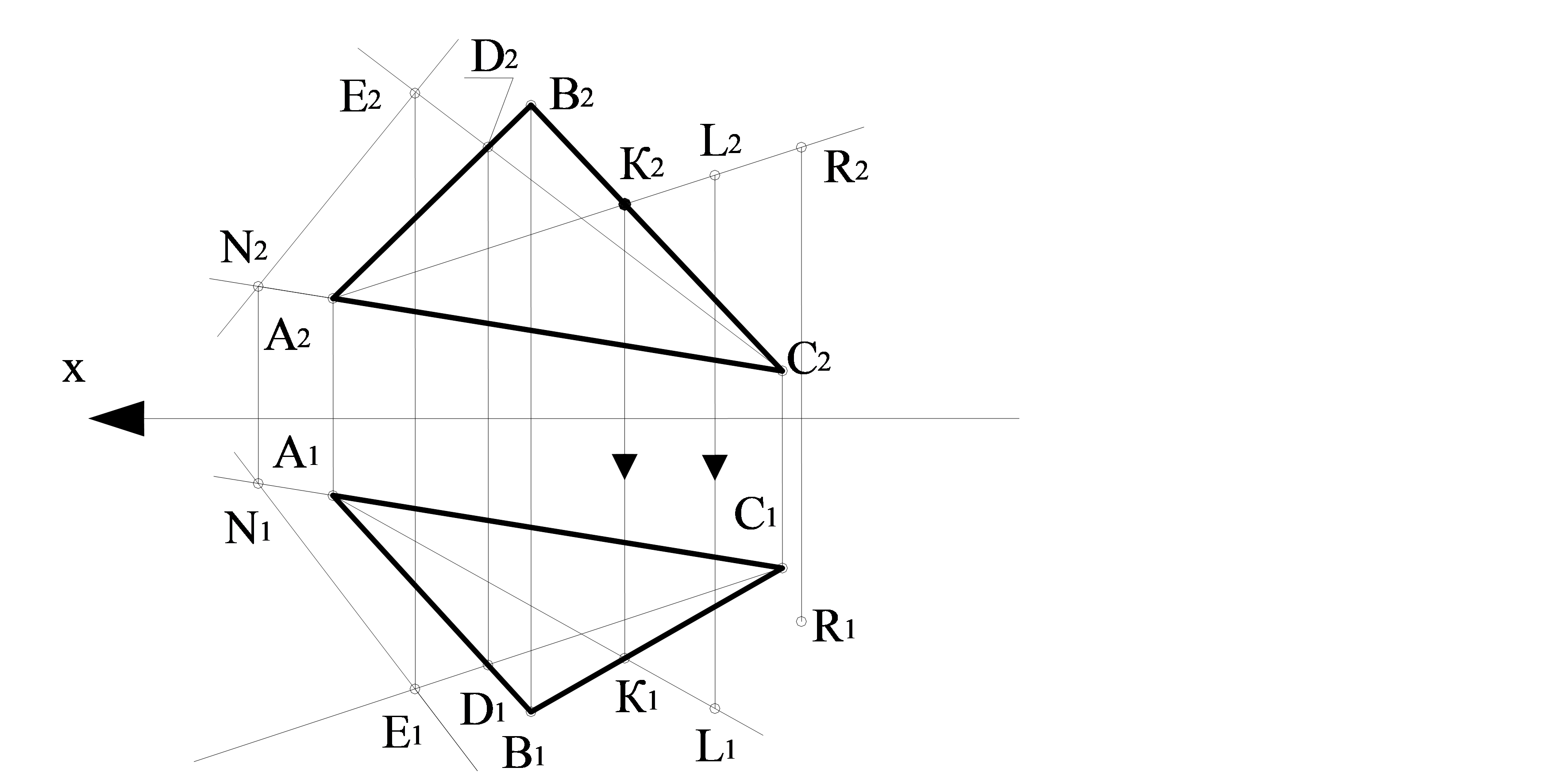
3.5 сурет – жалпы жағдайдағы АВС үшбұрышымен берілген жазықтыққа Ν, Е, L нүктелерінің жататыны
Жазықтықтың денгейлік түзулер деп h горизонталь, f фронталь және р профиль түзулерді атайды. Позициялық, метрлік есептерді шығарғанда жазықтықта жататын денгейлік түзулердің проекцияларын тұрғызу қажет.
Мысал. Π1 проекциясының горизонталь жазықтығына параллель h түзуі жазықтықтың горизонталі деп аталады. H горизонталінің әр нүктесінен горизонталь проекция жазықтығына дейінгі ара қашықтық бірдей, себебі h//π1. Бұл ара қашықтық проекцияның фронталь жазықтығында (z координатты кесінділер түзудің әр нүктесі үшін) бар. Сондықтан горизонтальдің фронталь проекциясы х өсіне параллель, себебі h2//х (3.6а сурет). АВС үшбұрышымен берілген жазықтықта жататын горизонтальдің проекцияларын түрғызу қажет. Біріншіден х өсіне параллель горизонтальдің фронталь проекциясын тұрғызамыз, 12 және 22 қиылысу нүктелерін белгілейміз. Байланыс сызығын қолданып осы нүктелердің горизонталь проекцияларын саламыз. 11 21 нүктелері арқылы өтетің түзу, горизонталь түзудің горизонталь проекциясы.
Мысал. Фронталь проекция жазықтығына параллель келген f түзуі жазықтықтың фронталі деп аталады. Фронтальдің әр нүктесінен фронталь проекция жазықтығына дейінгі ара қашықтығы бірдей. Бұл ара қашықтық горизонталь проекция жазықтығында (у координатты кесінділер түзудің әр нүктесі үшін) бар. Сондықтан фронтальдің горизонталь проекциясы х өсіне параллель, f1//х. (3.6б сурет). АВС үшбұрышымен берілген жазықтықта жататын фронтальдің проекцияларын түрғызу қажет. Біріншіден х өсіне параллель фронтальдің горизонталь проекциясын тұрғызамыз, 11 және 21 қиылысу нүктелерін белгілейміз. Байланыс сызығын қолданып осы нүктелердің фронталь проекцияларын саламыз. 12 22 нүктелері арқылы өтетің түзу, фронталь түзудің фронталь проекциясы.
Профиль проекция жазықтығына параллель келген р түзуі жазықтықтың профиль түзуі деп аталады. Жазықтықтың профиль түзуі ОУ, ОZ өстеріне паралель горизонталь р1 және фронталь р2 проекциялары бар. Ал профиль проекциясын фронталь проекциясындағы 3 және 4 нүктелерін қолданып тұрғызуға болады.
Стр 39 соломонов
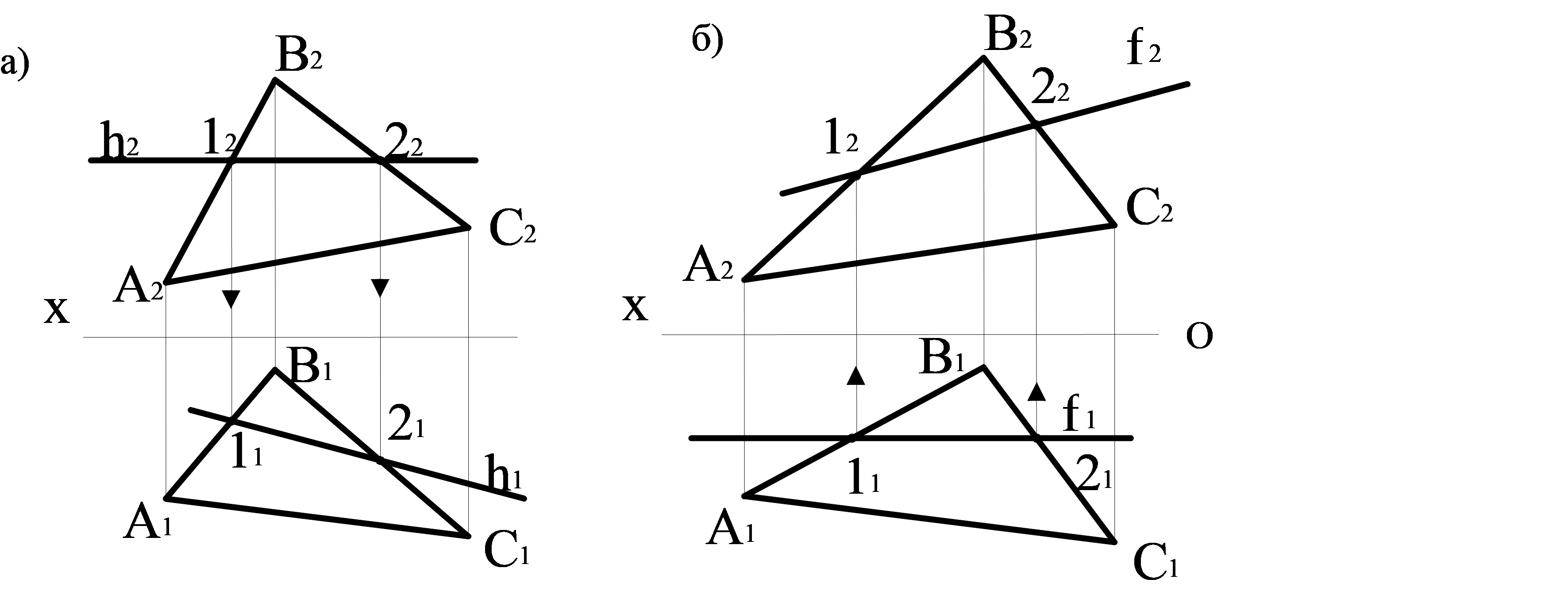
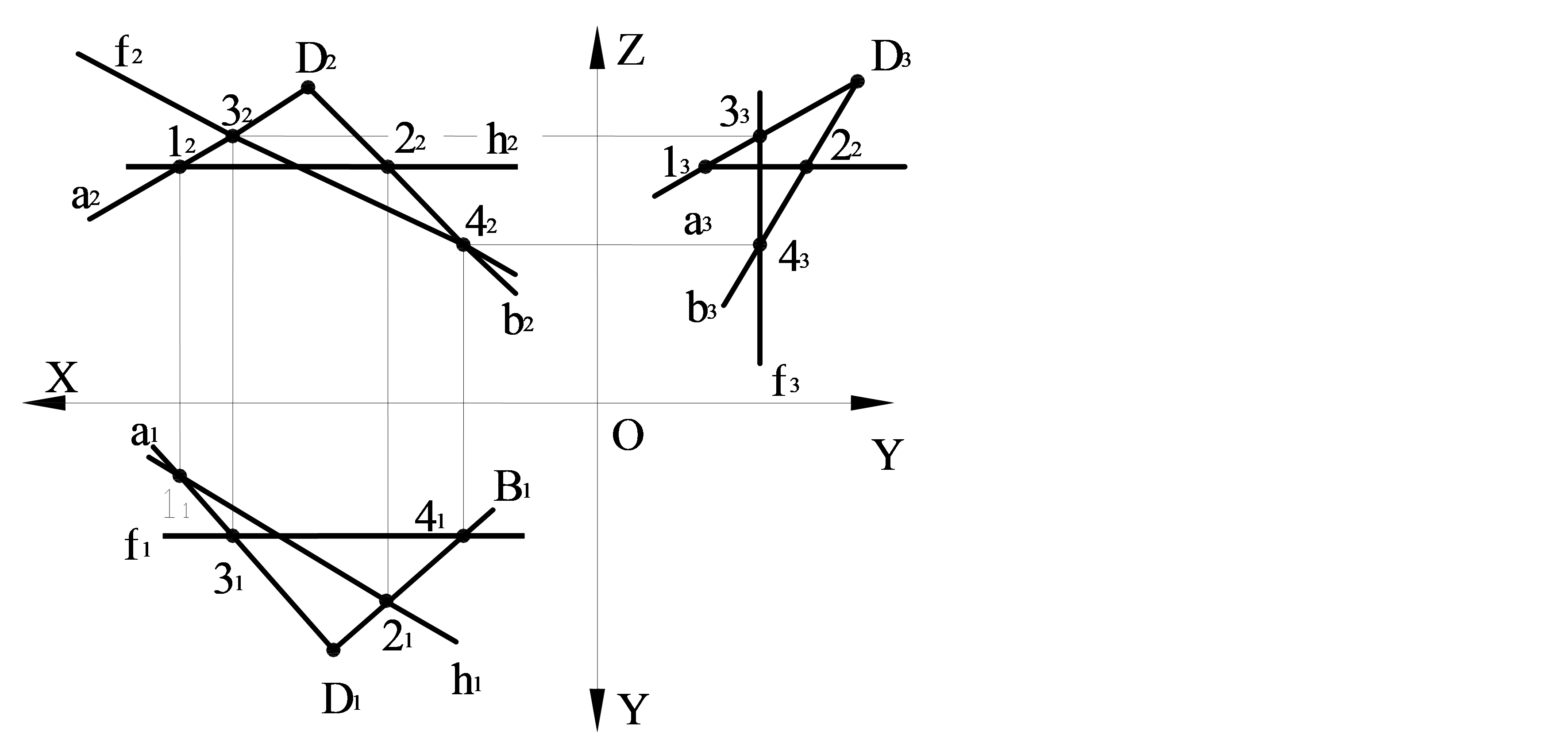
3.6 сурет – Жазықтықтың негізгі сызықтарының проекциялары
а) жазықтықтың горизонталь түзуі; б) жазықтықтың фронталь түзуі; в) жазықтыққа ең үлкен көлбеулі сызығы
Жазықтықта денгейлік түзулер тұрғызғанда ең бастысы бір ереже білу керек: есепті шешу үшін әрдайым осы жазықтықта жататың екі нүкте табылуы қажет.
Жазықтықтың ең үлкен көлбеуінің сызықтары деп жазықтықтың денгейлік сызықтарына перпендикуляр және сол жазықтықта жататын түзулерді атайды.
Мысал. Бірінші жағдайда берілген жазықтықтың горизонталь проекция жазықтығына көлбеуі байқалады, екіншіден – фронталь проекция жазықтығына, үшіншіден – профиль проекция жазықтығына (3.7 сурет). Ең үлкен көлбеулі сызығын (ЕКС) салу оның h1 горизонталь проекциясынан басталады, сондай-ақ тік бұрышты проекциялау қасиетіне сәйкес ЕКС мен h1 арасындағы бұрыш 90º бұрмалаусыз проекцияланады (3.6в сурет). АВС үшбұрышымен берілген жазықтықта жататын горизонтальдің проекцияларын тұрғызу қажет. Біріншіден х өсіне параллель горизонтальдің фронталь проекциясын тұрғызамыз, 12 және 22 қиылысу нүктелерін белгілейміз. Байланыс сызығын қолданып осы нүктелердің горизонталь проекцияларын саламыз, 11 21 нүктелері арқылы өтетін түзу, горизонталь түзудің горизонталь проекциясы болады. Енді осы горизонталь түзудің проекцияларына ең үлкен көлбеулі сызықтарын тұрғызамыз.

3.7 сурет – Жазықтықтың негізгі сызықтарының проекциялары
3.4 Блок. Түзу мен жазықтықтардың өзара орналасуы
Инженерлік сызбаның кейбір тапсырмаларын орындау үшін қарастырып отырған геометриялық нысандардың бір-біріне параллель немесе перпендикуляр орналасуы маңызды орын алады. Осыған байланысты геометриялық нысандардың параллельділігін немесе перпендикулярлығын анықтауға болатын белгілерін, сондай-ақ геометриялық нысандардың бір-біріне белгілі бір бұрышпен орналасқан проекцияларының салу ережелерін қарастырамыз. Бұл белгілер планетария курсынан жақсы белгілі, ал біздің мақсатымыз оларды инженерлік сызба есептерінде қолдану болып табылады.
Егер түзулер өзара параллель болса, онда олардың аттас проекциялары да параллель болады.
Түзу жазықтықта жатқан бір түзуге параллель болса, онда ол осы жазықтықта параллель болғаны.
Мысал. А түзуі жазықтыққа параллель, себебі ол π1 жазықтықта жатқан b түзуіне параллель (3.8 сурет).
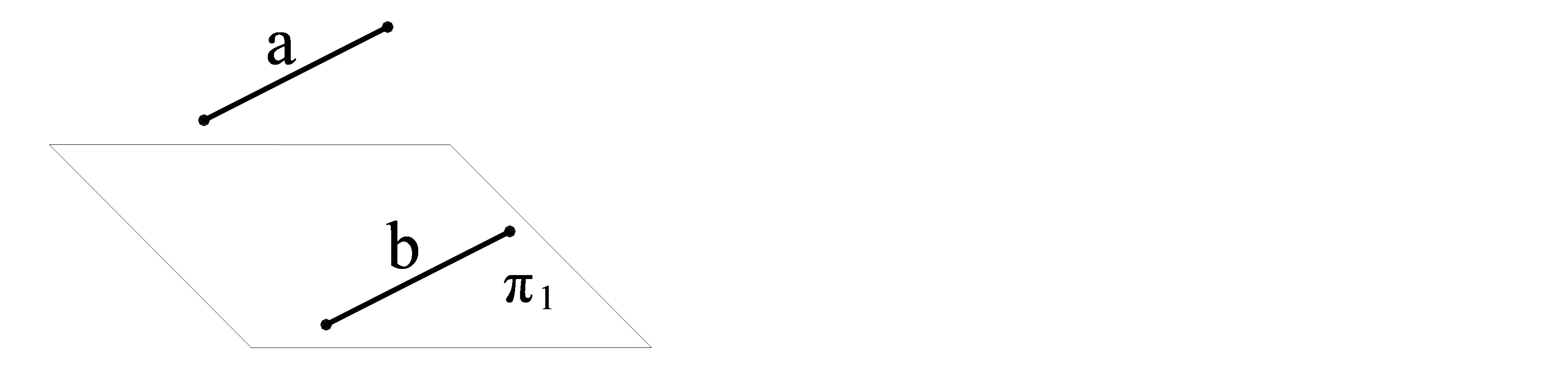
3.8 сурет – π1 жазықтығына параллель а түзудің проекциясы
Кеңістіктің берілген нүктесі арқылы өтетін түзуді салу үшін параллель берілген жазықтыққа осы жазықтықта жатқан кез келген түзуге параллель түзуді жүргізу жеткілікті. Осыған байланысты көп шешімдер болуы мүмкін. Параллель түзуді салу үшін осы жазықтықта жатқан аттас түзудің проекциясына (мысалы, DЕ) оның екі проекциясы да параллель болу керек (3.9 сурет).
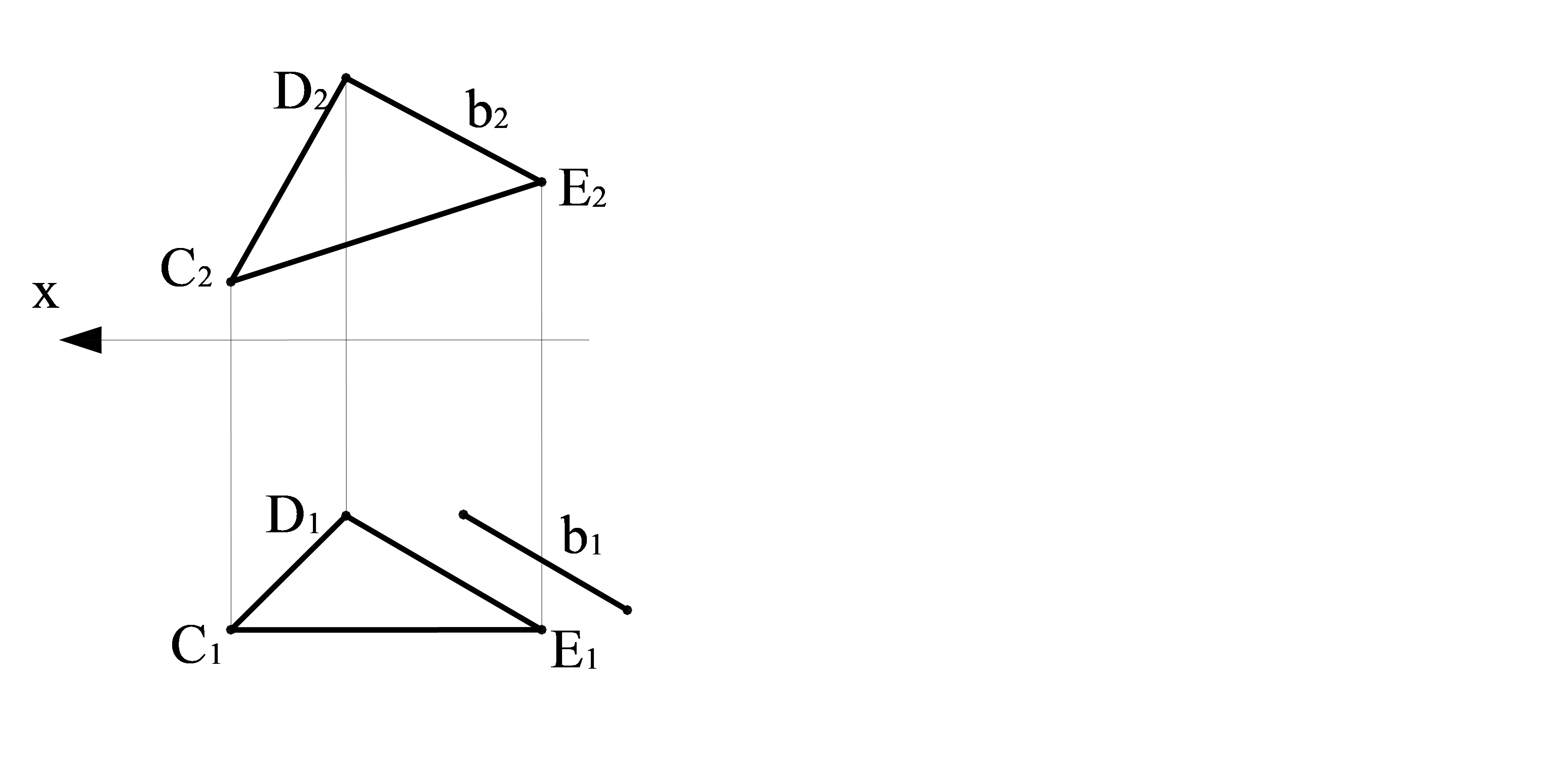
3.9 сурет – СЕD жазықтығына параллель b түзуін тұрғызу
Жазықтықтар бір-біріне параллель болады, егерде бір жазықтықтың қиылысатын екі түзуі басқа жазықтықтың қиылысатын екі түзуіне параллель болса.
Мысал. Берілген жазықтықтардың өзара параллель екенін тексеру үшін, сол берілген жазықтықтардың қиылысқанын түзулерінін көрінісін тексеру қажет. Ұсынылған СВD және АЕF жазықтықтардың қиылысқан түзулері өз-ара параллель екен (СВ//АЕ және ВD//ЕF), сол себептен жазықтықтар бір-біріне параллель (3.10 сурет).
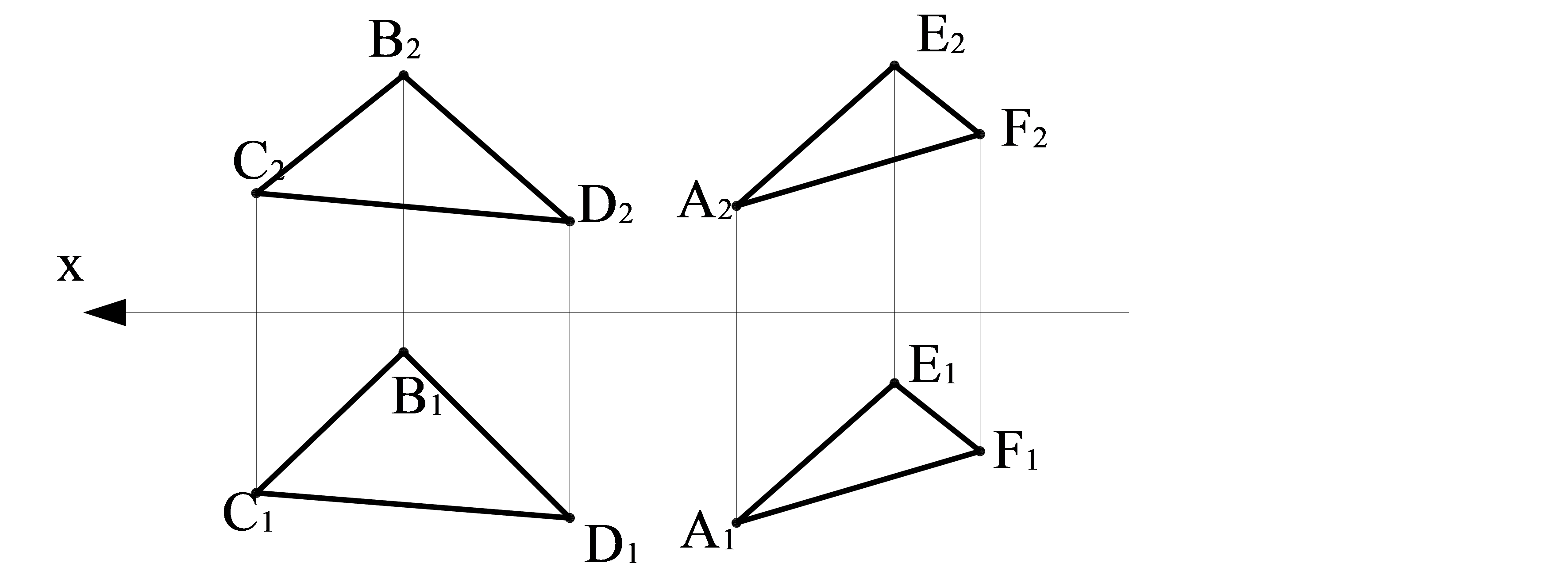
3.10 сурет – Өзара параллель СDD және AEF жазықтықтары
3.4.1 Блок. Түзу мен жазықтықтардың перпендикулярлығы
Геометриялық нысандардың перпендикулярлығы тұрғызуын түзу мен жазықтықтың перпендикулярлығын қарастырудан бастаймыз, себебі қалған нұсқалар осы белгісіне байланысты.
Егерде түзу жазықтықта жатқан екі қиылысатын түзулерге біріншісі фронталь, екіншісі горизонталь перпендикуляр болса, онда түзу жазықтыққа перпендикуляр болғаны.
Жазықтыққа перпендикуляр салу кезінде горизонталь және фронталь таңдап алынады. Осы жағдайда, кешенді сызбада тік бұрышты проекциялау қасиетін пайдаланып, перпендикулярдың фронталь проекциясын фронтальдің фронталь прекциясына 90° бұрышпен, ал перпендикулярдың горизонталь проекциясын – горизонтальдің горизонталь проекциясына 90° бұрышпен жүргіземіз.
Мысал. D нүктесінен өтетін АВС жазықтығына перпендикуляр тұрғызу қажет (3.11 сурет).
Алдымен жазықтықтың негізгі (горизонталь және фронталь) сызықтарын саламыз – содан соң D1 нүктесінен h1 түзуіне перпендикуляр жүргіземіз, ал D2 нүктесінен – f2 түзуіне перпендикуляр.
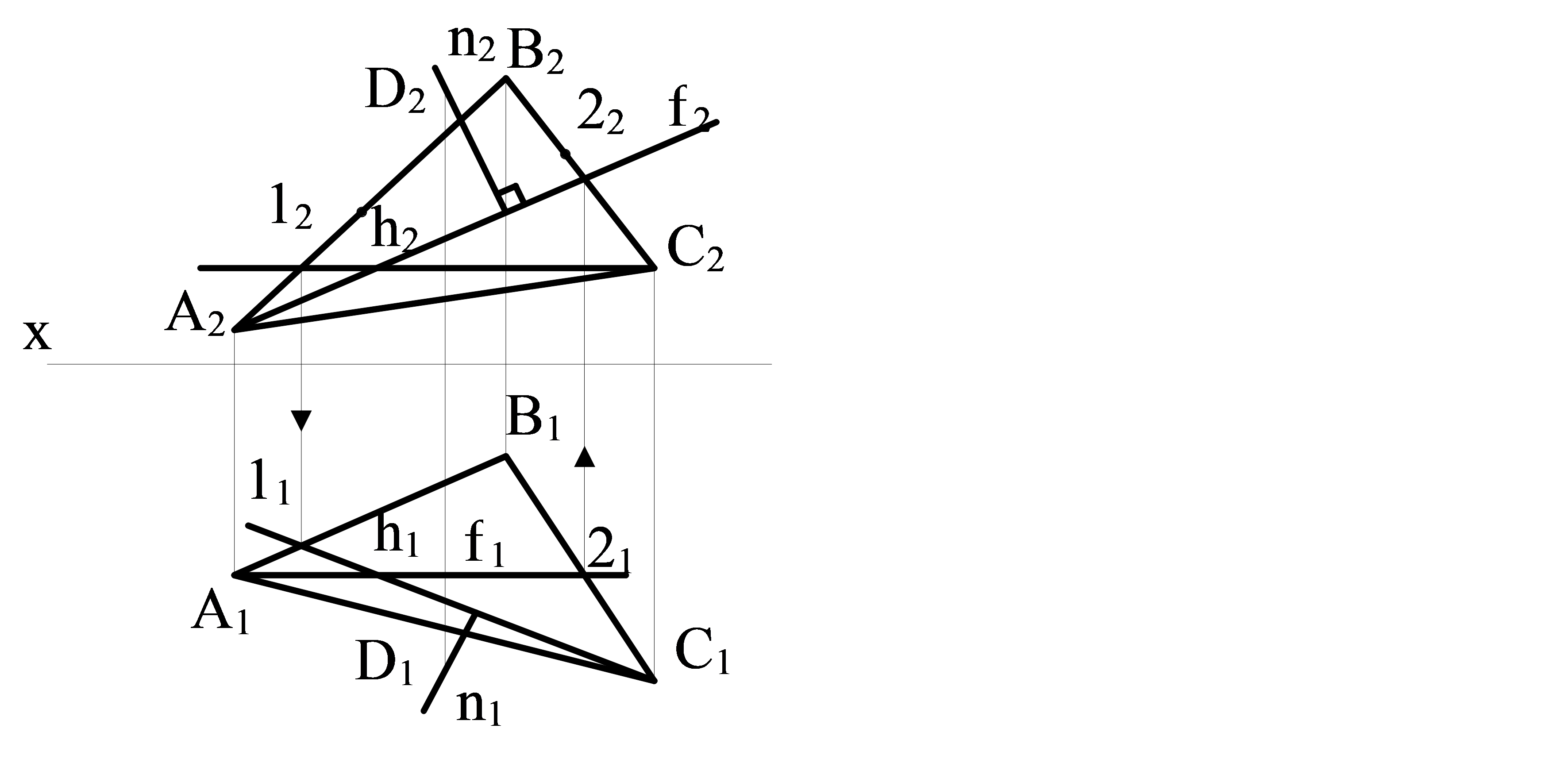
3.11 сурет – D нүктесінен АВС жазықтығына жүргізілген перпендикулярдың проекциясы
Түзулер өзара перпендикуляр болады, егер олардың біреуіне басқа түзуге перпендикуляр болатын жазықтықты тұрғызу мүмкін болса.
Мысал. В нүктесінен өтетін d түзуіне перпендикуляр тұрғызу қажет (3.12 сурет). Біріншіден В нүктесінен өтетін d түзуіне перпендикуляр тұрғызамыз. Бұл жазықтық f фронталь және h горизонтальмен беріледі, бұл жерде горизонтальдің горизонталь проекцясы d түзуінің горизонталь проекциясына перпендикуляр, ал фронтальдің фронталь проекциясы d түзуінің фронталь проекциясына перпендикуляр болады. Горизонтальдің фронталь проекциясын және фронтальдің горизонталь проекциясын ОХ өсіне параллель тұрғызамыз. Осы жазықтықта жатқан кез келген түзу d түзуіне перпендикуляр болады, мысалы ВС түзуіне.
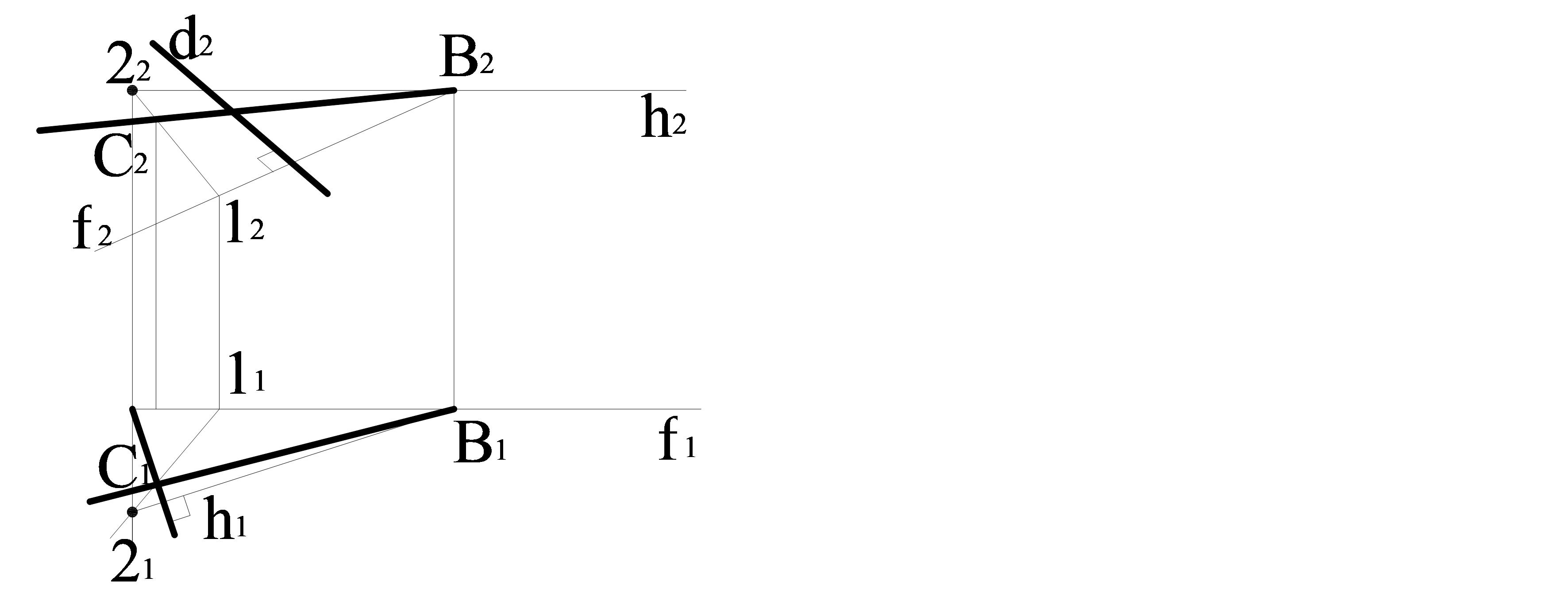
3.12 сурет – d және ВС өзара перпендикуляр түзулерді түрғызу
Екі жазықтық бір – біріне перпендикуляр болады, егерде олардың біреуі жазықтыққа перпендикуляр жүргізілген түзу арқылы өтетін болса.
Мысал. Кеңістікте үшбұрышпен берілген АВС жазықтығына L түзуі арқылы берілген жазықтыққа перпендикуляр тұрғызу қажет (3.13 сурет). Біріншіден L түзуі арқылы берілген жазықтықта К нүктесін табамыз. АВС үшбұрышымен берілген жазықтықта біріншіден f фронтальлін және h горизонтальлін тұрғызамыз. Бұл жерде L түзуінің К нүктесінен ерікті n түзуін тұрғызамыз. N түзуі ерікті жүргізіледі. N1 түзуі горизонтальдің горизонталь проекциясына, ал n2 түзуі фронтальдің фронталь проекциясына перпендикуляр тұрғызылады.
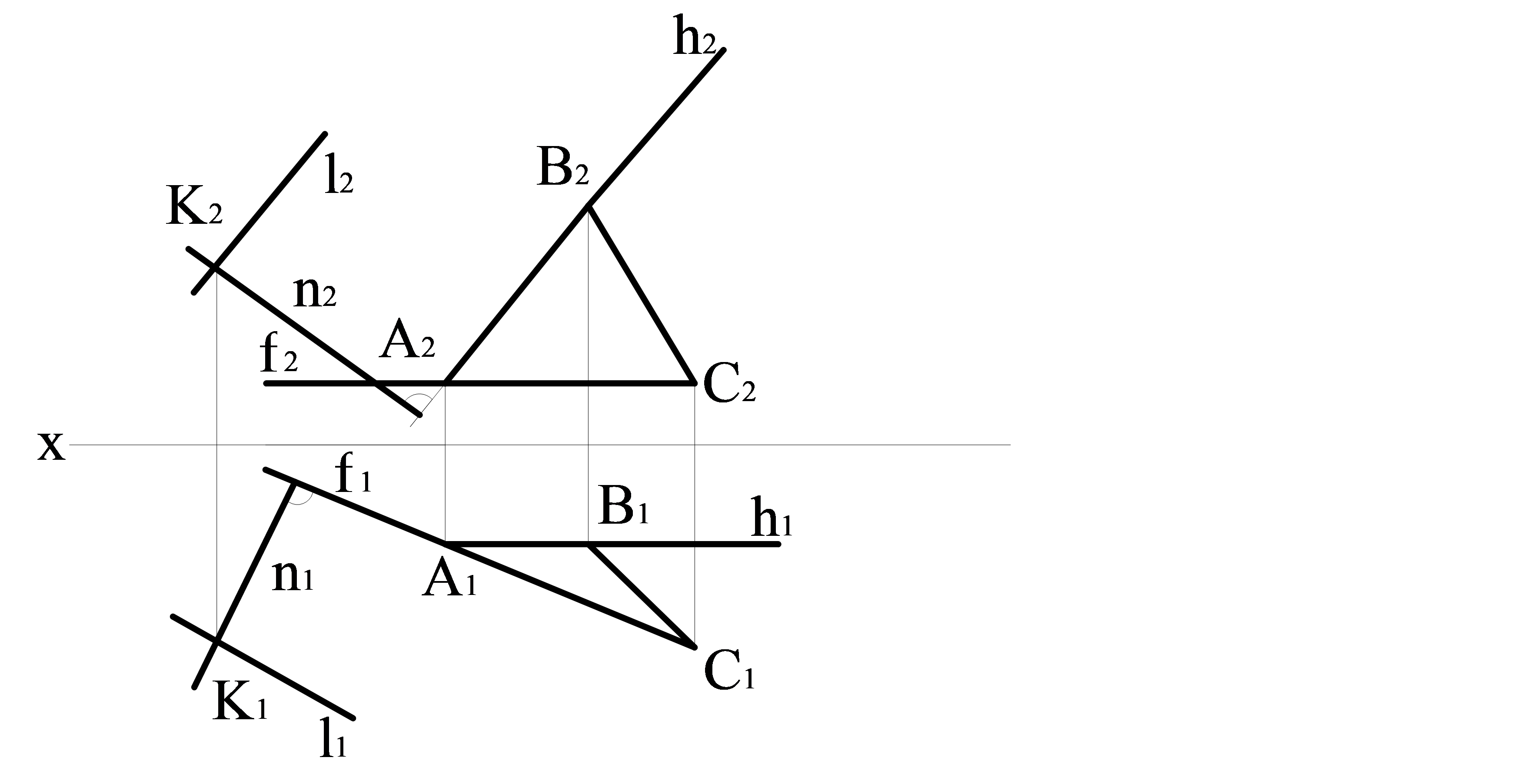
3.13 сурет – Өзара перпендикуляр жазықтықтардың көрінісі
3.5 Блок. Жазықтықтағы позициялық есептер
Фигуралардың қандай-да бір жалпы элементтерін анықтауға арналған есептер позициялық есептер деп аталады, мысалы түзу мен жазықтықтың қиылысу нүктелері, екі жазықтықтың қиылысу сызықтары.
3.5.1 Блок. Түзу мен жазықтықтың қиылысуы
Түзу мен жазықтықтың қиылысуына арналған есептерді қосымша қиылысатын жазықтықтың көмегімен шығаруға болады, ол жазықтық келесі шарттарды қанағаттандыруы керек:
- жазықтық дербес жағдайдағы жазықтық болуы керек, себебі дербес жағдайдағы жазықтық сәйкес проекция жазықтығына түзу түрінде проекцияланады;
- іздеп отырған жазықтықпен қиылысу нүктесі және түзуі арқылы өтуі қажет.
Мысал. Кеңістікте жазықтық дербес жағдайдағы берілген. Ол – горизонталь проекциялаушы АСD үшбұрышымен берілген (3.14 сурет). Оның d түзуімен қиылысу нүктелерін табу керек. Горизонталь проекциялаушы жазықтық горизонталь проекция жазықтығына түзуге айналғандықтан, нүктенің горизонталь проекциясы Е1 болады. Әрі қарай байланыс сызығын қолданып d2 түзуінде қиылысу Е2 нүктесінің фронталь проекциясын табамыз. D түзуінің көрінетін бөліктерін анықтау қажет, себебі фронталь проекция жазықтығында көрсетілген түзудің бөлігі бақылаушыдан АСD үшбұрыш жазықтығымен көрінбейтін. Ол үшін АСD үшбұрыш жазықтығында жататын қандай да бір түзуімен, мысалы AD түзуімен және де d түзуінің фронталь проекцияларының қиылысу нүктесін қарастыру керек. Бұл нүктені 12 деп белгілейміз. Бірақ d түзуі және АСD үшбұрыш жазықтығы тек бір ғана нүктеде қиылыса алады, біз оны Е2 деп таптық. Демек, d және АС түзулері кеңістікте қиылысады. Онда олардың проекцияларының қиылысатын барлық нүктелері бәсекелес болады, дәлірек айтқанда 12 мен 22. Онда горизонталь проекция жазықтығында байланыс сызығы бойынша 11 нүктесі А1С1 және 21 нүктесі d1 қиылысады. D түзуінде жататын 2 нүктесі көрінетін болып табылады. Бұл Е2 қиылысу нүктесіне дейін орындалады. D түзуінің бөлігі АВС үшбұрыш жазықтығының астынан шыққанға дейін көрінбейтін болады.
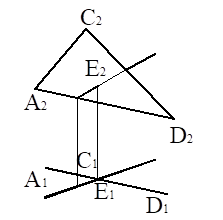
3.14 сурет – Горизонталь проекциялаушы АСD жазықтығымен d түзуінің қиылысуы
Мысал. Жалпы жағдайдағы ADF жазықтығы мен d түзуінің қиылысу нүктелерін табу қажет (3.15 сурет). D түзуі арқылы дербес жағдайдағы жазықтықты салу керек (мысалы, фронталь-проекциялаушы). Осы жазықтықтың қиылысу сызығы фронталь проекция жазықтығында d түзуімен сәйкес келеді, η2 = d2. Онда 32 және 42 қиылысу нүктелері бойынша 31 және 41 нүктелерін саламыз, содан соң η жазықтығы мен ADF жазықтықтарының қиылысу сызықтарының горизонталь проекциясы болатын 31 және 41 түзулерін саламыз. Сондай-ақ 3 пен 4 түзуі ADF жазықтығын қияды, онда Е1 нүктесі d түзуі мен ADF жазықтығының қиылысу нүктесінің горизонталь проекциясы болады. Ол арқылы Е2 фронталь проекциясын табамыз, ол d2 түзуінде жатуы керек (өйткені қиылысу нүктесі d түзуіне де және ADF жазықтығына да жатады). Бәсекелес нүктелері бойынша d түзуінің екі проекциясында көрінетін бөліктерін анықтаймыз. Фронталь проекция жазықтығында көрінетін жерлерін анықтау үшін фронталь-бәсекелес нүктелерін (мысалы, 32=52 нүктелері, мұнда d түзуі мен ADF жазықтығы қиылысады) анықтаймыз. Көріп отырғандай, фронталь проекция жазықтығында 32 нүктесінен жоғары, онда осы нүктеде А2D2 жоғары, ал d2 түзуі оның астында болады. Ол тек Е2 қиылысу нүктесіне дейін ғана дұрыс. Содан соң d2 жоғары болады. Дәл осындай түрде горизонталь-бәсекелес нүктелері арқылы (мысалы, 61=71) 61=71 нүктелеріндегі D1F1 түзуі d1 түзуіне қарағанда жоғары жатыр, себебі 72 нүктесі 62 нүктеге қарағанда жоғары. D түзуінің көрінбейтін бөліктерін үзік сызықтармен белгілейміз.

3.15 сурет – d түзуі мен АВС үшбұрыш жазықтығының қиылысу нүктелері
3.5.2 Блок. Жазықтықтардың қиылысуы
Екі жазықтықтың қиылысу түзуі екі жазықтықта да жататын екі нүктемен анықталады. Бұл жерде негізгі міндет екі жазықтық үшін ортақ нүктелерді табу болып табылады. Екі жазықтықтардың қиылысу есебі екінші позициялық есептер деп аталады.
Берілген есептерді шешу үшін көмекші қиюшы жазықтықтар әдісі пайдаланылады. Жазықтықтарды қиятын көмекші қиюшы жазықтықтар енгізіледі. Әрбір көмекші қиюшы жазықтық үшін берілген жазықтықтармен оның қиылысу сызығын саламыз. Пайда болған екі сызықтың қиылысу нүктесі берілген жазықтықтардың да қиылысу нүктесі болады. Көмекші қиюшы жазықтықтар екеу болғандықтан, берілген жазықтықтың қиылысу нүктесі де екеу болады. Әрине, әрбір көмекші қиюшы жазықтық кеңістікте дербес жағдайда болуы керек, онда көмекші қиюшы жазықтық перпендикуляр болатын жазықтық проекциясына ол түзу болып проекцияланады. Әйтпесе, егер көмекші қиюшы жазықтық жалпы жағдайда орын алса, онда көмекші қосымша жазықтықты енгізу есептің шығарылуын жеңілдетпейді.
Мысал. Өзара параллель түзулермен берілген (а//b) Q жазықтықтығы мен Σ(ΔCDE) жазықтықтығының қиылысу сызығын табу қажет (3.15сурет).
Жазықтықтың қиылысу сызығының проекцияларын табу үшін көмекші қиюшы жазықтықтарды бір проекция жазықтығына препендикуляр тұрғызамыз. Жазықтықтардың фронталь проекцияларын қиып өтетін P(P2) фронталь-проекциялаушы жазықтықты тұрғызып нүктелерін табамыз. 12,22,32,42 – Σ2,Q2 және P жазықтықтарының қиылысу нүктелері. Енді осы 12,22,32,42 нүктелерінен проекциялық байланыс сызықтарын жүргізіп 11,21,31,41 горизонталь проекцияларын табамыз да оларды бастыра түзу жүргіземіз. Берілген жазықтықтардың P(P2) қосымша жазықтықтармен қиылысу сызығының горизонталь проекциясы N1 нүктесін береді. Енді N1 нүктесінің проекциялық байланыс сызықтарын жүргізіп фронталь проекциясын табамыз. Жазықтықтырдың фронталь проекцияларын қиып өтетін L(L2) фронталь-проекциялаушы жазықтықты тұрғызып нүктелерін табамыз. 52, 62, 72, 82 – Σ2, Q2 және L2 жазықтарының қиылысу нүктелері. Енді осы 52,62,72,82 нүктелерінен проекциялық байланыс сызықтарын жүргізіп, 51, 61, 71, 81 горизонталь проекцияларын табамыз да, оларды бастыра түзу жүргіземіз. Берілген жазықтықтардың L(L2) қосымша жазықтықтармен қиылысу сызығының горизонталь проекциясы К1 нүктесін береді. Енді К1 нүктесінің проекциялық байланыс сызықтарын жүргізіп фронталь проекциясын табамыз.
N1 мен К1 және N2 мен К2 қосқанда NК түзуі пайда болады: NК түзуі Q(а//b) мен Σ(ΔCDE) жазықтықтарының өзара қиылысуы.

3.16 сурет – Σ(ΔCDE) және Q(а//b) жазықтықтардың қиылысу сызығы
Мысал. Үшбұрыштармен берілген екі жалпы жағдайдағы жазықтықтардың қиылысу сызығының проекцияларын салып, көрінетін бөліктерін анықтау қажет (3.17 сурет).
Жазықтықтардың қиылысу сызығын тұрғызу үшін көмекші қиюшы жазықтықтар енгізу тәсілін қолданамыз. Есепті шешуді жеңілдету үшін қиюшы жазықтықтарды үшбұрыштардың қабырғаларынан өткіземіз. Үшбұрыштың DF қабырғасы арқылы көмекші фронталь проекциялаушы L жазықтығын жүргіземіз. L1 = D1F1, ол Δ АСЕ және Δ DFК жазықтықтарының қиылысу сызығының горизонталь проекциясы. Проекциялық байланыс сызығын жүргізіп оның горизонталь проекциясын табамыз. Δ DFК жазықтығында D2F2 сызығы болады. Δ АСЕ үшін қиылысу нүктелерінің 11,21 горизонталь проекциялары арқылы проекциялық байланыс сызығын пайдаланып, олардың 12 және 22 фронталь проекцияларын табамыз. 12 және 22 қиылысу нүктелерін қосып L және Δ DFК жазықтықтарының қиылысқан сызықтарын табамыз. D2 F2 және 12 және 22 сызықтарды ұзартып, олардың N2 қиылысу сызғын табамыз, осы нүкте берілген жазықтықтардың қиылысқан нүктесі болып табылады. N2 нүктесі үшбұрыштарға жатпайды, сол себептен үшбұрыштардың қиылысу нүктесі емес, үшбұрыштар жатқан жазықтықтың қиылысу нүктесі болып саналады. Енді, екінші Δ АСЕ жазықтығының СЕ қырынан өтетін L көмекші горизонталь-проекциялаушы жазықтық енгізіп, ұсынылған ұшбұрыштардың қиылысқан нүктесі M2 нүктесін табамыз.
N2 және M2 нүктелерін тоғыстырып, ΔАСЕ және ΔDFК жазықтықтарының қиылысу сызығының фронталь проекциясын табамыз. Қиылысу сызығының фронталь проекциясынан проекциялық байланыс сызығын пайдаланып, ΔАСЕ және ΔDFК жазықтықтарының қиылысу сызығының горизонталь проекциясын табамыз. Үшбұрыштардың көрінетін бөліктері бәсекелес нүктелердің көмегімен анықталады. 21 және 31 нүктелері табылған. Егерде нүктелердің фронталь проекцияларына қарасақ, 21 көрінбейді. Демек, осы нүктеде Д1С1 түзуі С1F1 түзуінен биік, себебі үшбұрышпен берілген жазықтық А1 С1 F1 еш жерде қиылыспайды. Сонда N1M1 басқа жағынан D1F1К1 үшбұрыш жазықтығы төмен болады. Осыған
ұқсас фронталь проекциясында да айқас DF және АС түзулерінде бәсекелес 5 және 6 нүктелерінің көріністерін табамыз. Үшбұрыштардың көрінетін қабырғаларын негізгі тұтас сызықпен бастыра жүргізіп, көрінбейтін бөлігін үзік сызығымен кескіндейді.
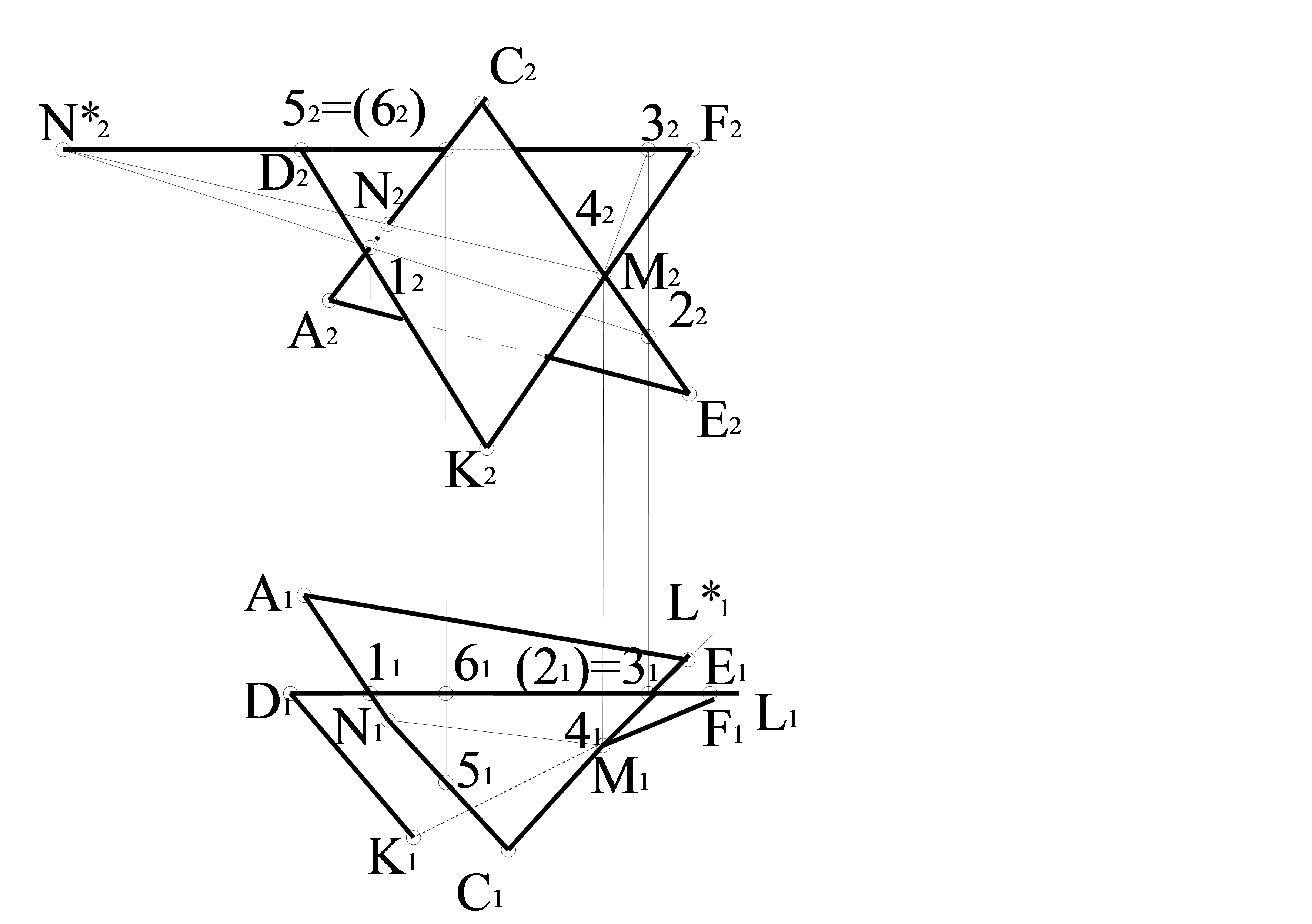
3.17сурет – Үшбұрыштармен берілген жалпы жағдайдағы екі жазықтықтың қиылысу сызығы
3.5.3 Блок. Жазықтықтардың іздері
Берілген жазықтықтың басқа проекция жазықтығымен қиылысуының түзу сызығы жазықтықтың ізі деп аталады. Горизонталь проекция жазықтығымен жазықтықтың қиылысуы горизонталь ізін, ал фронталь проекция жазықтығымен жазықтықтың қиылысуы фронталь ізін береді. Фронталь іздің фронталь проекциясы горизонталь іздің горизонталь проекциясы сияқты іздің өзімен сәйкес келеді, ал фронталь іздің горизонталь проекциясы және горизонталь іздің фронталь проекциясы ОХ өсінде жатады.
Мысал. ADC үшбұрышымен берілген жазықтық іздерін табу қажет (3.18 сурет). Есептерді шешу үшін үшбұрышпен берілген ADC жазықтығында екі түзуді таңдап және олардың горизонталь проекция және фронталь проекция жазықтықтарымен қиылысу нүктелерін, яғни горизонталь және фронталь іздерін табу жеткілікті.
Бұл нүктелерді горизонталь проекция және фронталь проекция жазықтықтарымен тоғыстырып жазықтықтың іздерін табамыз. Дәлілек қарастырсақ, ΔADC жазықтығында жатқан CD мен DC түзулерін таңдаймыз. Біріншіден CD түзуі үшін шешімін аламыз. C2D2 түзуін ОХ өсімен қиылысуына дейін созып, М2 горизонталь ізінің фронталь проекциясын аламыз.
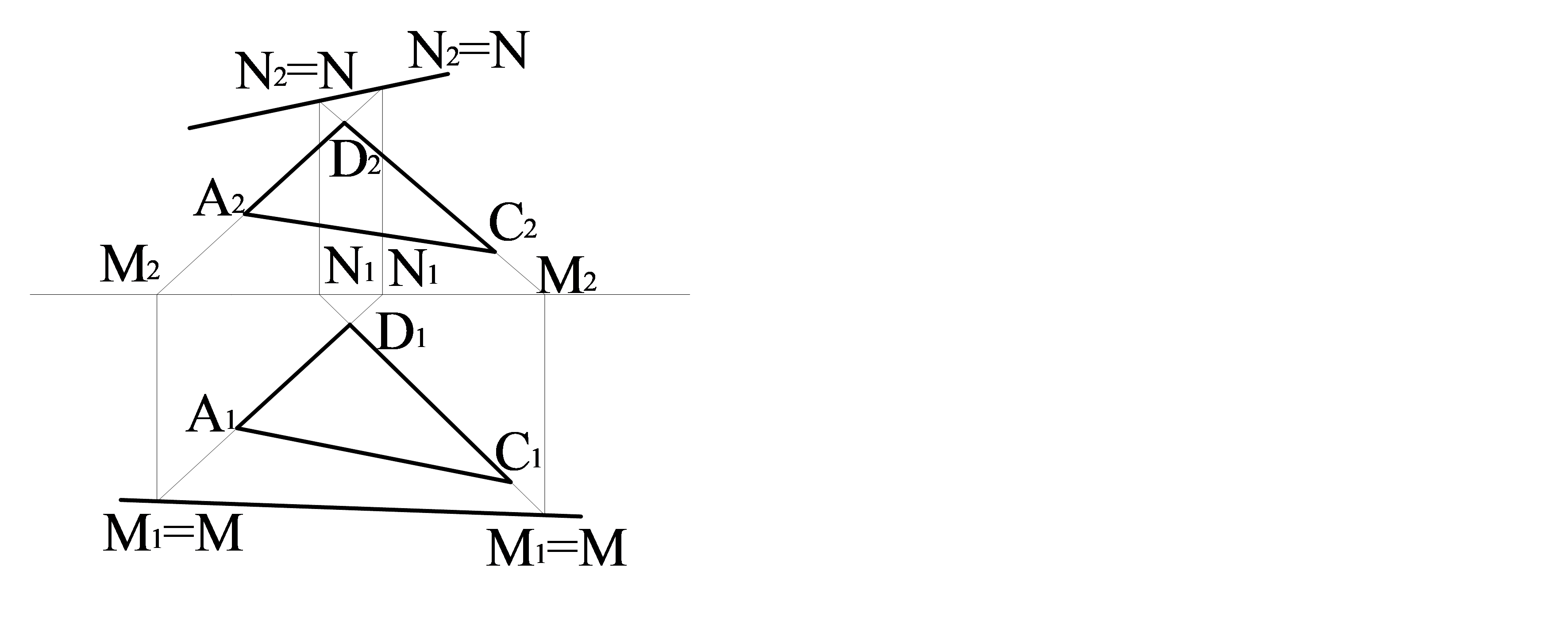
3.18 сурет – Δ ADC жазықтықтың іздері
Тік түзу мен C1D1 түзудің жалғасуының қиылысуы М нүктесі горизонталь ізі болып табылады. Фронталь ізін табу үшін C1 D1 түзуін ОХ өсімен қиылысуына дейін жалғастырамыз, мұнда N1 фронталь ізінің горизонталь проекциясы жатыр. Осы нүктеден C2D2 кесінді жалғасуымен қиылысуына дейін тік түзуді жүргіземіз. Осында N фронталь ізін табамыз. DC түзуін тұрғызуды аналогиялық түрінде жүргіземіз, М горизонталь және N фронталь іздерін саламыз. Аттас N және N1, М және М1 іздерді тоғыстырып, ΔADC жазықтығының горизонталь және фронталь іздерін табамыз.
Ұсынылған теориялар төмендегі жағдайларға негізделеді:
1) жазықтық кеңістікте берілуі мүмкін:
- бір түзуде жатпайтын үш нүктемен;
- түзу және осы түзуге жатпайтын нүктемен;
- екі параллель түзумен;
- екі қиылысатын түзумен;
- жазық фигурамен;
- ізбен.
2) кеңістіктегі жазықтық тапсырмасына көрсетілген нысандары (нүкте, түзу, фигура) проекциямен берілген кешенді сызбалар сәйкес келеді;
3) егер түзудің екі нүктесі жазықтықта жатса, онда түзу де жазықтықта жатады;
4) егер нүкте жазықтықта жатса, онда ол осы жазықтықта жатқан кез келген түзуге жатады;
5) ортогоналды проекцияларды салу әдісін пайдаланып, нүкте, түзу, бір-біріне және проекция жазықтығына қатысты жазықтықтардың өзара орналасуын анықтайтын позициялық есептердің шексіз жиынын шығаруға болады;
6) кеңістікте түзу мен жазықтық мүмкін: ортақ нүктелері болмауы, тек бір ғана ортақ нүктеге ие болуы, көптеген ортақ нүктелерге ие болуы. Осыған байланысты түзу жазықтықта жатуы, оған параллель, осы жазықтықпен қиылысуы, кейбір уақытта оған перпендикуляр болуы мүмкін;
7) екі жазықтық кеңістікте бір-біріне параллель, бір-бірімен қиылысуы, және жекелеген жағдайда өзара перпендикуляр болуы мүмкін;
8) Екі қиылысушы жазықтықтар бір ортақ түзуге – қиылысу сызығына ие;
9) Жазықтықты қиятын түзу онымен бір ортақ нүктеге ие;
10) Жазықтыққа перпендикуляр тұрғызу үшін тік бұрышты проекциялау қасиеттерін қолдану қажет.
Тапсырмалар:
1 есеп. С(25; 15; 5), D(60; 45; 25), E(30; 5; 60) төбелерінің координаттары бойынша үшбұрышытың эпюрасын тұрғызыңыз.
2 есеп. Δ АВС жазықтығы берілген. Жазықтыққа К нүктесінен өтетін перпендикуляр тұрғызу қажет (3.19 сурет).
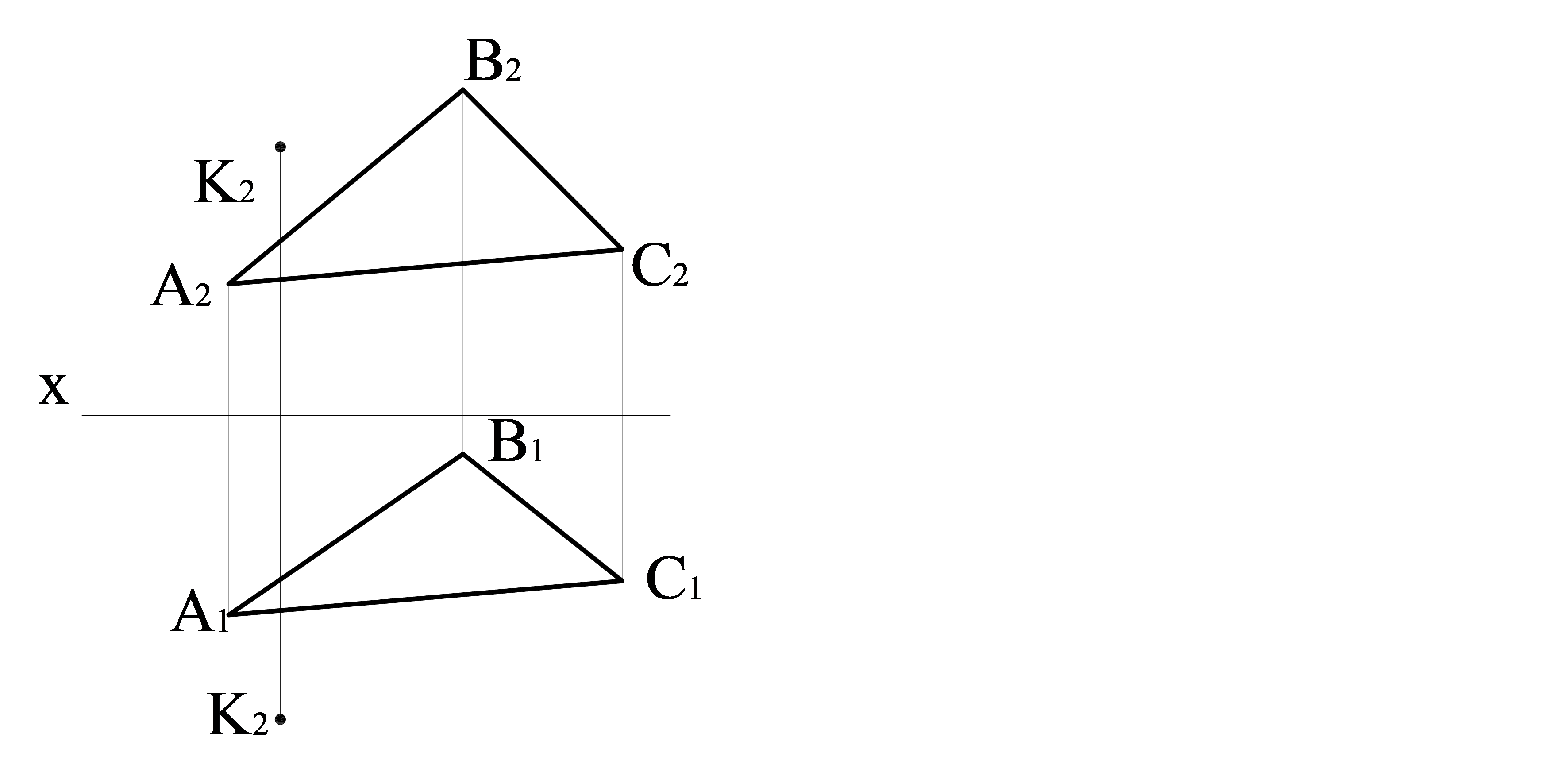
3.19 сурет
Өзіндік талдау үшін сұрақтар:
1) Жазықтықты берудің қандай әдістері белгілі?
2) Жазықтық қалай аталады, егер ол:
- қандай да бір жазықтық проекциясына параллель;
- қандай да бір жазықтық проекциясына перпендикуляр.
3) Жазықтық сызығына жататынды қандай шарт анықтайды?
4) Жазықтықтың негізгі сызықтарын атаңыз.
5) Нүкте жазықтықта жататындардың шарттары қалай?
6) Проекцияланатын жазықтық пен деңгей жазықтығының салыстырмалы талдауын жасаңыз.
7) Горизонталь, фронталь және профиль түзу проекцияларының ұқсастықтары мен айырмашылықтарын анықтаңыз.
8) Түзу мен жазықтықтың және екі жазықтықтың параллельділігінің белгілерін атаңыз.
9) Қандай түзу жалпы жағдайдағы жазықтықтың фронталь проекция жазықтығымен қиылысуының сызығы болып табылады?
10) Қандай сызық бойынша екі горизонталь проекция жазықтығы қиылысады?
11) Екі жазықтықтың және түзу мен жазықтықтың қиылысуы кезіндегі қалай анықталады?
12) Түзу мен жазықтықтың қиылысу нүктелерін салу реттілігі қандай?
13) Берілген жазықтыққа перпендикуляр түзуді қалай салуға болады?
14) Жалпы жағдайдағы түзуге перпендикулярды қалай жүргізуге болады?
15) Берілген жазықтыққа перпендикуляр жазықтықты түзу арқылы қалай жүргізеді?
16) Биссектор жазықтығы деп қандай жазықтықты атайды?
17) Жазықтықтың ең үлкен көлбеуінің сызықтары деп нені айтады?
18) Жазықтықтың іздері деген не?
Бақылау тапсырмалары:
Есеп 1. Д нүктесінен АВС үшбұрышымен берілген жазықтыққа перпендикуляр түсіру қажет: А (45,170,60); В (15,20,30); С (80,45,10); Д (80,20,90).
Есеп 2. АВ және СД қиылысатын түзулерімен берілген жазықтықта ең үлкен көлбеу сызығын тұрғызу қажет (3.20 сурет).

3.20 сурет
Әдебиеттер
Негізгі:
1 Есмуханов Ж. М. Сызба геометриясы есептері. – Алматы: Білім,1995. – 272 б.
2 Ақпанбек Ғ. Сызба геометрия. – Алматы,1998. – 208б.
3 Ақпанбеков Ғ. Сызба геометрия. – Алматы: «Қазақ универсиверситеті», 1992. – 120 б.
4 Миронова Р.С., Миронов Б.Г. Сборник заданий по черчению. – М.: Высшая школа, 2004. – 355 с.
Қосымша
5 Чекмарев А.А. Инженерная графика. – М.: Высшая школа, 1988. – 365с.
6 Короев Ю.И.Черчение для строителей. – М.: Стройиздат, 2001. – 256 с.
7 Крылов Н.Н. Начертательная геометрия. – М.: Высшая школа, 2005. – 224 с.