Модуль. Проекциялар әдісі. Нүктенің проекциясы
1.1 Блок. Орталық және параллель проекциялау
Орталық проекция әдісі бойынша жазықтықтарға нысандарды бейнелеу механизмі 1.1 а суретінде көрсетілген. Орталық проекция құралы ретінде қолданылады: π – проекция жазықтығы; С, Е, D – геометриялық нүктелер нысандар; S – проекция центрі; Сπ, Еπ, Dπ – С, Е, D нүктелерінің π жазықтығындағы орталық проекциялары. Орталық проекцияның басты белгілері:
- кеңістіктегі әрбір нүктеге бір ғана проекция сәйкес келеді;
- әр проекцияға кеңістіктегі проекцияланатын түзуде жататын көптеген нүктелер сәйкес келеді;
- 3) проекцияланатын түзумен сәйкес келетін түзудің проекциясы нүкте болып табылады.
Мысал. Нүктенің бір проекциясы бойынша кеңістікте нүктенің орнын көрсете алмау мүмкіндігі екінші қасиетінің нәтижесі болып табылады. Бұл үшін проекцияның түрлі ортасынан жүргізілген екі проекцияланатын түзулермен алынатын нүктенің екі проекциясы қажет (1.1. б сурет).
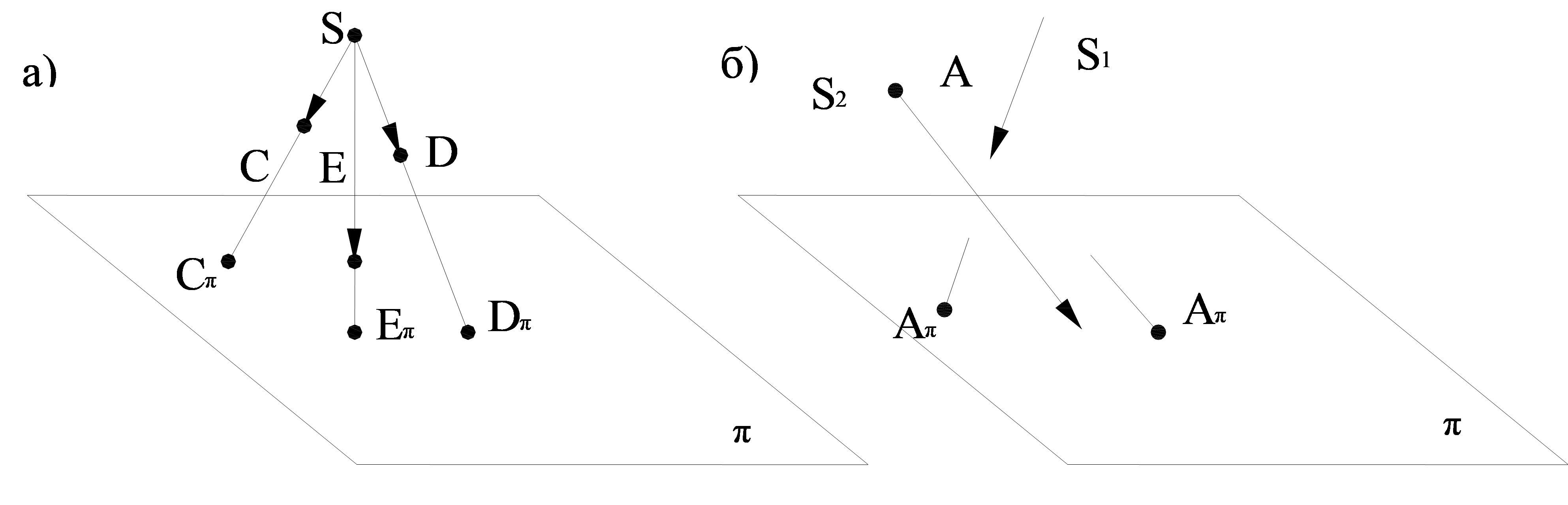
1.1 сурет – Орталық проекциялау тәсілімен нүктелерді жазықтыққа проекциялау
π – проеция жазықтығы; S – проекция ортасы; С, Е, D – проекцияланатын нүктелер; Сπ, Еπ, Dπ – С, Е, D нүктелерінің π жазықтығындағы орталық проекциялары.
Параллель проекциялау π жазықтығының жағдайымен және S проекциялау бағытымен толығымен анықталады. Проекцияланатын сәулелер өзара бір-біріне параллель болса, онда мұндай проекциялау параллель проекциялау деп аталады. Параллель проекциялау орталық проекциялар арқылы емес, олар S проекциялау бағытына параллель арқылы іске асады (1.2 сурет). Осы жағдайдағы нүктелердің проекцияларын параллель проекциялар деп атайды.

1.2 сурет – Нүктелерді параллель проекциялау тәсілімен проекциялау
π – проекция жазықтығы; S – проекция бағыты; С, D, Е – проекцияланатын нүктелер; Сπ, Dπ, Еπ – С, D, Е нүктелерінің π жазықтығындағы параллель проекциялары
Параллель проекциялау қисық бұрышты (проекцияланатын түзу мен проекция жазықтығының арасындағы бұрышы 900 тең емес, 1.3-сурет) және тікбұрышты (бұрыш 900 тең, 1.4-сурет) болып бөлінеді.

1.3 сурет – С және D нүктелердің параллель қисық бұрышты проекциялары
π – проекция жазықтығы; S2, S1 – проекция бағыттары; С, D – нүктелер; Сπ, Dπ – С, D нүктелерінің π жазықтығындағы қисық бұрышты проекциялары
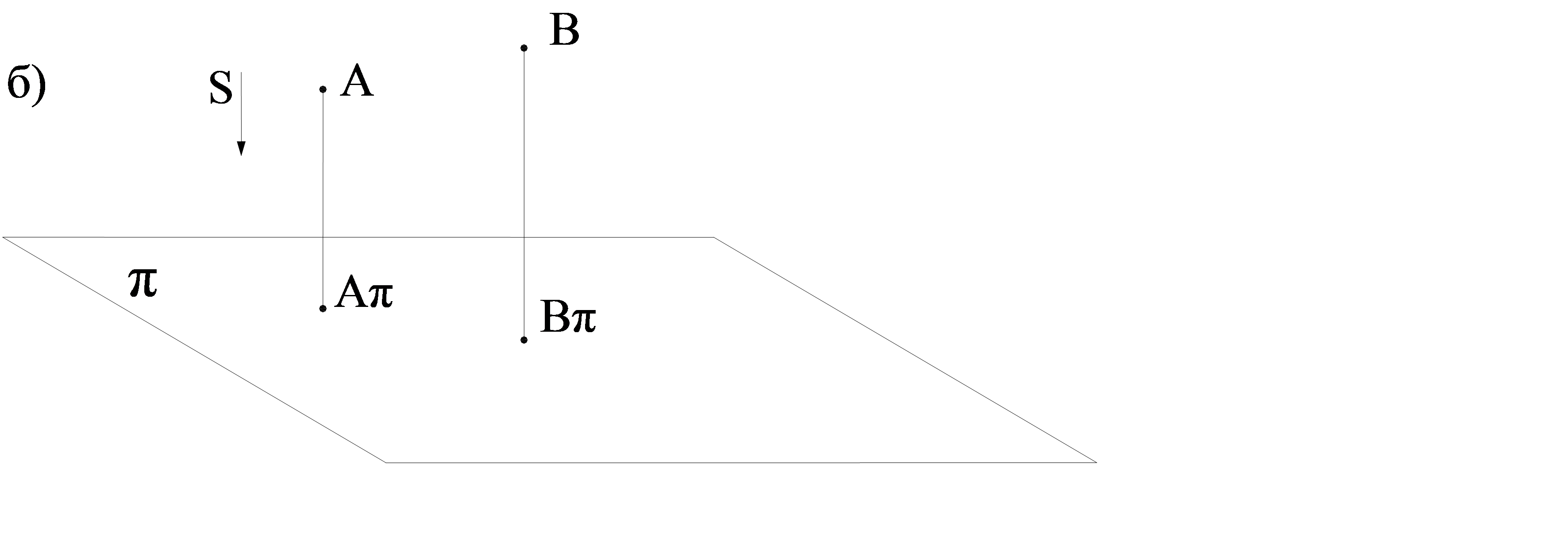
1.4 сурет – А және В нүктелерінің параллель тікбұрышты проекциялары
π – проекция жазықтығы; А, В – проекцияланатын нүктелер; S – проекция бағыты; А π, В π – А, В нүктелерінің π жазықтығындағы қисық бұрышты проекциялары
Әр қарастырған тәсілдердің өзінің кемшіліктері мен артықшылықтары бар. Бұл тәсілдер сызудың қандай мақсатпен орындалуына байланысты қолданылады. Дайындалатын заттың жасалуына арналған сызуды орындау үшін ортогональ проекциялау қолданылады. Қисық бұрышты, параллель проекциялау негізінен аксонометриялық бейнені алу үшін қолданылады, ал орталық – перспективалы бейнелерді құрастыруда қолданылады.
1.1.2 Блок. Бір және екі проекция жазықтықтарына ортогональ проекциялау
Ортогональ проекциялау параллель проекциялаудың дербес жағдайы, сондықтан нысанның проекциялау бағыты проекция жазықтығына перпендикуляр болады. Орталық проекциялау бойынша ортогональ проекциялаудың қосымша келесі қасиеттерін көрсетуге болады:
- проекция жазықтығына параллель түзу мен жазықтық оған нақты өлшеміне проекцияланады;
- проекция жазықтығына параллель емес түзу мен жазықтықтың проекциясы түзу мен жазықтықтың нақты өлшемдерінен әрқашанда кем;
- проекция жазықтығына перпендикуляр түзу мен жазықтықтың проекциялары сәйкесінше нүкте мен түзу түрінде бейнеленеді.

1.5 сурет – Нүктені бір проекция жазықтығына ортогональ проекциялау
π - проекция жазықтығы; А, В - проекцияланатын нүктелер; S - проекция бағыты; Аπ , Вπ - А, В нүктелерінің π жазықтығындағы перпендикуляр проекциялары
Нүктенің бір проекциясы кеңістікте нүктенің орналасуын анықтай алмауына байланысты, екі проекция жазықтығына проекциялау қолданылады. Екі проекция жазықтығына проекциялау кезінде проекциялау құралы ретінде А1Ах және Ах А2 қосымша байланыс сызықтары енгізіледі. Бір нүктенің проекцияларын жалғастыратын түзулерді проекциялық байланыс сызықтары деп атайды. Проекция жазықтықтары бір-біріне 900 бұрышпен орналасады. π1 проекция жазықтығын горизонталь проекция жазықтығы, ал π2 проекция жазықтығын фронталь проекция жазықтығы деп атаймыз.
π1 және π 2 екі проекция жазықтығы жүйесінде проекция өстері келесідей бөлінеді: ОХ – абсциссалар өсі, ОУ – ординаталар өсі, ОZ – аппликаталар өсі. ОХ өсі солға, ОУ өсі бақылаушыға, ОZ өсі жоғарғыға оң (таңбалы) бағытқа қабылданған. Кері бағыттары теріс (таңбалы) қабылданған.
Нүктенің горизонталь проекция жазықтығындағы проекциясы горизонталь проекциясы, ал фронталь проекция жазықтығындағы - фронталь проекция деп аталады. Нүктенің екі проекциясы нүктенің кеңістіктегі орнын анықтайды.
Мысал 1.1. 1.6 суретте берілген кеңістікті макетін жазықтыққа өзгертеміз. Бұл үшін нүктенің өзін жоямыз, тек қана оның проекциясы мен байланыс сызығын қалдырамыз. π проекция жазықтығын 1.7а суретінде көрсетілгендей π2 жазықтығымен түйіндесуіне дейін ОХ өсінің айналасында айналдырамыз. Әрі қарай проекция жазықтығын алып тастаймыз, тек қана оны жобалаймыз. Өзгеріс нәтижесінде жазықты сызба пайда болады (1.7в сурет), оны нүктенің кешенді сызбасы немесе Монж эпюрі деп атайды. Эпюрде нүктенің координаттары көрсетілген, олар бойынша нүктенің кеңістікте орнын анықтауға болады.
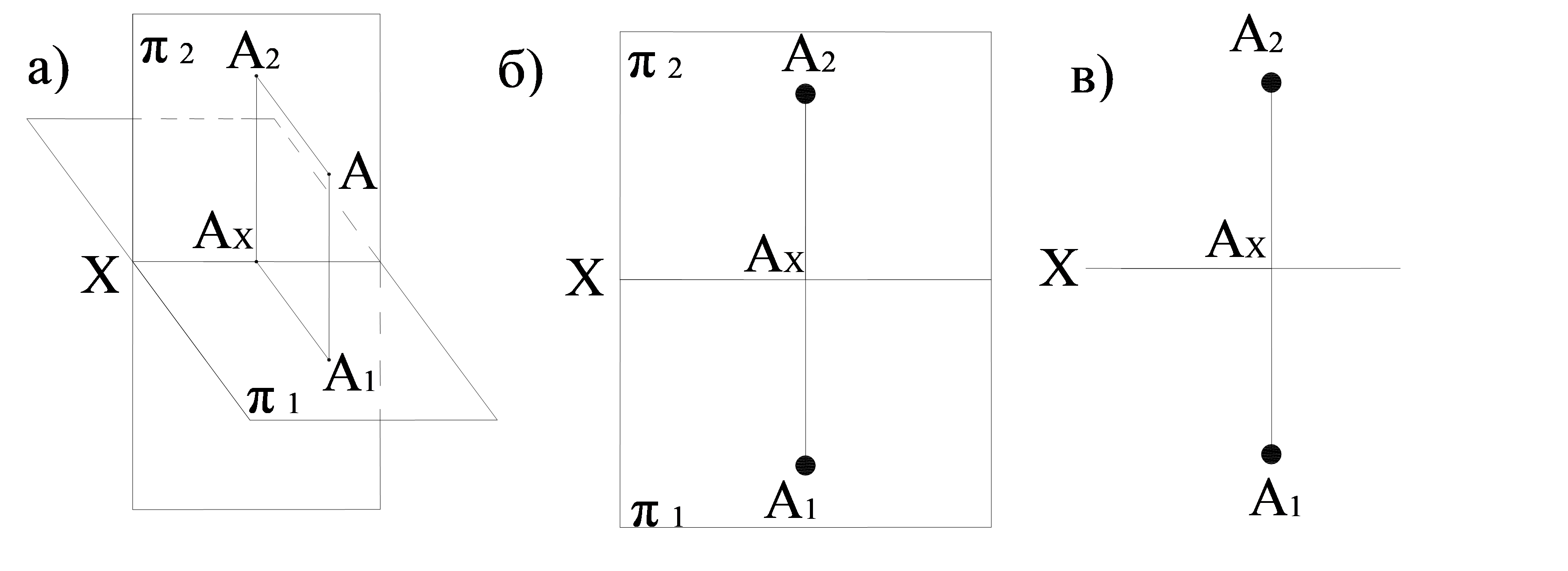
1.6 сурет – Екі проекция жазықтығында нүктені проекциялау
А – А нүктесінің кеңістіктегі орналасуы; А1 – А нүктесінің горизонталь проекциясы; А2 – А нүктесінің фронталь проекциясы; Ах – х өсімен байланыс сызығының қиылысқан нүктесі; π1 – горизонталь проекция жазықтығы; π2 - фронталь проекция жазықтығы
1.1.3 Блок. Үш проекция жазықтығында ортогональ проекциялау
Егер геометриялық нысанның құрылымы күрделі болса, үш проекция жазықтығына проекциялау қажет болады. Екі проекция жазықтығы жүйесіне үшінші π 3 профиль проекция жазықтығын енгіземіз 1.7 сурет). Геометриялық фигура үш проекция жазықтық жүйесіндегі π1, π2, π3 жазықтықтарына проекцияланады және бір нүктенің үш проекциясы табылады: горизонталь, фронталь және профиль проекциялары.

1.7 сурет – А нүктесін үш проекция жазықтығына ортогональ проекциялау
π1 – горизонталь проекция жазықтығы; π2 – фронталь проекция жазықтығы; π3 – профиль проекция жазықтығы; А – А нүктенің кеңістіктегі орны; А1 – А нүктенің горизонталь проекциясы; А2 – А нүктенің фронталь проекциясы; А3 – А нүктенің профиль проекциясы; Ах – х өсімен байланыс сызығының қиылысқан нүктесі; Ау – у өсімен байланыс сызығының қиылысқан нүктесі; Аz – z өсімен байланыс сызығының қиылысқан нүктесі
Егер барлық үш проекция жазықтықтарын геометриялық кеңістікте жан-жағынан жалғастыра берсе, онда ол үш жазықтық сегіз бөлікке бөлінеді, оны октант деп атайды (1.8 сурет).
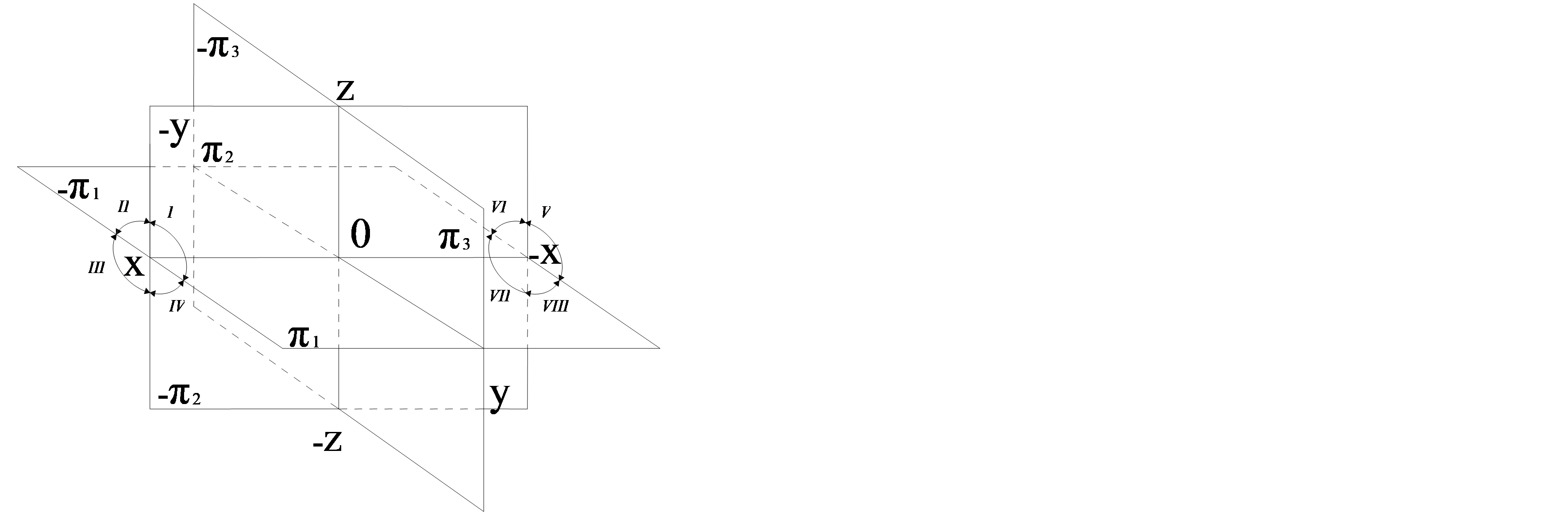
1.8 сурет – Октанттардың проекция жазықтықтарында орналасуы
Октанттар ОХ, ОУ және ОZ координат өстері бойынша әр түрлі таңбалармен сипатталады. Әр түрлі октанттағы нүкте координаттарының таңбалары 1- кестеде берілген.
Кесте 1
|
Координат өсі бойынша белгілер |
Октант нөмері |
|||||||
|
I |
II |
III |
IV |
V |
VI |
VII |
VIII |
|
|
ОХ |
+ |
+ |
+ |
+ |
- |
- |
- |
- |
|
ОУ |
+ |
- |
- |
+ |
+ |
- |
- |
+ |
|
ОZ |
+ |
+ |
- |
- |
+ |
+ |
- |
- |
Мысал.
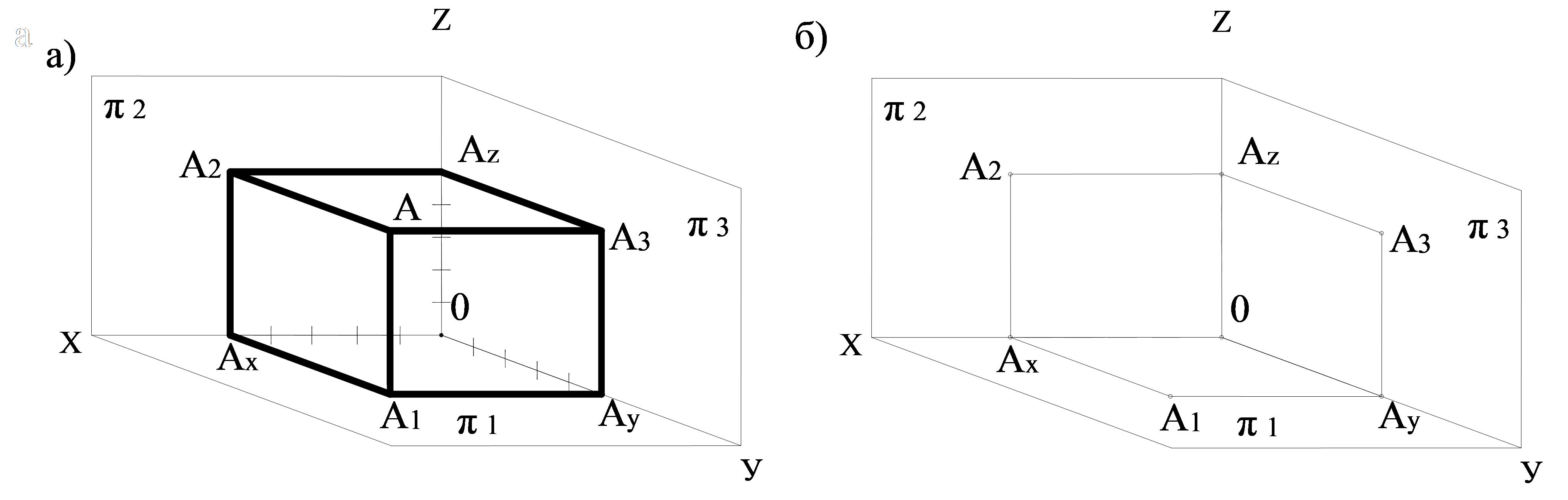
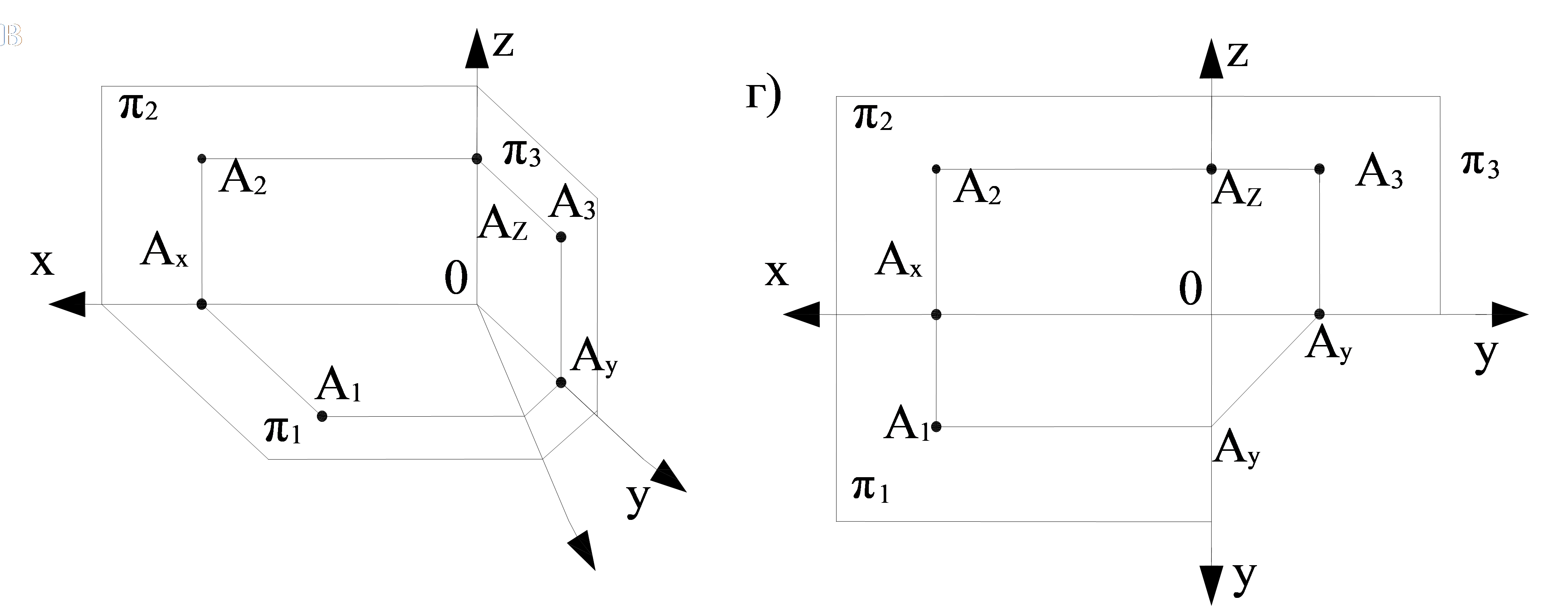
1.9 сурет, 1 бет – Эпюрде нүктенің проекциясымен бірге бірінші октантанттың кеңістікті моделінің трансформациясын тұрғызу
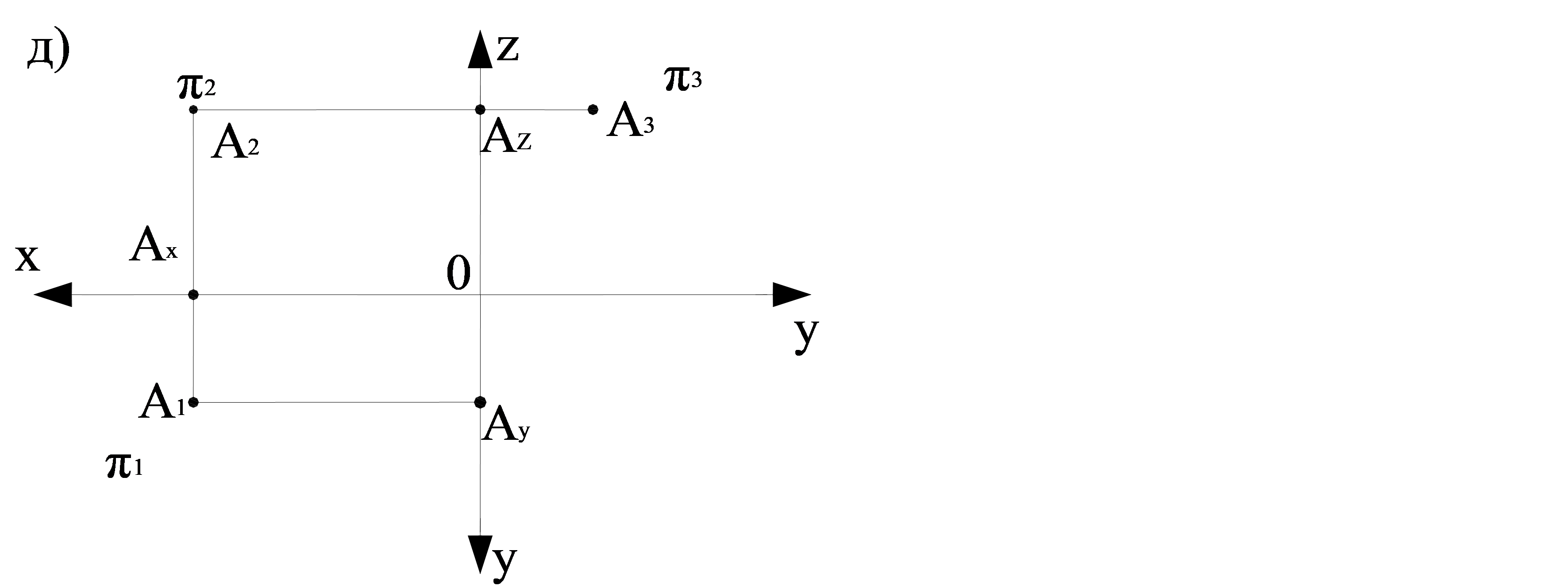
1.9 сурет, 2 бет
π1 – горизонталь проекция жазықтығы; π2 – фронталь проекция жазықтығы; π3 – профиль проекция жазықтығы; А – А нүктесінің кеңістіктегі орны; А1 – А нүктесінің горизонталь проекциясы; А2 – А нүктесінің фронталь проекциясы; А3 – А нүктесінің профиль проекциясы; Ах, Ау, Аz – х, у, z өстерімен байланыс сызығының қиылысқан нүктесі
Эпюрде нүктенің проекциясымен бірге бірінші октантанттың кеңістікті моделінің трансформациясын тұрғызу керек (1.9 сурет):
- геометриялық нысанын алып тастайды, бірақ оның проекциясын байланыс сызықтарымен сақтайды (1.9 б сурет);
- ойша ОУ өсі бойынша октантты ″кеседі″ және π1 мен π2 жазықтықтарын 1.9 в суретінде көрсетілгендей етіп бұрады;
- үш проекция жазықтығының өсімен, сызық байланысымен және нүктенің проекциясымен жазықтықты жүйесі алынады (1.9 г суретіне қараңдар).
- проекция жазықтықтарын алып тастайды және тек өстерді ғана қалдырады. Түрлендіру нәтижесінде үш проекция жазықтығында нүктенің кешенді сызбасын немесе Монж эпюрасын алады (1.9 д сурет). Эпюрде ОУ екі өсі пайда болғанын аңғаруға болады: бір өсі π1 жазықтығына қатысты, ал екіншісі, жұлдызшамен * белгіленгені, π2 жазықтығына қатысты.
Үш проекциядағы нүктенің эпюрасы инженерлік сызба және техникалық сызу негізіне енген.
Кеңістіктегі сызбаның үш проекция жазықтығына ортогональ проекциялаудан шығатын Монж эпюрасының қасиетін қарастырамыз:
- А нүктесінің горизонталь прекциясы Х және У координаталарымен анықталады, әрі оны салу үшін У координатасы ОУ вертикаль өсі бойымен шегеріледі;
- А нүктесінің фронталь проекциясы Х және Z координаталарымен анықталады;
- А нүктесінің профиль проекциясы Z және У координаталарымен анықталады, әрі У координатасы ОУ* вертикаль өсі бойымен шегеріледі;
- нүктенің горизонталь және фронталь проекциялары ОХ өсіне перпендикуляр болатын бір байланыс сызығының бойында жатады;
- нүктенің фронталь және профиль проекциялары ОZ өсіне перпендикуляр болатын бір байланыс сызығының бойында жатады;
- АхА1=АzА3 байланыс сызығындағы кесінділер өзара тең, себебі у координаттары бірдей.
Мұндай нәтиже кеңістікті макетін қарастырғанда шығады:
- жоғарыдағы қасиеті бойынша Монж эпюрасының негізгі қасиеті шығады – нүктенің екі проекциясы бойынша үшіншісін салуға болады.
Жоғарыдағы қарастырылғандар октантта жалпы жағдайда орналасқан нүктеге қатысты. Бірақ нүкте проекция жазықтықтарына немесе өстерге жатуы мүмкін. Мұндай жағдайдағы нүктелерді дербес жағдайдағы нүктелер деп атайды.
Мысал. π1, π2, π3 жазықтығында А (5; 4; 6) нүктесінің проекциясын салу қажет (1.10 сурет). Бұл координаталар оң таңбалы, және де бірінші октантада жатады. Нүктенің бейнесін салу және кеңістікті модельде оның проекциясын салу координатты тік бұрышты параллелограмманың көмегімен жүзеге асырылады. Сондықтан координат өстерінде кесінділер шегеріледі, яғни кесінді ұзындықтарына сәйкес: ОАх = 5, OАy = 4, OАz = 6. Осы кесінділерде (ОАx, Оаy, ОАz) тік бұрышты параллелпипед саламыз. Оның төбелерінің бірі берілген А нүктесін анықтайды. Нүктенің екі проекциясы бір байланыс сызығында жатады; нүктенің екі проекциясы оның үшінші проекциясын анықтайды; байланыс сызықтары сәйкес проекция өстеріне перпендикуляр.
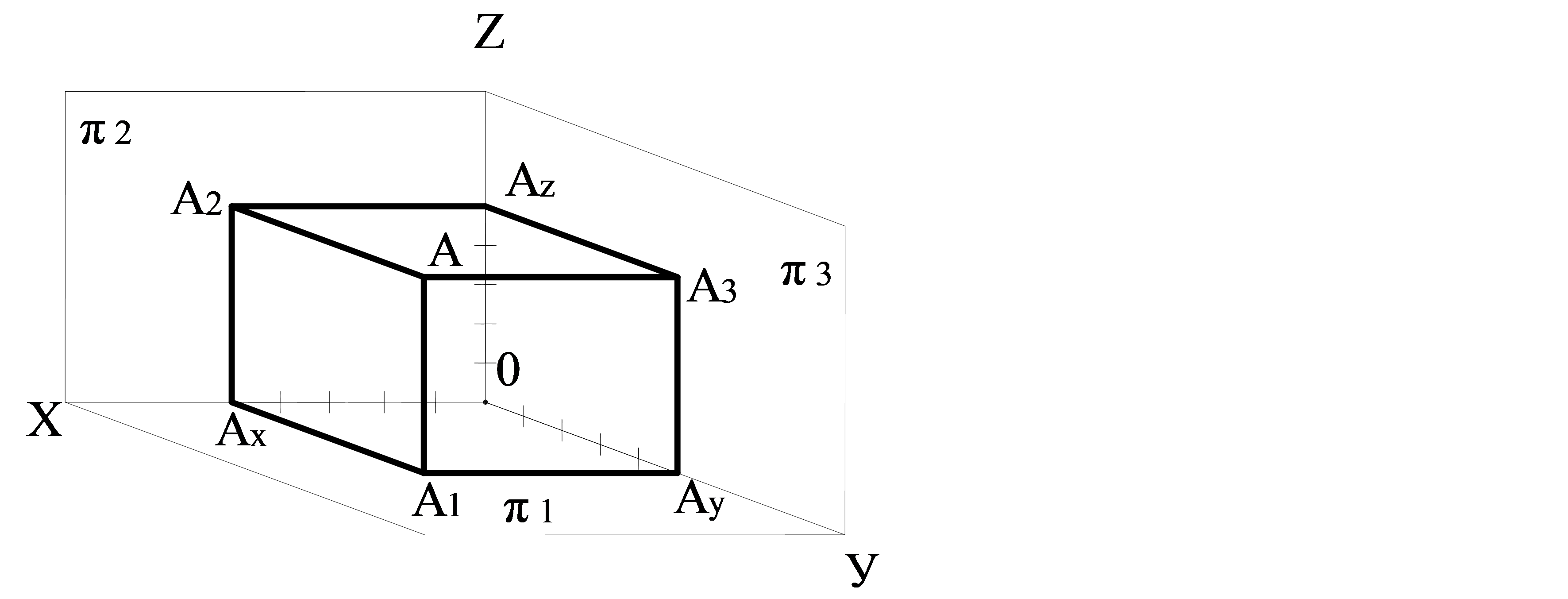
1.10 сурет – А нүктесінің үш проекциясын салу
Мысал. А нүктесінің А1, А2 проекциялары берілген, онда олар кеңістікте нүктенің орнын анықтай ала ма? (1.11 сурет)
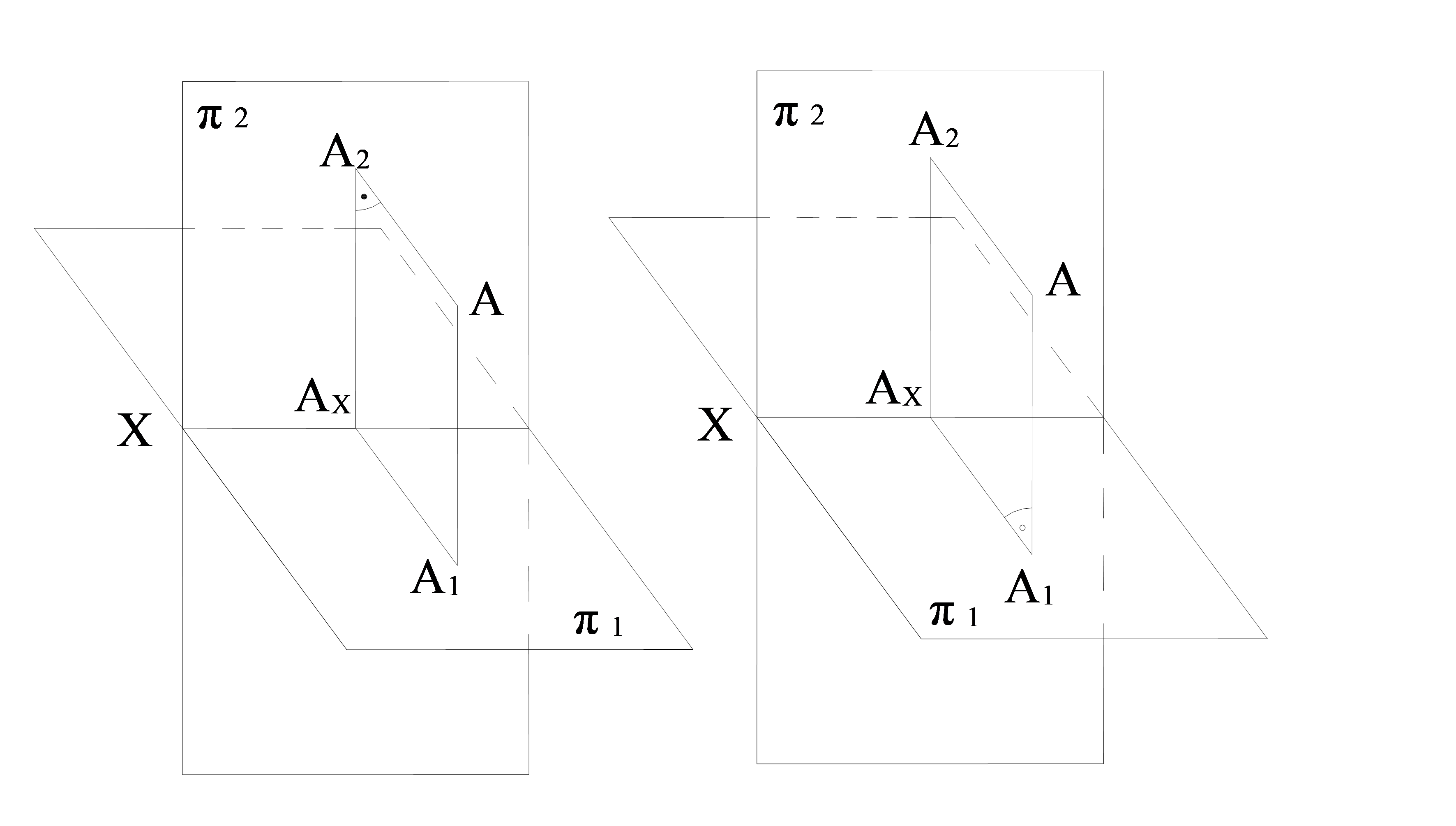
1.11 сурет – Нүктенің кеністіктегі орнын табу
А1 нүктесінен π1 жазықтығына перпендикуляр тұрғызамыз. А2 нүктесінен π2 жазықтығына перпендикуляр тұрғызамыз (1.11 сурет). А А1 АхА2 фигурасы тік бұрышты болады. А нүктесі бір жазықтықта қиылысатын екі перпендикулярда жататын нүкте және ол жалғыз.
Координаттары бойынша нүктенің проекциясын тұрғызу
Егер қандай да бір нүктенің координатасы А(х, у, z) берілген болса, онда нүктенің проекциясын келесі тәсілмен тұрғызады: ОХ өсі бойынша абсциссаны саламыз; сонан соң тік сызығын тұрғызамыз; ары қарай онда ОУ өсі бойынша ординатаны және ОZ өсі бойынша аппликатаны саламыз (ОХ өсінен у, z координаталарының таңбаларына байланысты жоғары немесе төмен). ОУ өсі бойынша А нүктесінің А1 горизонталь проекциясын табамыз, ал ОZ өсі бойынша нүктенің фронталь проекциясын табамыз. Нүктенің А3 профиль проекциясын А1 және А2 ( А нүктенің горизонталь және фронталь проекциялары) арқылы табамыз.
Мысал. С(5;7;6) және D(10;5;4) нүктелерінің проекцияларының эпюрасын тұрғызу керек (1.12 сурет). Горизонталь проекциясының орны х және у координаталары арқылы, ал фронталь проекциясы – х және z координаталарымен, профиль проекциясы – у және z координаталарымен анықталады. Онда у ординатасы горизонталь проекцияның орнын, ал аппликата – фронталь проекцияның орнын сипаттайды.
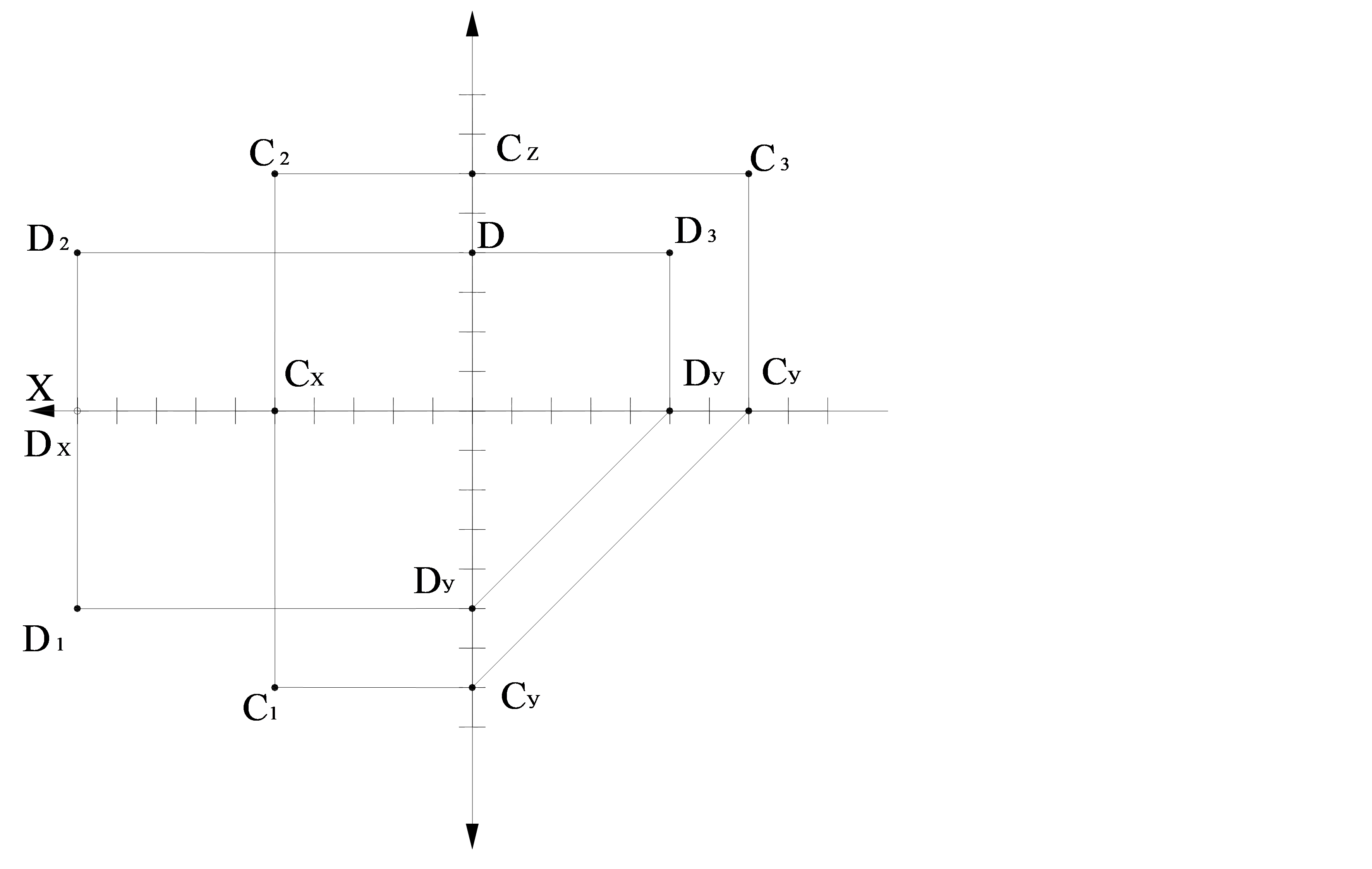
1.12 сурет – С және D нүктелердің проекцияларын тұрғызу
Ұсынылған теориялар төмендегі жағдайларға негізделеді:
1) өзара перпендикуляр π1 және π2 жазықтықтар арқылы барлық кеңістіктер 4 бөлікке бөлінеді, немесе үшінші өзара перпендикуляр π3 жазықтығын еңгізу арқылы 8 октанттарға бөлінеді;
2) бұл жазықтыққа кеңістікті бейнесі тікбұрышты (ортогональ) проекциялаудың көмегімен іске асады;
3) кеңістікті бейнені жазықты бейнеге айналдыру үшін π2 жазықтығы қозғалыссыз, ал π1 жазықтығы х өсі бойында айналады, яғни π1 жартылай жазықтығы π2 теріс жартылай жазықтығымен қосылады және π1 теріс бөлігі – π2 оң бөлігімен қосылады;
4) π3 жазықтығы π2 жазықтығымен қосылғанға дейін z өсінің бойында айналады;
5) бейнелерді тік бұрышты проекциялауда π1, π2 және π3 жазықтықтарында тұрғызылған кескіндер проекциялар деп аталады;
6) π1, π2 және π3 жазықтықтары онда бейнеленген проекцияларымен бірге жазықтықты кешенді сызбаны немесе эпюрасын құрайды;
7) x, y, z өстерімен π бейнесінің проекцияларын байланыстыратын сызықтар проекциялық байланыс сызықтары деп аталады;
8) кеңістіктегі бейнелерді нақты анықтау үшін үш өзара перпендикуляр π1, π2, π 3 жазықтықтар жүйесі қолданылуы ықтимал;
9) есептің шартына байланысты бейнелеуге π1, π 2 немесе π1, π2, π 3 жүйесін таңдауға болады;
10) π1, π2, π3 жазықтықтар жүйесін декартты координат жүйесімен қосуға болады, бұл нысанды тек қана графикалық немесе (вербальды) бейнелік түрін ғана емес, сонымен қатар аналитикалық (сандар көмегімен) түрде беруге мүмкіндік жасайды. Сұлбаны бейнелеудің осындай тәсілі келесі позициялық есептерді шешуге мүмкіндік береді:
- проекция жазықтықтарына қатысты нүктенің орналасуы (жалпы жағдайы, жазықтықтың, өстердің жататындары);
- нүктелердің ширекте орналасуы (нүктенің қандай ширекте орналасуы);
- нүктелердің бір-біріне қатысты орналасуы (проекция жазықтығына және көрерменге қатысты жоғары, төмен, жақын және алыс орналасуы);
- проекция жазықтығына қатысты нүктенің проекциясының орналасуы (тең қашықтықта, жақын, алыс).
Тапсырмалар:
С, D және Е нүктелерінің координаталарын және олардың кеңістіктегі орнын анықтау (сурет 1.13 а.б.).

1.13 сурет
Тапсырмалар:
Берілген АВС үшбұрышының екі төбесінің проекциялары белгілі деп қарастырайық, оның орталық проекциясын салуды аяқтау керек (1.14 сурет).

1.14 сурет
Өзіндік талдау үшін сұрақтар:
1) Жазықтықта нәрсе кескіні қалай салынады?
2) Проекция деген не?
3) Орталық проекциялау деген не?
4) Параллель проекциялау деген не?
5) Тік бұрышты проекция деп нені айтады және оның ерекшілігі неде?
6) Кескін жазықтықта қалай салынады?
7) Жазықтыққа перпендикуляр деп нені айтады?
8) z өсі қандай жазықтықтардың қиылысу сызығы болып табылады?
9) у өсі қандай жазықтықтардың қиылысу сызығы болады?
10) Проекциялық байланыс сызықтары деген не?
11) Абсцисса, ордината және аппликатор деген не?
12) Эпюра деген ен?
13) Нүктенің горизонталь, фронталь және профиль проекциялары қандай координаттар арқылы анықталады?
14) F (20; -20; -30) нүктесі қандай ширекте орналасады? F нүктесі қай проекция жазықтығынан алшақ қашықтаған?
15) Октант деген не ?
16) Октанттын белгіліре неден байланысты?
17) Нүктенің π1 жазықтығынан ара қашықтығы қандай проекциядан қандай өске дейінгі қашықтығымен анықталады?
18) Нүктенің фронталь және профиль проекциясында проекциялық байланыс сызықтары қалай орналасады? Көрсетіңіз.
19) Ортогональ проекция әдісі (Монж әдісі) нені білдіреді?
20) Нүктенің горизонталь, фронталь және профиль проекциялары деп нені айтады?
21) Нүктенің кешенді сызбасы (эпюр) деген не және оны тұрғызу механизмі?
22) Нүктенің координаталары деген не?
23) Сызба бойынша нүктеден проекция жазықтығына дейінгі қашықтықты қалай анықтауға болады?
24) Сызбада нүктенің горизонталь және фронталь проекциялары тоғыса ала ма?
25) Бір проекция жазықтығында жатқан нүктенің проекциялары қайда орналасқан?
26) Нүктенің координаттарының біреуі нөлге тең болуы нені білдіреді?
Бақылау жұмысы
Есеп №1. Нүктелердің берілген координаттары бойынша эпюрада олардың проекцияларын салыңдар және олардың проекция жазықтықтарына қатысты орналасуын анықтаңдар (2 кесте).
кесте 2
|
|
А |
В |
С |
D |
Е |
|
х |
95 |
55 |
95 |
95 |
30 |
|
у |
65 |
25 |
25 |
65 |
65 |
|
z |
20 |
90 |
90 |
90 |
90 |
Есеп № 2
Кешендік сызбада нүктелердің проекцияларын тұрғызу керек: А(0; -15; 45); В(25; 35; - 40); С (- 6; 30; 25); Е (25; - 45; 55); D(- 23; 65; 25)
Әдебиеттер
Негізгі:
1 Есмуханов Ж. М. Сызба геометриясы есептері. – Алматы: Білім,1995. – 272 б.
2 Ақпанбек Ғ. Сызба геометрия. – Алматы,1998. – 208б.
3 Ақпанбеков Ғ. Сызба геометрия. – Алматы: «Қазақ универсиверситеті», 1992. – 120 б.
4 Миронова Р.С., Миронов Б.Г. Сборник заданий по черчению. – М.: Высшая школа, 2004. – 355 с.
Қосымша:
5 Чекмарев А.А. Инженерная графика. – М.: Высшая школа, 1988. – 365с.
6 Короев Ю.И.Черчение для строителей. – М.: Стройиздат, 2001. – 256 с.