Модуль Сызбаны түрлендіру тәсілдері
Сызбаны түрлендіру тәсілдері геометриялық нысандардың нақты өлшемдерін немесе геометриялық нысандардың арасындағы қысқа ара қашықтықты анықтайтын метрлік есептерді шешу үшін қолданылады.
Бұл тәсілдердің басты мақсаты – қарастырылып отырған геометриялық нысан қандай да бір проекция жазықтығына параллель орналасқандай етіп кешенді сызбаны түрлендіру қажет.
Кешенді сызбаны осындай түрлендіру екі негізгі тәсілмен жүзеге асырылады:
- айналдыру тәсілі. Мұнда проекция жазықтығы жүйесін өзгеріссіз қалдырады, ал берілген геометриялық нысанның қалпын біз қарастырып отырған жазықтық немесе түзу проекция жазықтығының біріне параллель болатындай етіп бір немесе таңдалған екі өстің айналасында айналдыру жолымен өзгертеді. Әдетте айналу өсі ретінде проекция жазықтығының біріне перпендикуляр болатын түзуді таңдайды.
- проекция жазықтықтарын алмастыру тәсілі. Бұл тәсілде кеңістіктегі геометриялық нысаннның орналасуын өзгеріссіз қалдырып, ал бізге қажет түзулер немесе жазықтықтар проекцияның жаңа жазықтықтарының біреуіне параллель болатын етіп, бір немесе тізбектей екі проекция жазықтығын алмастырады.
Осы тәсілдермен геометриялық нысандарды проекцияланатын қалпына келтіру есептерін де шығаруға болады.
4.1 Блок. Проекцияланатын өстің айналасында айналу тәсілі
4.1.1 Блок. Нүктенің айналу
Мысал. π1 проекциясының горизонталь жазықтығына перпендикуляр і өсінің айналасында В нүктесінің айналуын қарастырайық (4.1 сурет). Айналу өсі π 1 жазықтығына нүкте болып проекцияланады, ал π2 жазықтығына ОХ өсіне перпендикуляр болатын түзу болып проекцияланады. В нүктесінің қозғалу траекториясы π1 жазықтығына параллель болатын айналу жазықтығында жататын шеңбер болады. Оның айналу центрі өс бойында жатқан О нүктесі және айналу радиусы ОВ болады. Нүктенің қозғалу траекториясы π1 жазықтығына нақты өлшемге проекцияланады, ал π 2 жазықтығына – ОХ өсіне параллель болатын түзу ретінде проекцияланады. Щеңбердің радиусы да π1 жазықтығына нақты өлшемге проекцияланады. Сонымен, В нүктесінің В1 горизонталь проекциясы шеңбер бойымен қозғалады, ал В2 фронталь проекциясы – ОХ өсіне параллель болатын түзумен қозғалады.
В нүктесін α бұрышына бұру үшін, бұл бұрышты горизонталь проекцияда қалдырады және осыдан жаңа В1' жағдайында В нүктесінің В1 горизонталь проекциясын алады. Осы нүктенің В2' фронталь проекциясын проекциялық байланыс сызықтары арқылы табады. Бұл проекциялық байланыс сызықтары В1' нүктесінен ОХ өсіне параллель В2 нүктесінен жүргізілген түзумен қиылысуына дейін жүргізіледі.
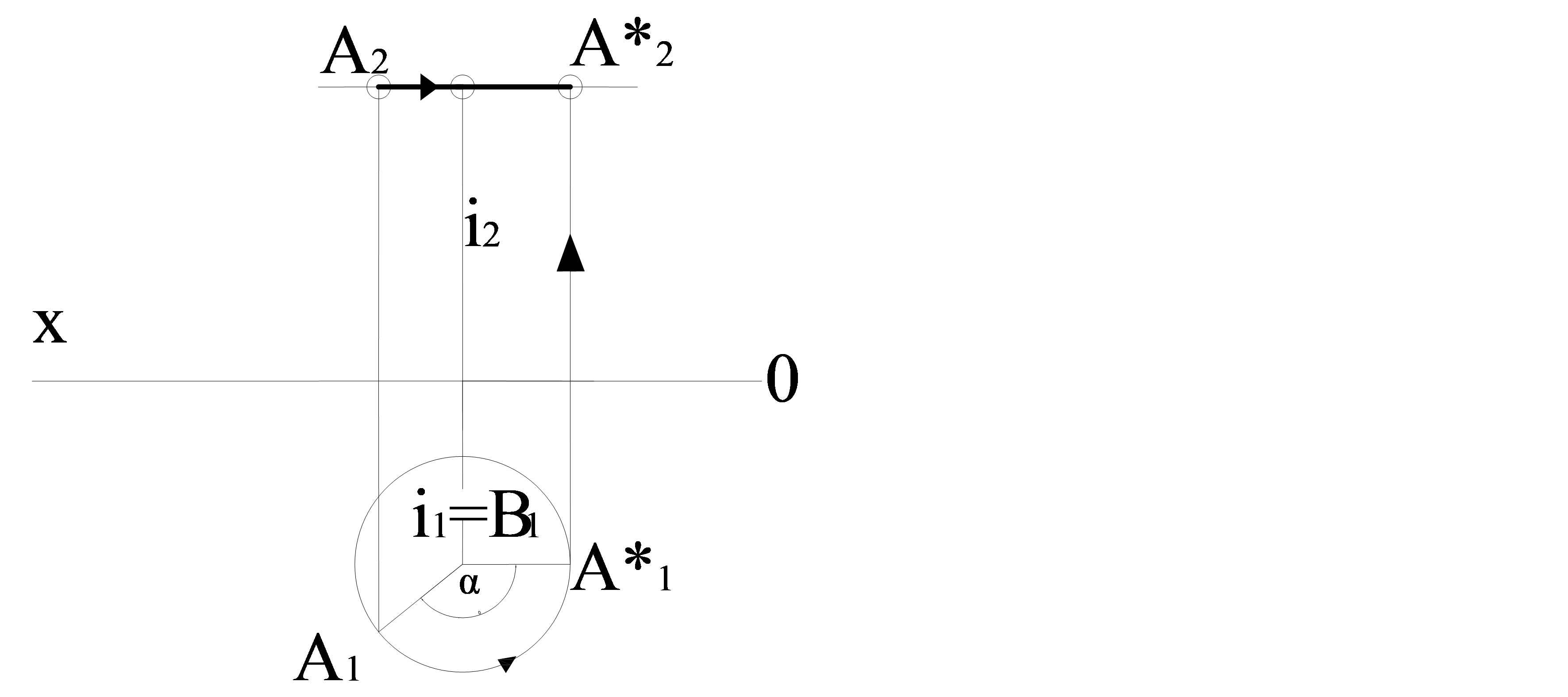
4.1 сурет – Горизонталь- проекциялаушы өсінің айналасында В нүктесінің айналуы
4.1.2 Блок. Түзу сызықты айналдыру
Түзу сызық екі нүктемен анықталғандықтан, түзудің айналуы түзудегі орналасқан нүктелердің айналуына әкеп соғады.
Егер де айналу өсі түзу кесіндісінің шеткі нүктелерінің бірі арқылы өтсе салу жеңілдеу орындалады. Айналу барысында бұл нүкте қозғалыссыз қалады, сондықтан оның жаңа орналасуын табу үшін осы түзудің кез келген басқа нүктесін бұру жеткілікті. Жалпы жағдайдағы түзудің СD кесіндісінің ұзындығын анықтау үшін, мысалы π1 жазықтығына перпендикуляр D нүктесі арқылы і айналу өсін жүргіземіз және СD кесіндісі π2 жазықтығына параллель болатындай етіп, СD кесіндісін айналдырамыз. D нүктесін қозғалыссыз қалады (4.2 сурет), C1 нүктесін белгісіз α бұрышына бұрамыз, сонда СD бұрылған кесіндісінің C1'D1' горизонталь проекциясы ОХ өсіне параллель болады. Оның C2' D2 фронталь проекциясының ұзындығы СD кесіндісінің ұзындығына тең болады, сондай-ақ C'D фронталь қалпында орналасады.
Сонда α бұрышы – π1-ге СD көлбеу бұрышы, сондықтан қандай да бір жазықтық проекциясына перпендикуляр өстің айналасында түзуді айналдырғанда бұл жазықтыққа көлбеу бұрышы өзгермейді. Түзудің кесіндісінің ұзындығын π 2-ге перпендикуляр орналасқан өстің айналасын айналу арқылы табуға болады. Осыдан СD түзуінің π2 жазықтығына β көлбеу бұрышы анықталады.
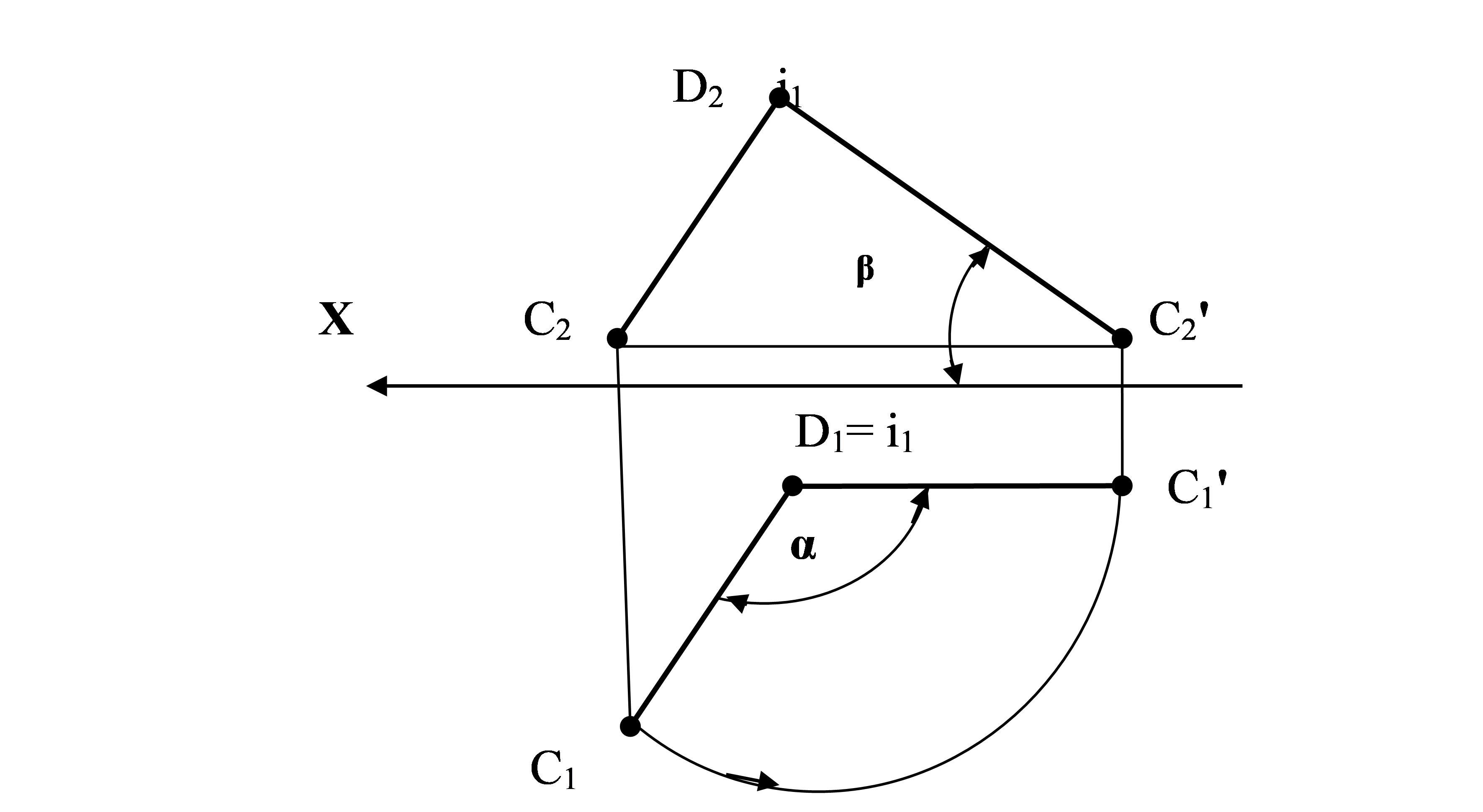
4.2 сурет – Түзуді горизонталь-проекцияланатын өсті айнала айналдыру
4.2 Блок. Жазық-параллель орын ауыстыру тәсілі
Жазық-параллель орын ауыстыру тәсілі проекцияланатын осьті айналу тәсілінің дербес жағдайы болып табылады, яғни геометриялық нысанды тек қана айналдырып қана қоймай, сонымен қатар проекция жазықтарының біріне параллель болатын жазықтықта орнын ауыстыруға болады. Бұл тәсіл келесі есептерді шешу барысында қолданылады:
- түзу сызықты түзу деңгейдің бойында немесе проекцияланатын түзудің бой ында орнын ауыстыру;
- жалпы жағдайдағы жазықтықты проекцияланатын немесе деңгей жазықтығына түрлендіру.
4.2.1 Блок. Түзу сызықты түрлендіру
Түзу сызықтың кесіндісін шеткі нүктелері проекциялардың қандай да бір жазықтығына параллель болатындай етіп жаңа орынға ауыстырғанда, осы жазықтыққа кесінді прокциясының ұзындығы өзгеріссіз қалады (4.3сурет).
Алдымен жалпы жағдайдағы түзу сызықтың кесіндісін горизонталь қалпына, ал кейін фронталь-проекциялаушы қалпына түрлендіреміз. Ол үшін СD кесіндісінің C2D2 фронталь проекциясын сызбаның кез келген жерінде ОХ өсіне параллель (C2'D2'//ОХ) орналастырамыз. Сондықтан C1 мен D1 нүктелері жаңа орынға ОХ өсіне параллель түзу бойымен орын ауыстырады және сәйкесінше C2', D2'-мен байланыс сызықтарында жатады. Онда жаңа горизонталь проекциясы C1'D1' қалпында орналасыады. C'D' горизонталь болғандықтан, C1'D1' – CD кесіндісінің нақты өлшемі екені белгілі. Сосын C1'D1' ОХ өсіне перпендикуляр болғандай C1'D1'-ді жаңа орынға ауыстырамыз. Сонда C2''=D2'' болады, яғни CD проекцияланатын түзу қалпында орналасады. C1'D1' ұзындығы сәйкес келетін CD кесіндісінің нақты өлшемін анықтаған кезде, C2'D2' проекциясының ОХ өсінен алшақтығы ешқандай өзгеріс бермейді. Мұнда тек екі талаптың орындалуы маңызды: C2'D2'-ның C2D2 –ге тең және ОХ өсіне параллель болуы тиіс.
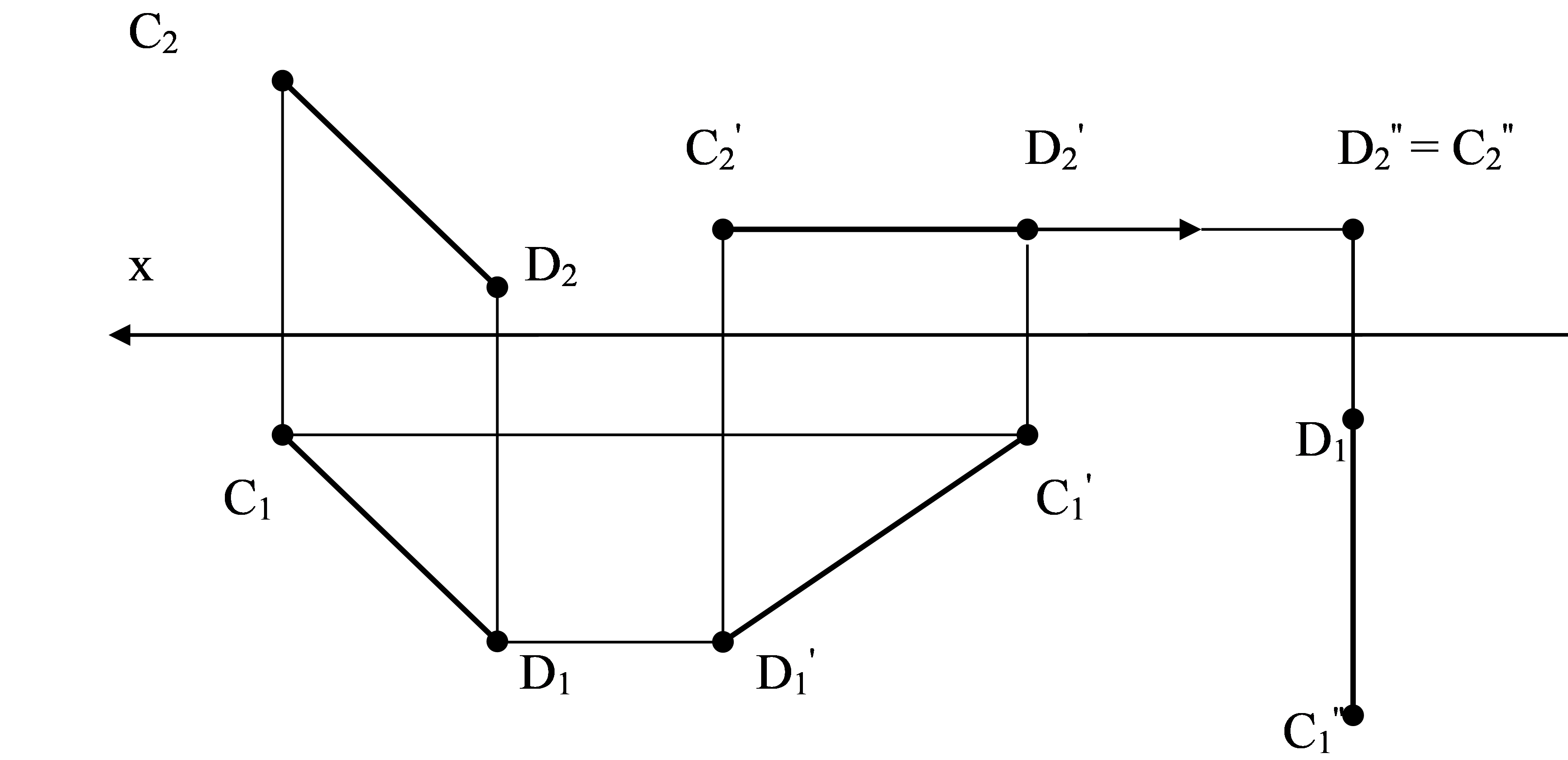
4.3сурет – Түзу сызықтың жазық-параллель орын ауыстыру
4.2.2 Блок. Жазықтықты түрлендіру >
Бұл тәсілдің көлемінде сызбаны тек бір түрлендірумен берілген есепті шешу мүмкін емес.
Мысалы. Жалпы жағдайдағы ΔCDF жазықтығын деңгейдің горизонталь жазықтығына түрлендіреміз.
Бұның шешімін ΔCDF-ны екі орын ауыстыруы арқылы жүзеге асыруға болады: алдымен – проекцияланатын қалпына келтіру арқылы, ал кейін – деңгейдің жазықтығының қалпына келтіру арқылы (4.4 сурет).
ΔCDF жазықтығын фронталь-проекциялаушы қалпына орналастырамыз. Содан кейін, алдымен ΔCDF жазықтығында горизонталь тұрғызып, ал кейін оны горизонтальдің h1 жаңа горизонталь проекциясы ОХ өсіне перпендикуляр болатындай етіп орнын ауыстыру қажет. Сонымен, ΔC1D1F1 горизонталь проекциясы жаңа қалпына өзінің нақты өлшемін өзгертпей көшеді. Сондықтан, бірінші кезеңдегі салу келесі ретте жүзеге асырылады: алдымен ΔC1D1С1 –ді жаңа қалпына орналастырамыз. Сол үшін одан бірнеше қашықтықта ОХ-ке перпендикуляр жүргіземіз, одан C1'K1' =C1K1 ұзындығын алып, сонымен C1 нүктесін ОХ өсінен еркін қашықтықта тұрғызамыз. Сосын, C1D1F1-дің өлшемдерін өзгертпей, h1 және h1' біріктіріп, жаңа орынға ауыстыру қажет. Ол үшін C1'нүктесінен C1F1 радиусының доғасын өткізіп, ал K1' нүктесінен K1F1 радиусын өткізу қажет. Доғалардың қиылысуында F1нүктесін аламыз. Ұқсас жағдайда K1-ді K1' қалпына ауыстырамыз.
Сонымен ΔC1D1F1-ді C1'D1'F1' жаңа жағдайында аламыз. Бұл жағдайда C,D, F нүктелерінің фронталь проекциялары ОХ өсіне параллель түзулер бойымен орын ауыстырады және сәйкесінше C1',D1',F1' нүктелерімен байланыс сызықтарында орын алады. ΔCDF фронталь-проекциялаушы қалпында орын алатындықтан, оның C2'D2'F2' проекциясы түзу ретінде көрсетіледі.
Екінші орын ауыстыруы ΔCDF деңгейдің горизонталь жазықтық жағдайында болатындай етіп жүзеге асырылады. Сонда оның C2''D2''F2'' фронталь проекциясы ОХ өсіне параллель болуы керек. Сол үшін C2'D2'F2' кесіндісі ұзындығын өзгертпей сызбаның бос жеріне көшіріледі. Осыдан ОХ өсіне параллель C2''D2''F2''- ны аламыз. Ал C1', D1', F1' нүктелерінің әр қайсысы ОХ өсіне параллель түзулер бойымен сәйкесінше C2'',D2'',С2'' нүктелерімен байланыс сызықтарына дейін жылжиды.
Осыдан алынған ΔС1''D1''F1'' деңгейдің горизонталь жазықтығының горизонталь проекциясы болғандықтан, ол ΔCDF-ның нақты өлшемі болып есептеледі.
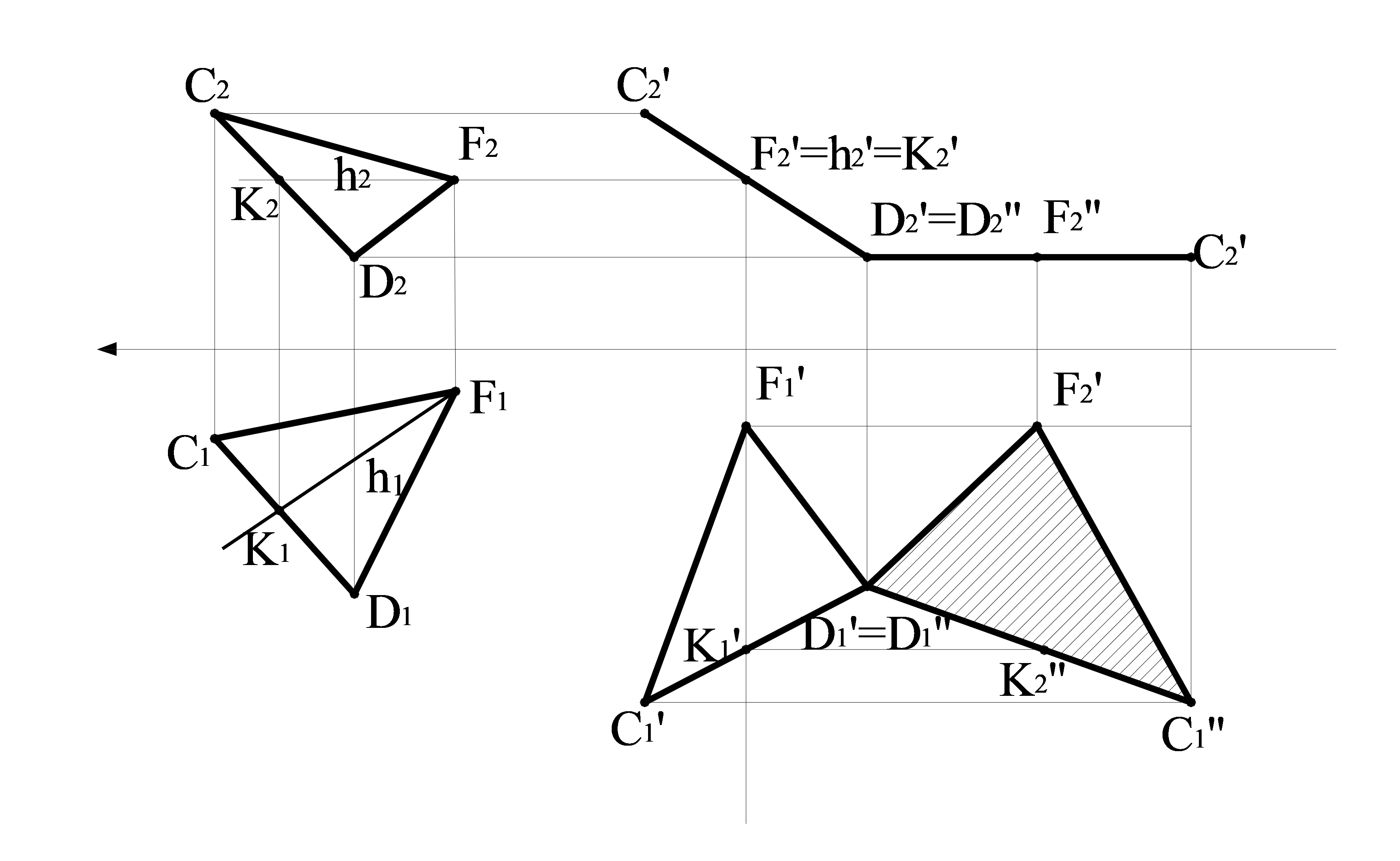
4.4 сурет – Жазықтықтың жазық-параллель орын ауыстыру
4.3 Блок. Проекцияның жазықтықтарын алмастыру тәсілі
Проекциялардың негізгі жазықтықтарының бірі π 1 немесе π 2 жаңа π4 жазықтығымен алмастырылады. Ол жазықтық кескінделген геометриялық нысанға қатысты орналасады, бірақ ол өзгермейтін проекция жазықтығына перепендикуляр болады.
Мысал. Егер π2 жазықтығы алмастырылған болса, онда негізгі жазықтықтарының біреуін π4 проекция жазықтығына алмастыру нәтижесінде проекция жазықтықтарының π1/ π2 ескі жүйесінің орнына жаңа π1/ π4 жүйесін аламыз және егер де π1 жазықтығы алмастырыған болса, π 2/ π 4 жүйесін аламыз (4.5 сурет). Суретте π4 жазықтығы π2 фронталь проекция жазықтығының рөлінде болуы мүмкін. 4.5суретте D нүктесінен π1 проекциясының горизонталь жазықтығына дейінгі ара қашықтық фигуралы сызықтармен белгіленген. Әрине, бұл ара қашықтық D2D12=D4D14-ке тең, сондай-ақ D нүктесінің π1 жазықтығындағы биіктігі π2 –ге де, π 4-ге де бірдей кесінділер түрінде проекцияланады. D нүктесінен π2 және π4 дейінгі ара қашықтық әр түрлі болуы мүмкін, сондықтан D1D12≠D1D14.

4.5 сурет – Проекцияның жазықтықтарын алмастыру тәсілі
Проекция жазықтықтарын алмастыру тәсілін келесілерді анықтау бойынша есептерді шешу кезінде қолданылады:
- түзу сызық кесіндісінің нақты өлшемін анықтауда;
- жазық фигураның нақты өлшемін анықтауда;
- екі қырлы бұрыштың нақты өлшемін анықтауда;
- нүктеден бастап түзу сызыққа дейінгі немесе жазықтыққа дейінгі қысқа қашықтықты анықтауда;
- екі параллель немесе айқасатын түзулер арасындағы қысқа қашықтықты анықтауда.
Берілген тәсіл арқылы есептердің шешілуін бірнеше мысалдар арқылы қарастырайық.
4.3.1 Блок. Жалпы жағдайдағы кесіндісінің ұзындығын анықтау
Жалпы жағдайдағы түзу сызықтың CD кесіндісінің нақты өлшемін анықтау үшін бұл кесіндіні проекция жазықтығының жаңа жүйесінде деңгей сызығы етіп жасау қажет. Ол үшін π 2 жазықтығын CD-ға параллель π 4 жазықтығына ауыстырып, π 1/ π2 жүйесінен π 1/ π4 жүйесіне көшеміз. Х14 проекциясының жаңа өсін C1D1-ге параллель етіп аламыз (4.6 сурет). CD кесіндісінің жаңа проекциясын құру үшін, Х14 өсіне перпендикуляр проекциялық байланыстың жаңа сызықтарын жүргіземіз және оларда C мен D нүктелерінің C4,D4 жаңа проекцияларын белгілейміз. Ол үшін Cх1C4=C2Cx; Dх1 D4 =D2Dх қалдырамыз.
Табылған C4D4 нүктелерін қосып, CD кесіндісінің C4D4 жаңа проекциясын аламыз. Көріп тұрғанымыздай, π1/ π4 проекция жазықтықтарының жүйесіндегі CD кесіндісі деңгейлік сызығы болып табылады, себебі Х14 –ке C1D1 параллель, демек, π4-ке CD параллель. Сонда C4D4 CD кесіндісінің нақты өлшемі екендігі белгілі.
4.3.2 Блок. Жазық фигураның нақты өлшемдерін анықтау
Жазық фигураның нақты өлшемдерін анықтау үшін қосымша жазықтықты қарастырылып отырған фигураға параллель болатындай етіп салу қажет, сонда жазық фигура осы проекция жазықтығына нақты өлшемге проекцияланады. Егерде жазық фигура ретінде үшбұрышты алсақ, онда есеп келесі түрде беріледі: жалпы жағдайдағы үшбұрыш жазықтығын проекция жазықтықтарының жаңа жүйесінде деңгей жазықтығы етіп түрлендіру.
Мысал. Проекция жазықтығын бір рет ауыстырып бұл есепті шешу мүмкін емес, себебі келесі шартты ұстану қажет: жаңа жазықтық ауыстырылмайтын жазықтыққа перпендикуляр болуы керек (4.7 сурет). Сондықтан, бұл есепті екі ауыстырумен шешеміз: бірінші – ΔCDF-ға перпендикуляр болатын жазықтықты, екінші – ΔCDF-ға параллель жазықтықты еңгіземіз.
ΔCDF-ға перпендикуляр π4 жазықтығын құру үшін, оны осы үшбұрыштың фронталына немесе горизонталына перпендикуляр болатындай етіп орналастыру қажет. π4 жазықтығы горизонталға перпендикуляр болсын, сонда Х14 жаңа өсі h1-ге перпендикуляр болуы керек. Оны C1D1F1-ден еркін қашықтықта құрамыз. Сосын C1,D1,F1 нүктелерінен Х14-ке перпендикуляр байланыс сызықтарын жүргіземіз. Олардың әрқайсысында Х14 өсінен, сәйкес нүктенің фронталь проекциясынан Х12 өсіне дейінгі ара қашықтыққа тең, кесінді қалдырамыз. Нәтижесінде, ΔCDF жазықтығы π4 жазықтығына перпендикуляр болғандықтан, CDF үшбұрышының C4D4F4 жаңа проекциясын аламыз, ол түзу ретінде көрсетіледі.
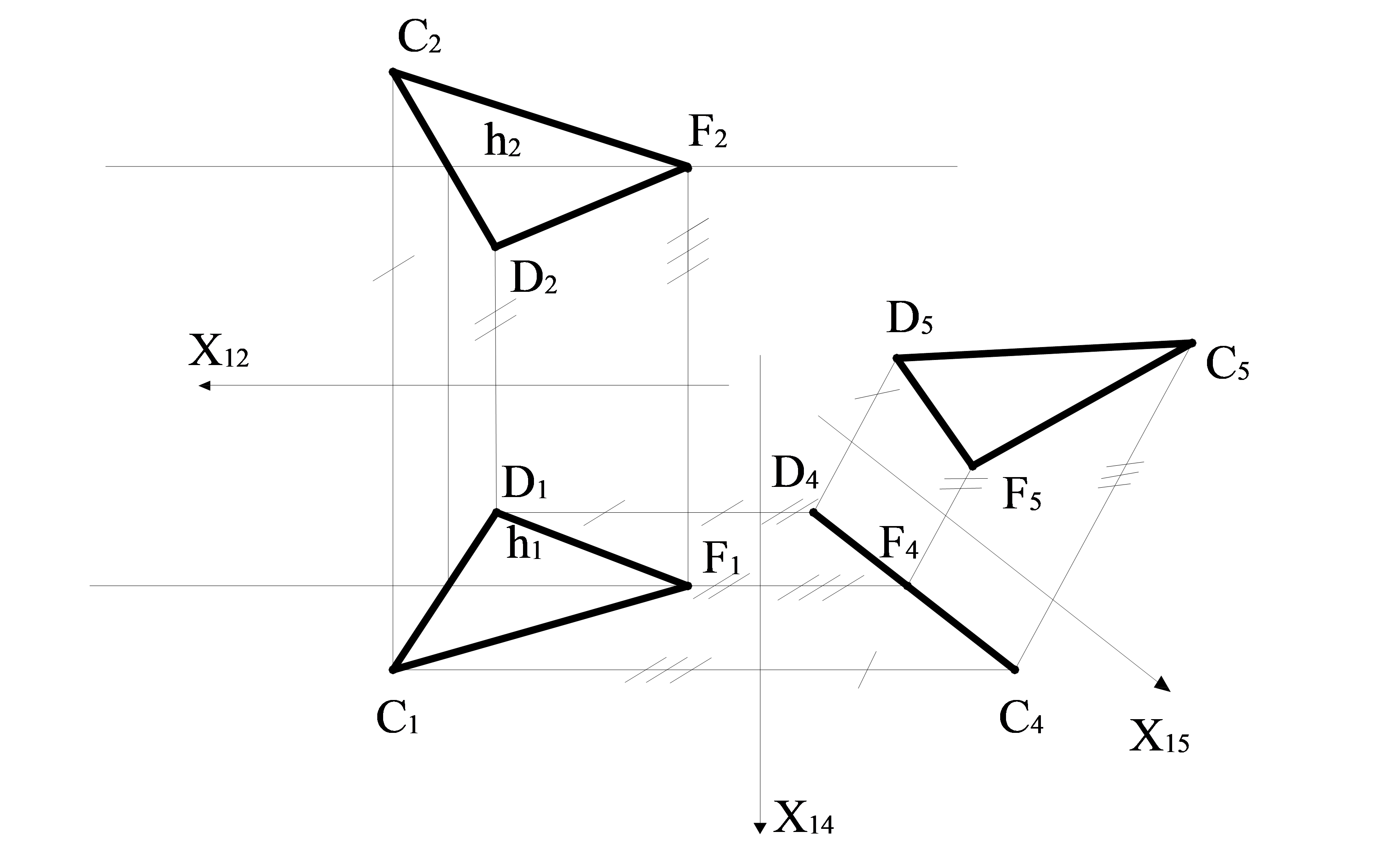
4.7 сурет – Жалпы жағдайдағы жазықтықты денгейлік жазықтыққа айналдыру
Екінші ауыстыру ретінде CDF үшбұрыш жазықтығына параллель π1 жазықтығының орнына π5 жазықтығын аламыз. Сонда Х45 өсі C4D4F4-ке параллель болатын π 4 / π5 проекция жазықтығының жүйесі пайда болады. Ол C4D4F4 –тен еркін ара қашықтықта орналасуы мүмкін. Әрі қарай C4D4F4 нүктелерінен Х45-ке перпендикуляр байланыс сызығын өткіземіз және олардың әр қайсысында сәйкес нүктенің горизонталь проекциясынан Х14 өсіне дейінгі ара қашықтыққа тең кесінді қалдырамыз. C5,D5,F5 нүктелерін аламыз, оларды қосқанда ΔC5D5F5 шығады және де ол Δ CDF-ның нақты өлшемі болып саналады, себебі проекция жазықтығының жаңа жүйесінде ΔCDF үшбұрышы π5 жазықтығына параллель.
4.3.3 Блок. Нүктеден түзуге дейінгі қысқа қашықтықты анықтау>
Нүктеден түзуге дейінгі қысқа қашықтықты, яғни берілген нүктеден түзуге дейінгі жүргізілген перпендикулярдың ұзындығын анықтау үшін, бұл перпендикулярға параллель және берілген түзуге перпендикуляр проекция жазықтығын құрастыру қажет. Демек, түзу осы қосымша проекция жазықтығына қатысты проекцияланып және бұл жазықтыққа нүкте болып проекциялануы керек. Егер жалпы жағдайдағы түзуді берсек, онда бұл проекция жазықтықтарының екі рет ауыстырылуымен жүзеге асуы мүмкін.
Мысал.
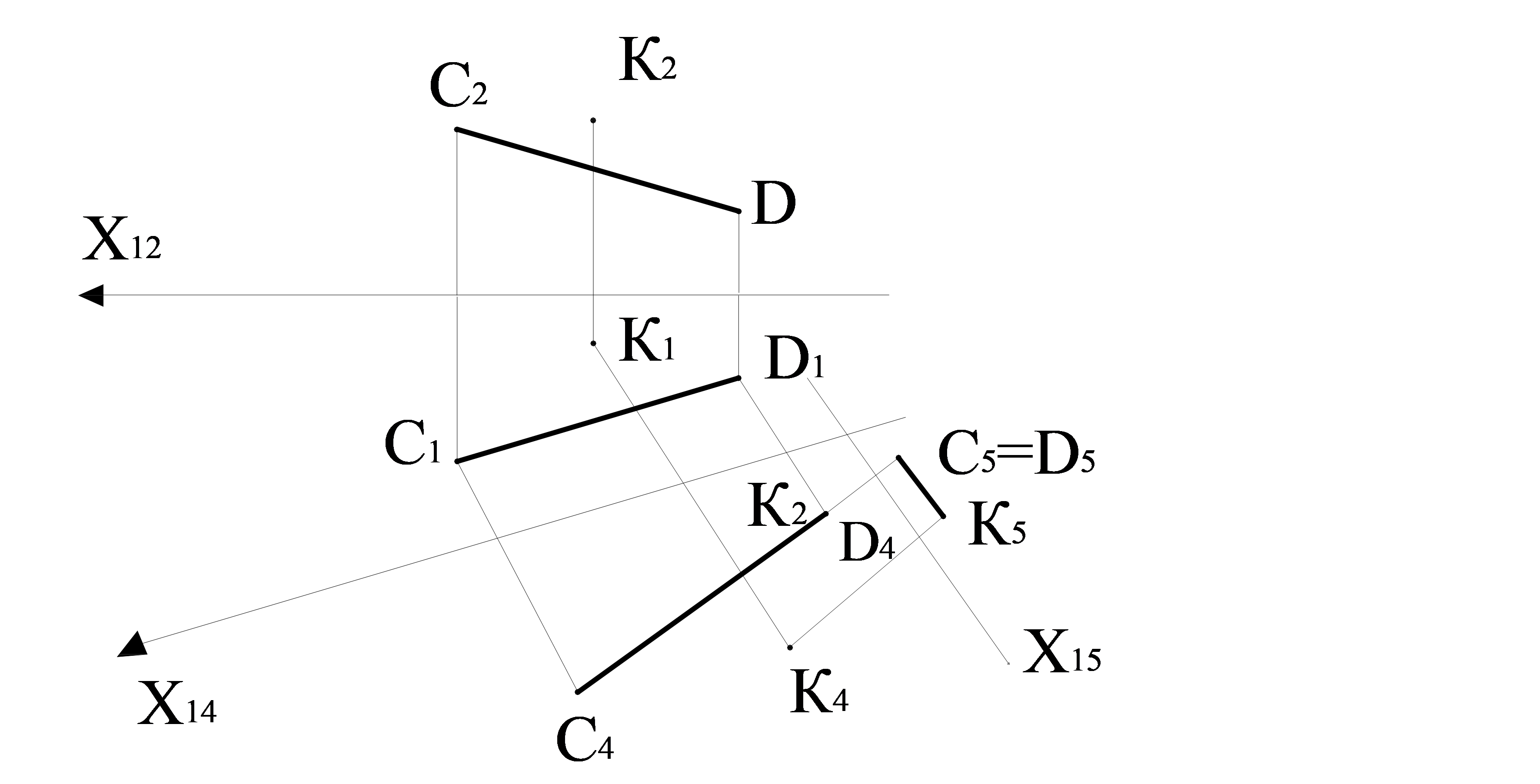
4.8 сурет- А нүктемен СD түзудің арасындағы қашықтығығын табу
K нүктесінен жалпы жағдайдағы СD түзуіне дейінгі ара қашықтықты табу берілсін. Түзуді 4.8 суреттегі тұрғызуға сәйкес проекциялаушы қалпына келтіреміз. Ең алдымен, C1D1-ге параллель Х14 өсін, содан кейін C4D4-ке перпендикуляр Х45 өсін құрамыз. C4 Х14 өсінен C2Х12 өсіне тең алшақтатылған. Өз кезегінде C5 нүктесі Х45 өсінен C1 нүктесі Х14 өсіне дейінгі қашықтығына тең алшақтатылған. C5 және D5 нүктелері бір нүктеге біріккендіктен, C5K5 кесіндісінің ұзындығы CD түзуі мен К нүктесінің арасындағы қысқа қашықтық болып саналады. Осыған ұқсас, жалпы жағдайдағы жазықтық пен нүкте арасындағы қысқа қашықтықты анықтауға арналған есептер шешіледі, мұнда жазықтықты проецияланған жағдайға келтіру үшін проекция жазықтығын бір рет ауыстыруды қолдану жеткілікті. Ал берілген берілген жазықтық жаңа проекция жазықтығында түрленетін, берілген нүктеден түзуге дейінгі перпендикуляр жазықтық пен нүкте арасындағы қысқа қашықтық болып табылады. Егер де жазықтық кеңістікте жалпы жағдайдағы қалпында болса, онда бұл есепті берілген жазықтыққа перпендикуляр болатын проекция жазықтығында қосымша салуларсыз шешуге болады.
4.3.4 Блок. Екі айқасқан түзу арасындағы қысқа қашықтықты анықтау
Бұл есепті шешу үшін екі айқасқан түзудің перпендикулярына параллель жазықтықты құру қажет. Сонымен қатар, бұл қосымша жазықтық берілген түзулердің біреуіне перпендикуляр болуы керек. Егер де түзулер жалпы жағдайда болса, онда есеп проекция жазықтықтарын екі рет ауыстырумен шешіледі.
Мысал. CD және EF түзулерінің арасындағы қысқа қашықтықты анықтау берілсін (4.9 сурет).
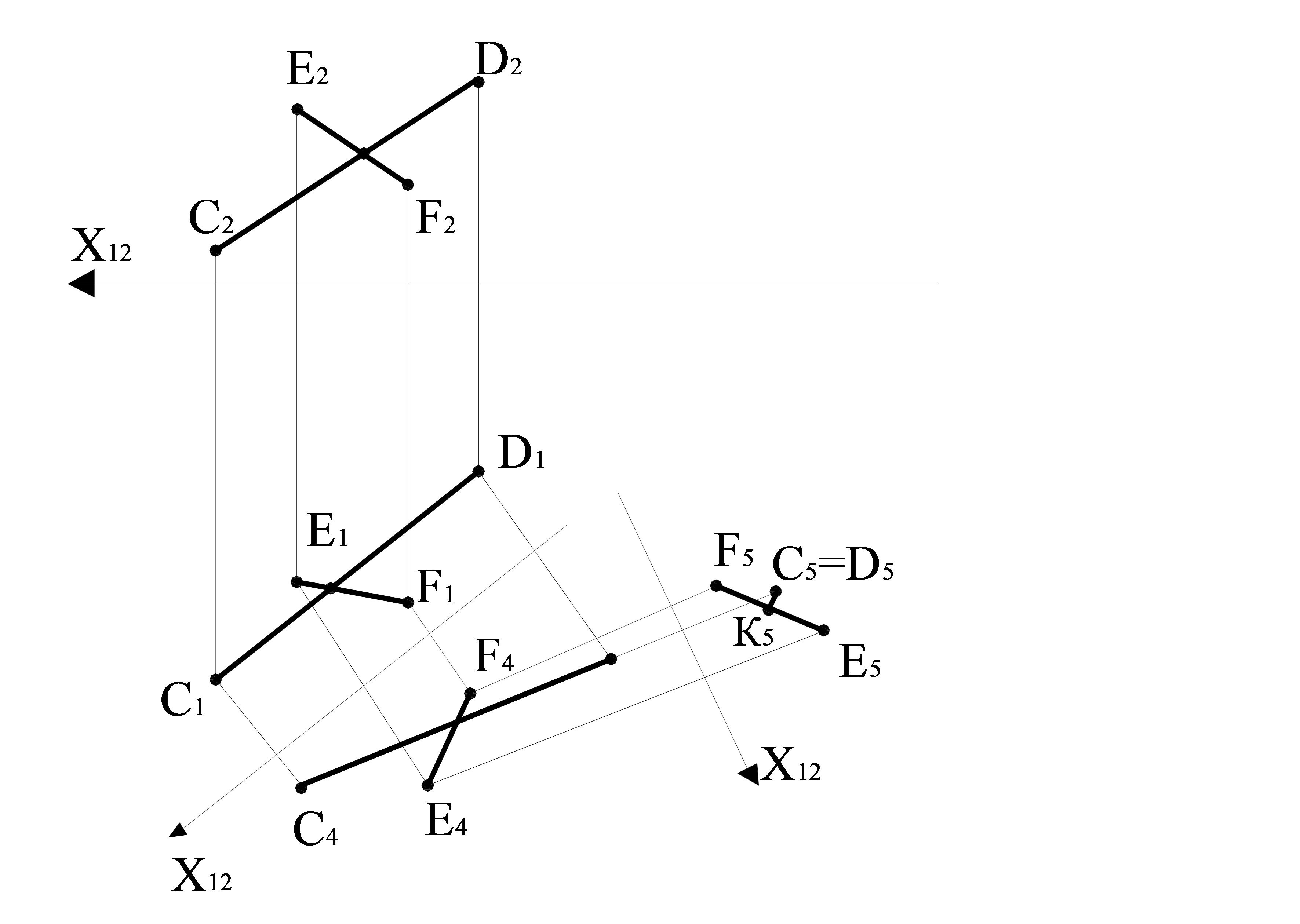
4.9 сурет – CD және ЕF айқасқан түзулердің арасындағы қашықтықты табу
Есептің шешілуі белгілі бір түзуді, мысалы CD түзуін, проециялаушы қалпына келтіру керек. Ол үшін бірінші π4 қосымша жазықтығын CD түзуіне паралель және π1-ге перпендикуляр тұрғызып, ал екінші π5 қосымша жазықтығын СD мен π4-ке перпендикуляр орналастырамыз.
π4 пен π5 жазықтықтарындағы C, D, E және F нүктелерінің барлық проекцияларының салынуы алдыңғы есептерге ұқсас келтіріп құрастырылады. π 5-тегі C5 және D5 проекциялары сәйкес келгендіктен, яғни CD π5-ке қатысты проекциялаушы болады, онда C5 нүктесінен өткізілген E5F5-ке перпендикуляр болатын C5K5 түзуінің кесіндісінің ұзындығы CD мен EF түзулерінің арасындағы қысқа қашықтық болып саналады.
Егер де берілген түзулердің біреуі дербес жағдайда болса, онда есептің шешілуі жеңілдетіледі.
Екі параллель түзулер арасындағы қысқа қашықтық сәйкес түрде шығарылады: ең алдымен, берілген түзулерге параллель жаңа проекция жазықтығын, содан кейін оларға перпендикуляр түрде саламыз. Сонда проекция жазықтықтарын екінші рет ауыстырғаннан кейін берілген түзулер нүктелер түрінде проекцияланады және бұл нүктелерді қосатын түзудің ұзындығы өзара параллель түзулер арасындағы қысқа қашықтық болады.
Демек, кең ауқымды есептерді шешуге мүмкіндік беретін проекция жазықтықтарын ауыстыру тәсілі салудың қарапайымдылығының көрнекілігін біріктіретін кең тараған және әмбебап тәсілдердің бірі болып саналады.
Ұсынылған теориялар төмендегі жағдайларға негізделеді:
1) сызбаны түрлендіру тәсілдері геометриялық нысандардың нақты өлшемдерін немесе геометриялық нысандардың арасындағы қысқа ара қашықтықты анықтайтын метрлік есептерді шешу үшін қолданылады;
2) кешенді сызбаны түрлендіру екі негізгі тәсілмен жүзеге –асырылады:
- айналдыру тәсілі. Мұнда проекция жазықтығы жүйесін өзгеріссіз қалдырады, ал берілген геометриялық нысанның қалпын біз қарастырып отырған жазықтық немесе түзу проекция жазықтығының біріне параллель болатындай етіп бір немесе таңдалған екі өстің айналасында айналдыру жолымен өзгертеді;
- проекция жазықтықтарын алмастыру тәсілі. Бұл тәсілде кеңістіктегі геометриялық нысаннның орналасуын өзгеріссіз қалдырып, ал бізге қажет түзулер немесе жазықтықтар проекцияның жаңа жазықтықтарының біреуіне параллель болатын етіп, бір немесе тізбектей екі проекция жазықтығын алмастырады;
3) Проекциялардың негізгі жазықтықтарының бірі π 1 немесе π 2 жаңа π4 жазықтығымен ауыстырылады. Ол жазықтық кескінделген геометриялық нысанға қатысты орналасады, бірақ ол өзгермейтін проекция жазықтығына перепендикуляр болады.
4) Проекция жазықтықтарын ауыстыру тәсілін келесілерді анықтау бойынша есептерді шешу кезінде қолданылады:
- түзу сызық кесіндісінің нақты өлшемін анықтауда;
- жазық фигураның нақты өлшемін анықтауда;
- екі қырлы бұрыштың нақты өлшемін анықтауда;
- нүктеден бастап түзу сызыққа дейінгі немесе жазықтыққа дейінгі қысқа қашықтықты анықтауда;
- екі параллель немесе айқасатын түзулер арасындағы қысқа қашықтықты анықтауда;
5) жалпы жағдайдағы түзу сызықтың кесіндісінің нақты өлшемін анықтау үшін бұл кесіндіні проекция жазықтығының жаңа жүйесінде деңгей сызығы етіп жасау қажет;
6) жазық фигураның нақты өлшемдерін анықтау үшін қосымша жазықтықты қарастырылып отырған фигураға параллель болатындай етіп салу қажет, сонда жазық фигура осы проекция жазықтығына нақты өлшемге проекцияланады. Егерде жазық фигура ретінде үшбұрышты алсақ, онда есеп келесі түрде беріледі: жалпы жағдайдағы үшбұрыш жазықтығын проекция жазықтықтарының жаңа жүйесінде деңгей жазықтығы етіп түрлендіру.
7) нүктеден түзуге дейінгі қысқа қашықтықты, яғни берілген нүктеден түзуге дейінгі жүргізілген перпендикулярдың ұзындығын анықтау үшін, бұл перпендикулярға параллель және берілген түзуге перпендикуляр проекция жазықтығын құрастыру қажет.
Тапсырма.
1 есеп. Кеністікте жалпы жағдайдағы СD түзудең A нүктеге дейінгі қашықтықты анықтау қажет (4.10 cурет)
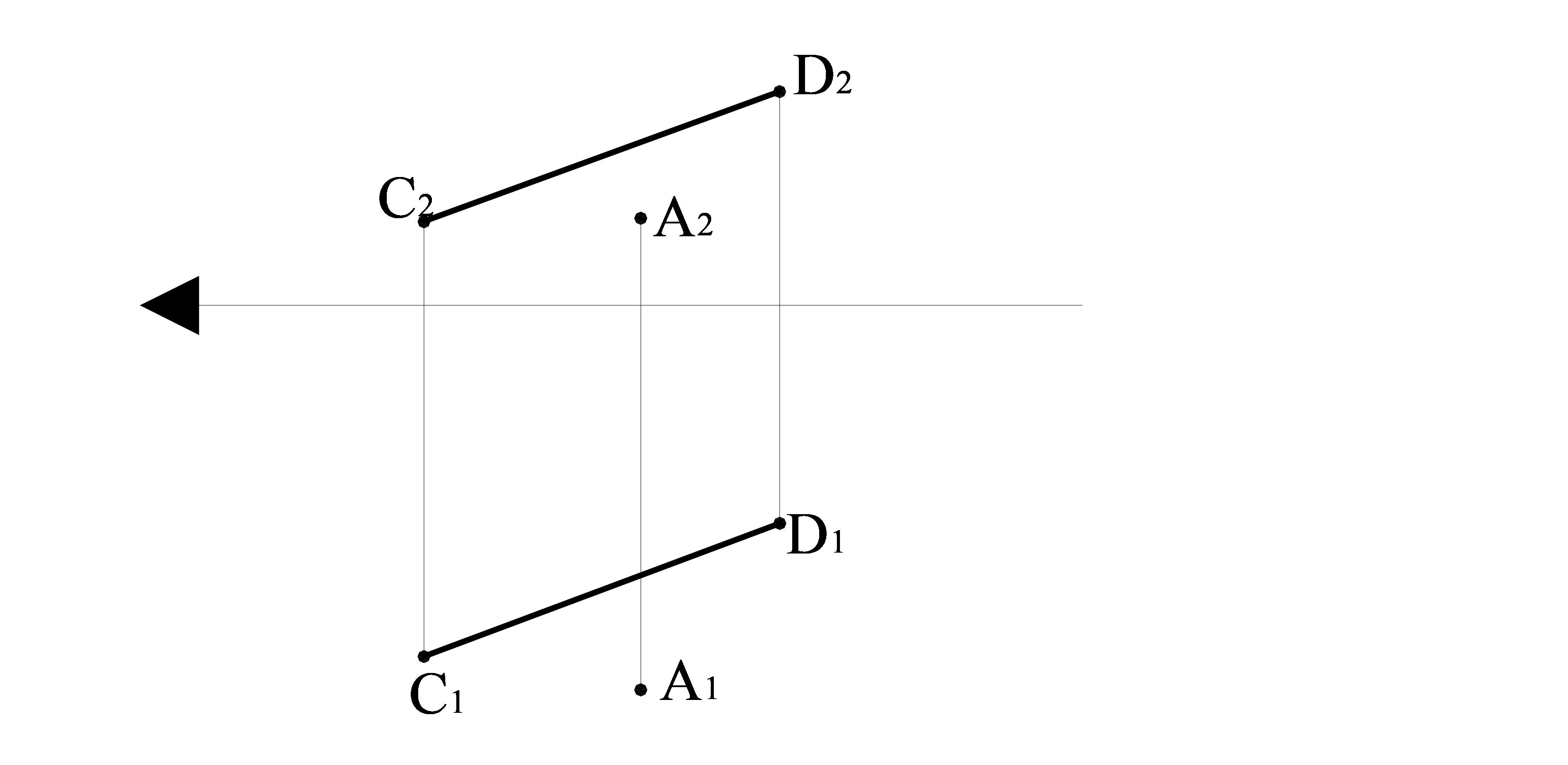
4.10 cурет
2 есеп. ΔАВС жазықтығының нақты өлшемін анықтау қажет (4.11 cурет).
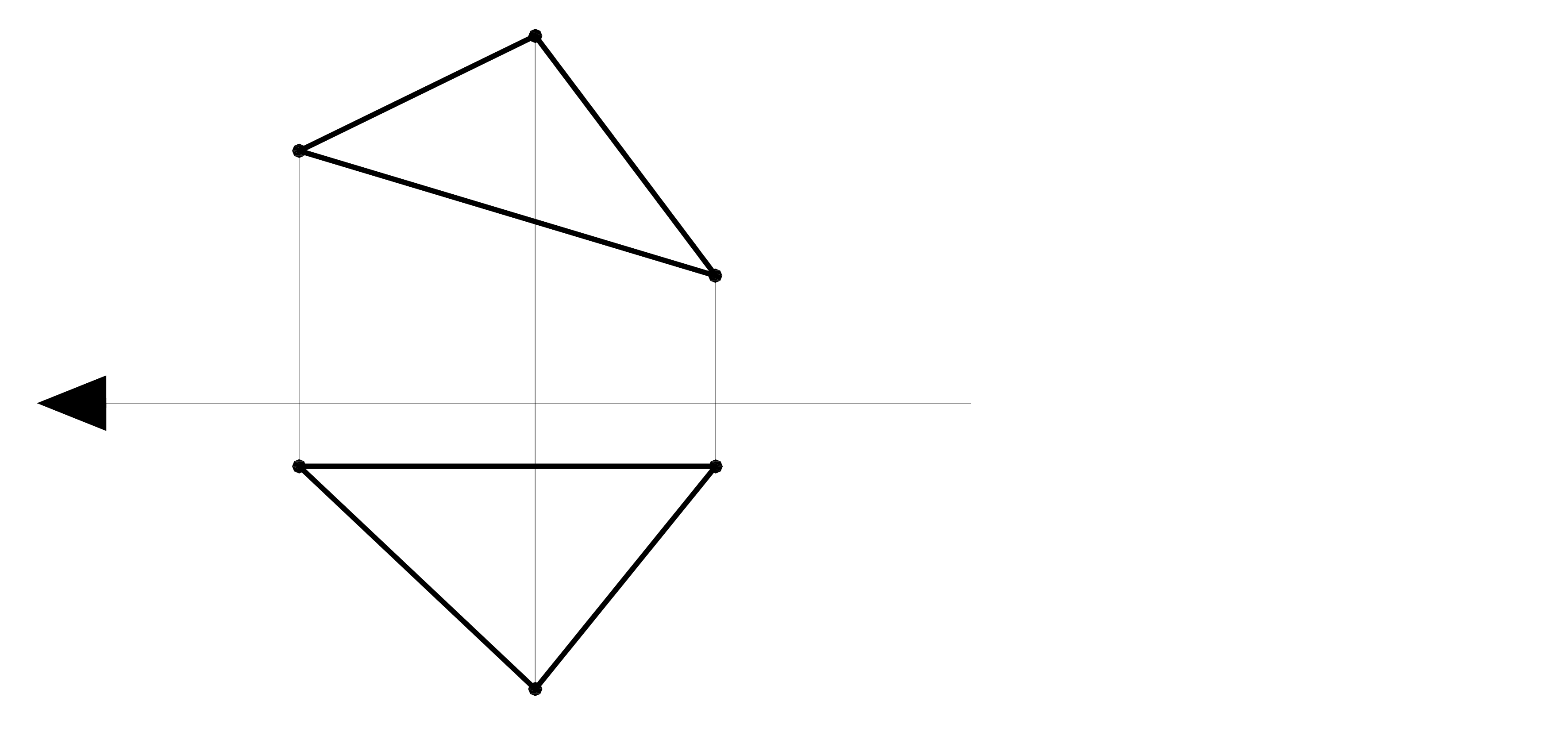
4.11сурет
Өзіндік талдау үшін сұрақтар:
- Проекция жазықтықтарын алмастыру тәсілі не үшін қажет?
- Проекция жазықтықтарын алмастыру тәсілінің ерекшіліктері?
- Жазық апараллель орын ауыстыру тәсілі не үшін қажет?
- Айналу өсі проекция жазықтығына қалай орналасады?
- Кешенді сызбаны түрлендіру қанша тәсілмен шешуге болады?
- Үшбұрышпен берілген жазықтықтың нақты өлшемін табу үшін қай тәсілді қолдануға қолайлы?
- Кесіндінің нақты өлшемің табу үшін қандай тәсіл колданады?
- Берілген өстен айналдыра бұру тәсілінің ерекшілігі қандай?
Бақылау жұмысы
1 есеп. СD түзуін профиль проекциялаушы жағдайға келтіру қажет (4.12а сурет).
2 есеп. Жалпы жағдайдағы үшбұрышымен берілген жазықтықтың нақты өлшемін табу қажет (4.12б сурет).
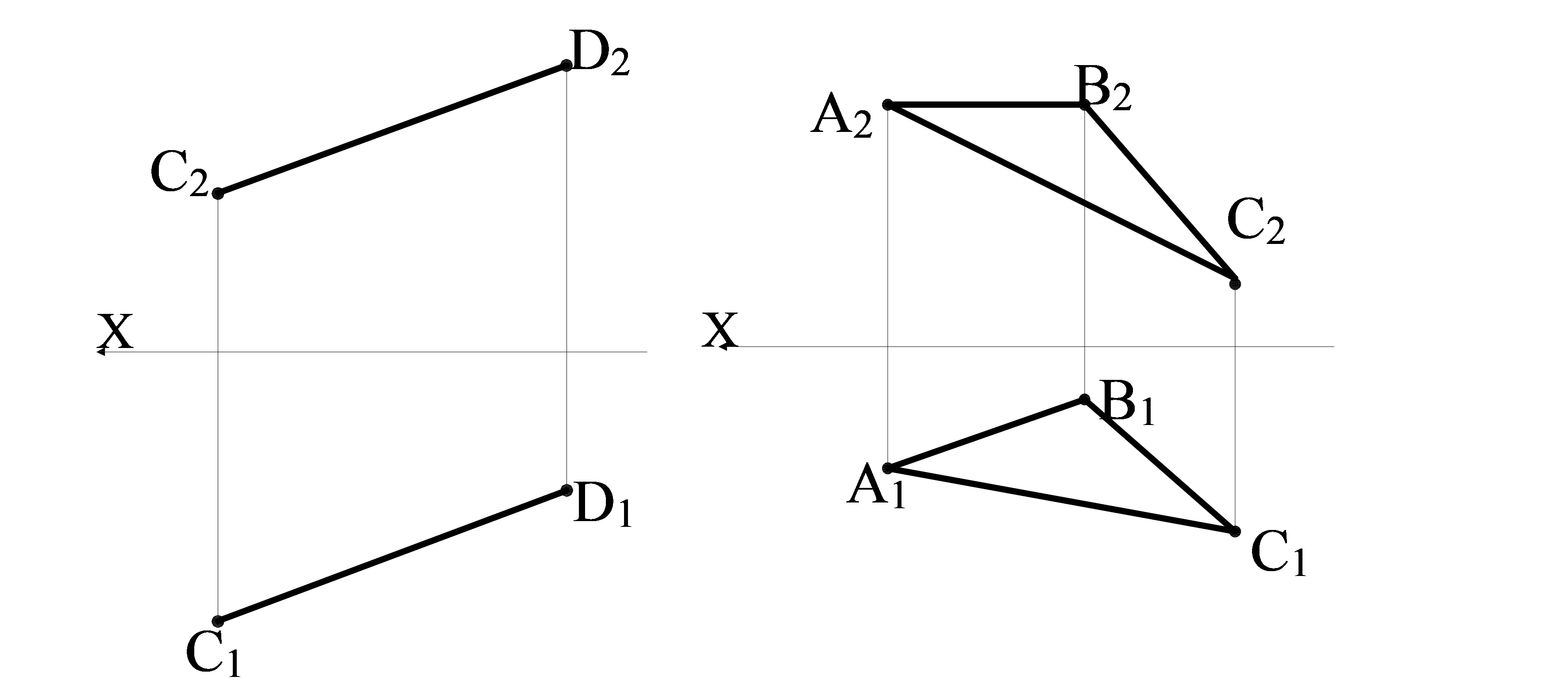
4.12 сурет