Практическая работа 10. Линейная алгоритмическая конструкция. Разветвляющая алгоритмическая конструкция. Рекурсивный алгоритм. Блок-схемы (элементы блок-схем, типы блоков).

Алгоритм – это точное предписание, определяющее вычислительный процесс, ведущий от варьируемых начальных данных к исходному результату

Центральным объектом в этой системе является ИСПОЛНИТЕЛЬ алгоритмов. Исполнитель – это тот объект (или субъект), для управления которым составляется алгоритм. Основной характеристикой исполнителя, с точки зрения управления, является система команд исполнителя. Это конечное множество команд, которые понимает исполнитель, т.е. умеет их выполнять.

Для выполнения всякой работы, решения поставленной задачи исполнитель на входе получает алгоритм и исходные данные, а на выходе получаются требуемые результаты

При составлении алгоритмов следует учитывать ряд требований, выполнение которых приводит к формированию необходимых свойств:

1. алгоритм должен быть однозначным, исключающим произвольность толкования любого из предписаний, и заданного порядка исполнения. Это свойство алгоритма называется определенностью (детерминированностью);
2. реализация вычислительного процесса, предусмотренного алгоритмом, должна через определенное число шагов привести к выдаче результатов или сообщения о невозможности решения задачи. Это свойство алгоритма называется результативностью;
3. решение однотипных задач с различными исходными данными можно осуществлять по одному и тому же алгоритму, что дает возможность создавать типовые программы для решения различных вариантах задания значений исходных данных. Это свойство алгоритма называется массовостью;
4. предопределенный алгоритмом вычислительный процесс можно расчленить на отдельные этапы, элементарные операции. Это свойство алгоритма называется дискретностью.

Так как алгоритм является совокупностью предписаний по выполнению действий, то всегда необходимо выделить объекты, над которыми должны осуществляться предписанные действия. Такими объектами являются данные.

Конечность алгоритма означает, что он должен выполняться за конечное время.

Таким образом, алгоритм дает возможность чисто механически решать любую конкретную задачу из некоторого класса однотипных задач и предполагает наличие определенных свойств:

• алгоритм состоит из отдельных шагов;
• каждый шаг выполняет обработку входных данных (аргументов), получая выходные данные (результаты);
• результат каждого шага однозначно определяется аргументами;
• количество шагов конечно;
• шаги алгоритма выполняются последовательно, в порядке написания (естественный порядок выполнения);
• существуют способы изменения естественного порядка выполнения (управляющие конструкции).

С понятием алгоритма тесно связано понятие «данные». В алгоритмическом аспекте данные  это информация, несущая полезную смысловую нагрузку, представленная в формализованном виде, позволяющем собирать, передавать, вводить и обрабатывать эту информацию с помощью заданных алгоритмов. Реализация алгоритма на конкретных исходных данных решаемой задачи называется алгоритмическим процессом.

Существует несколько способов описания алгоритмов: словесный, формульно-словесный, графический, средствами специального языка операторных схем, с помощью таблиц решений и др. Помимо требования обеспечения наглядности, выбор конкретного способа диктуется рядом факторов, из которых определяющими являются степень необходимой детализации представления алгоритма, степень его формализации, уровень логической сложности задачи и т.п.

Словесный способ описания алгоритма основан на записи содержания выполняемых действий средствами естественного языка. К достоинствам этого способа следует отнести его общедоступность, возможность описывать алгоритм с любой степенью детализации, а к главным недостаткам - довольно громоздкое описание (и как следствие - относительно низкую наглядность), отсутствие строгой формализации в силу неоднозначности восприятия естественного языка, вытекающего из свойств синонимии, омонимии, полисемии.

Формульно-словесный способ описания алгоритма основан на записи содержания выполняемых действий с использованием изобразительных возможностей языка математики, дополненного - с целью указания необходимых пояснений - средствами естественного языка. Обладая всеми достоинствами словесного способа, формульно-словесный способ вместе с тем более лаконичен, а значит, и более нагляден, имеет большую формализацию, однако также не является строго формальным.

Графический способ описания алгоритма  это такое изображение логико-математической структуры алгоритма, при ко¬тором все этапы процесса обработки данных представляются с помощью определенного набора геометрических фигур (блоков), имеющих строго определенную конфигурацию в соответствии с характером выполняемых действий.

Каждый алгоритм должен задаваться:

• множеством допустимых исходных данных;
• начальным состоянием;
• множеством допустимых промежуточных состояний;
• правилами перехода из одного состояния в другое;
• множеством конечных результатов;
• конечным состоянием.

В зависимости от конкретного задания этих параметров определяются классы алгоритмов, например алгоритмы линейные, циклические, сортировки и т. д.

В зависимости от исполнителя, алгоритм может запи¬сываться с помощью графических обозначений – блок-схем.

Разработка блок-схем алгоритмов

Для решения задачи на ПЭВМ должна быть составлена программа. Составлению программы предшествует процесс разработки, так называемой логической схемы программы. Под логической схемой программы понимают условную (символическую) запись, показывающую последовательность выполнения отдельных этапов программы при решении задачи.

Для программ в языках программирования при их выполнении характерно строго последовательное выполнение содержащихся в них указаний (операторов). Какой оператор в зависимости от обстоятельств должен выполниться в качестве следующего, управляется через специальные условия. Переход от одного оператора к другому в процессе выполнения программы называется течением программы (управлением потоком). Наиболее наглядный способ представления алгоритмов – их изображение в виде схем – последовательности блоков, предписывающих выполнение определенных функций и связей между ними. Внутри блока указывается поясняющая информация, характеризующая выполняемые ими действия.

Блок-схемы имеют свои недостатки: в сложных программах преимущества наглядного представления управления потоком теряются. Обычно блок-схемы применяют для несложных программ, содержащих условные операторы и операторы цикла, т.е. алгоритмов линейной, разветвляющейся и циклической структуры.

Для изображения структур алгоритмов используется совокупность блочных символов (блоков), соединяемых линиями передач управления.

В схеме алгоритма каждому типу действий (вводу исходных данных, вычислению значений выражений, проверке условий, управлению повторением действий, окончанию обработки и т.п.) соответствует геометрическая фигура, представленная в виде блочного символа (блока), называемая символом действия. Символы действия соединяются линиями переходов, определяющими очередность выполнения действий (таблица 4.1).

Таблица 6.1

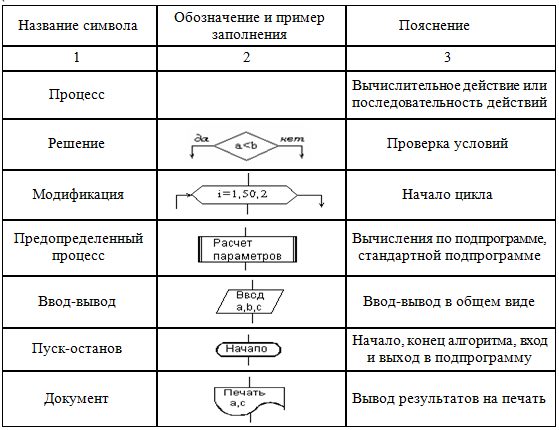
По структуре выполнения алгоритмы и программы делятся на три вида: линейные, разветвленные, циклические.

В зависимости от исполнителя, алгоритм может запи¬сываться с помощью графических обозначений – блок- схем.

Линейный алгоритм (линейная структура) – это такой алгоритм, в котором все действия выполняются последовательно друг за другом и только один раз. Схема представляет собой последовательность блоков, которые располагаются сверху вниз в порядке их выполнения. Первичные и промежуточные данные не оказывают влияния на направление процесса вычисления.

Алгоритмы линейной структуры

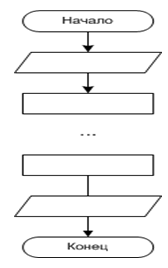
Рисунок 6.1 - Размещение блоков в линейном алгоритме

ПРИМЕР 1. Зная длины трех сторон треугольника, вычислить площадь и периметр треугольника. Пусть a, b, c - длины сторон треугольника. Необходимо найти S - площадь треугольника, P - периметр.

Для нахождения площади можно воспользоваться формулой Герона:		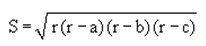где r - полупериметр
Входные данные: a, b, c Выходные данные: S, P.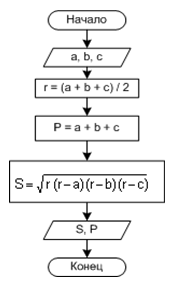

Примечание: В этих блоках знак "=" означает не математическое равенство, а операцию присваивания. Переменной, стоящей слева от оператора, присваивается значение, указанное справа. Причем это значение может быть уже определено или его необходимо вычислить с помощью выражения. Например, операция r = (a + b + c) / 2 - имеет смысл (переменной r присвоить значение r = (a + b + c) / 2), а выражение (a + b + c) / 2= r - бессмыслица.

Алгоритмы разветвленной структуры

На практике часто встречаются задачи, в которых в зависимости от первоначальных условий или промежуточных результатов необходимо выполнить вычисления по одним или другим формулам. В таких алгоритмах выбор направления продолжения вычисления осуществляется по итогам проверки заданного условия. Ветвящиеся процессы описываются оператором IF (условие ЕСЛИ). В блок-схемах разветвленные алгоритмы изображаются так, как показано на (рисунок 6.2).

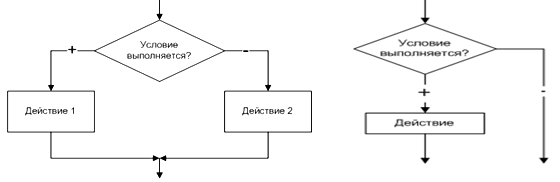
Рисунок 6.2 - разветвлённые алгоритмы

ПРИМЕР 2. Заданы коэффициенты a, b и с биквадратного уравнения ах⁴ + bх² + с = 0. Решить уравнение.

Для решения биквадратного уравнения необходимо заменой y = x² привести его к квадратному и решить это уравнение.

Входные данные: a, b, c. Выходные данные: х₁, х₂, х₃, х₄.

Алгоритм состоит из следующих этапов:

1. Вычисление дискриминанта уравнения d;
2. Если d > = 0, определяются y₁ и y₂, а иначе корней нет;
3. Если y₁, y₂ < 0 , то корней нет;
4. Если y₁, y₂ = 0 , то вычисляются четыре корня по формулам (6.а) и выводятся значения корней.

±√y₁,±√y₂   (6.a)

5. Если условия 3) и 4) не выполняются, то необходимо проверить знак y₁. Если y₁ > = 0, то вычисляются два корня по формуле (6. б). Если же y₂ > = 0, то вычисляются два корня по формуле (6. с) Вычисленные значения корней выводятся.

±√y₁(6.б)   ±√y₂(6.с)

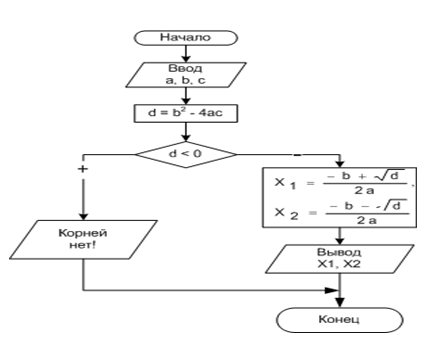
Рисунок 6.3 - Блок-схема алгоритма решения квадратного уравнения

Алгоритм циклической структуры

Алгоритм циклической структуры (циклический алгоритм) – алгоритм, в котором выполняемая последовательность действий повторяется многократно при различных значениях входящих в них величин. Многократно повторяющиеся участки называются циклами (рисунок 4.4).

Для организации цикла необходимо:

1. Задать начальное значение параметра цикла;
2. После выполнения цикла изменить значение параметра цикла;
3. Проверить условие выхода из цикла.

Особенностью первой схемы является то, что проверка условия выхода из цикла проводится до выполнения тела цикла. В том случае, если условие выхода из цикла выполняется, то тело цикла не выполняется ни разу.

Особенностью второй схемы является то, что цикл выполняется хоты бы один раз, так как первая проверка условия выхода из цикла осуществляется после того, как тело цикла выполнено.

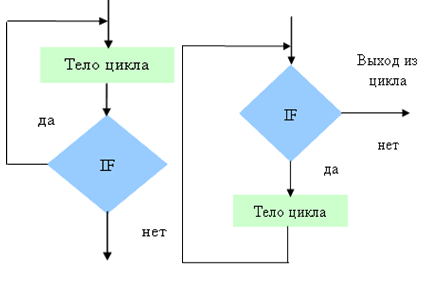
Рисунок 6.4 - Алгоритм циклической структуры

ПРИМЕР 3. Вычислить aⁿ (n > 0).

Входные данные: a - вещественное число, которое необходимо возвести в целую положительную степень n.

Выходные данные: p (вещественное число) - результат возведения вещественного числа a в целую положительную степень n.

Промежуточные данные: i - целочисленная переменная, принимающая значения от 1 до n с шагом 1, параметр цикла.

Блок-схема приведена на рисунок 6.5.

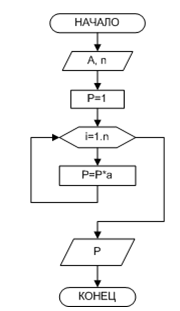
Рисунок 6.5 - Возведение вещественного числа в целую степень