Практическая работа 9. Архитектура компьютера. Хранение информации. Системы счисления.
Системой счисления называется совокупность приемов наименования и записи чисел. В любой системе счисления для представления чисел выбираются некоторые символы (слова или знаки), называемые базисными числами, а все остальные числа получаются в результате каких-либо операций из базисных чисел данной системы счисления. (В двоичной системе счисления используются всего две цифры 0 и 1. Другими словами, двойка является основанием двоичной системы счисления. Аналогично у десятичной системы основание 10). Система называется позиционной, если значение каждой цифры (ее вес) изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображаю¬щих число. Если это условие не выполняется, то система счисления является непозиционной (например, римская).
| Десятичная система | Двоичная система | Шестнадцатеричная система |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 10 | 2 |
| 3 | 11 | 3 |
| 4 | 100 | 4 |
| 5 | 101 | 5 |
| 6 | 110 | 6 |
| 7 | 111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | E |
Число единиц какого-либо разряда, объединяемых в единицу более старшего разряда, называют основанием позиционной системы счисления. Если количество таких цифр равно P, то система счисления называется P-ичной. Основание системы счисления совпадает с количеством цифр, используемых для записи чисел в этой системе счисления.
Запись произвольного числа x в P-ичной позиционной системе счисления основывается на представлении этого числа в виде многочлена x = anPn + an-1Pn-1 + ... + a1P1 + a0P0 + a-1P-1 + ... + a-mP-m
Правила перевода.
При переводе чисел из десятичной системы счисления в систему с основанием Р>1 обычно используют следующий алгоритм:
- если переводится целая часть числа, то она делится на Р, после чего запоминается остаток от деления. Полученное частное вновь делится на Р, остаток запоминается. Процедура продолжается до тех пор, пока частное не станет равным нулю. Остатки от деления на Р выписываются в порядке, обратном их получению;
- если переводится дробная часть числа, то она умножается на Р, после чего целая часть запоминается и отбрасывается. Вновь полученная дробная часть умножается на Р и т.д. Процедура продолжается до тех пор, пока дробная часть не станет равной нулю. Целые части выписываются после двоичной запятой в порядке их получения. Результатом может быть либо конечная, либо периодическая двоичная дробь. Поэтому, когда дробь является периодической, приходится обрывать умножение на каком-либо шаге и довольствоваться приближенной записью исходного числа в системе с основанием Р;
- При переводе чисел из системы счисления с основанием Р в десятичную систему счисления необходимо пронумеровать разряды целой части справа налево, начиная с нулевого, и дробной части, начиная с разряда сразу после запятой, слева направо (начальный номер 1). Затем вычислить сумму произведений соответствующих значений разрядов на основание системы счисления в степени, равной номеру разряда. Это и есть представление исходного числа в десятичной системе счисления;
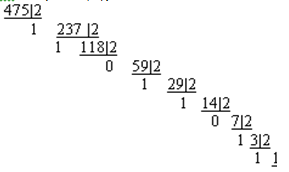
Например. Перевести данное число из десятичной системы счисления в двоич¬ную 475,1875(10);
 | 0,1875*2=0,37 |
| 0,375*2=0,75 |
| 0,75*2=1,5 |
| 0,5*2=1,0 |
| 0,1875=0,00112 |
Читая остатки от деления снизу вверх, получим 111011011. Ответ 111011011,00112
Проверка (обратный перевод):
1*28+1*27+1*26+0*25+1*24+1*23+0*22+1*21+1*20+2*2-1+0*2-2+1*2-3+1*2-4=1+2+8+6+128+256+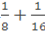
=475,187510
Для перевода двоичного целого числа в восьмеричное двоичное число нужно разбить на группы по три цифры, справа налево; если в последней группе окажется меньше чем три разряда, то необходимо её дополнить слева нулями. Затем надо преобразовать каждую группу в восьмеричную цифру.
Например 1000110 = 1 000 110 = 1068
Для перевода дробного двоичного числа в восьмеричное нужно разбить двоичное число на триады, слева направо; если в последней группе окажется меньше чем три разряда, то необходимо дополнить её справа нулями. Затем надо триады заменить на восьмеричные цифры
Пример 111100101,01112 =111 100 101,011 1002 = 745,348.0,101 0012 = 0,518
Для перевода двоичного числа в шестнадцатеричное двоичное число нужно разбить на группы по четыре цифры (тетрады).
Для перевода двоичного целого числа в шестнадцатеричное двоичное число нужно разбить на группы по четыре цифры (тетрады), справа налево; если в последней группе окажется меньше чем четыре разряда, то необходимо её дополнить слева нулями. Затем надо преобразовать каждую группу в шестнадцатеричную цифру.
Пример 11101001000,11010012 = 0111 0100 1000,1101 00102 = 748,D216
Для перевода из восьмеричной системы в двоичную каждую цифру числа надо преобразовать в группу из трех двоичных разрядов (триаду), а при преобразовании шестнадцатеричного числа – в группу из четырех разрядов (тетраду).
0,478 = 0,1001112
| Таблицы для перевода |
| Двоичная СС | Шестнадцатеричная
СС | | Двоичная СС | Шестнадцатеричная
СС |
| 0000 | 0 | | 000 | 0 |
| 0001 | 1 | | 001 | 1 |
| 0010 | 2 | | 010 | 2 |
| 0011 | 3 | | 011 | 3 |
| 0100 | 4 | | 100 | 4 |
| 0101 | 5 | | 101 | 5 |
| 0110 | 6 | | 110 | 6 |
| 0111 | 7 | | 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
Арифметические операции, выполняемые в позиционных системах счисления
В вычислительной технике наиболее часто выполняется операция сложения. Пусть заданы два целых положительных числа в позиционной системе счисления с основанием р. Запишем эти числа в виде:
A=anpn+an-1pn-1+...+a1p1+a0p0
B=bnpn+bn-1pn-1+...+b1p1+b0p0
S=snpn+sn-1pn-1+...+s1p1+s0p0
Сумма этих чисел равна числу, которое может быть записано в аналогичном виде:
Вычисления выполняются по следующим правилам: операция сложения выполняется поразрядно, начиная с младших разрядов в слагаемых;
- в каждом одноименном разряде слагаемых суммируются соответствующие цифры и перенос из предыдущего разряда суммы;
- если сумма цифр одноименных разрядов слагаемых и переноса меньше основания системы счисления, то перенос в следующий разряд равен нулю, если равна или больше - то равен единице.
В качестве примера рассмотрим арифметические операции в двоичной системе счисления.
Арифметические операции над числами в двоичной системе Счисления
| Правила сложения | | Правила вычитания | | Правила умножения |
| 0 + 0 = 0 | | 0 - 0 = 0 | | 0 * 0 = 0 |
| 0 + 1 = 1 | | 0 - 1 = -1 | | 1 * 0 = 0 |
| 1 + 0 = 1 | | 1 - 0 = 1 | | 0 * 1 = 0 |
| 1 + 1 = 10 | | 1 - 1 = 0 | | 1 * 1 = 1 |
Рассмотрим правила выполнения арифметических операций над однозначными числами. Представим их в виде таблиц.
Примеры. Сложить два числа: 1010(2)+ 10101(2) = 11111(2)2. Найти разность двух чисел 10101(2) и 1010(2):10101(2) - 1010(2) = 1011(2)3. Умножить два числа 1011(2) и 101(2):1011(2) * 101(2) = 110111(2)