Практическая работа 8. Булева алгебра. Логические операции. Формулы и их преобразование.
В 1847 г. английский математик Джордж Буль (1815 - 1864) создал универсальный логический язык. Буль разработал ис¬числение высказываний «булевой алгеброй», которое представляет собой формальную логику, переведенную на строгий язык математики. Пользуясь этой системой, можно закодировать любые утверждения, истинность или ложность которых нужно доказать, а затем манипулировать ими, подобно обычным числам в математике.
Объект рассмотрения в алгебре логики - так называемые высказывания, т. е. любые утверждения, о которых можно сказать, что они либо истинны, либо ложны. Например: «Павлодар - город в Казахстане», «9 - четное число»; первое высказывание истинно, а второе - ложно.
Таким образом, высказывание это любое утверждение, которое может быть либо истинным, либо ложным, но не может быть истинным и ложным одновременно. В математической логике понятие «высказывание» определяется как повествовательное предложение. В информатике это понятие сужается до определения: высказывание это логическое выражение. Над высказываниями возможны определенные операции.
Булева алгебра частный случай алгебры логики.
Основные логические операции
Из простых логических высказываний образовываются сложные высказывания. Для этого используются союзы: И; ИЛИ; ЕСЛИ...ТО; НЕ. Истинное значение высказывания, полученного с помощью более простых высказываний, полностью определяется истинными значениями исходных высказываний. Поэтому каждой логической операции соответствует функция, принимающая значения 1 или 0, аргументы которой также принимают значения 1 или 0. Такие функции и называются логическими функциями.
Рассмотрим основные логические операции.
Инверсией (отрицания) А называют высказывание A̅ которое ложно, когда А истинно, и истинно, когда А ложно. Обозначение отрицания: 1) ¬ A (читается: не А); 2)частица НЕ. Например, А – «Я выполнил домашнее задание», отрицание A̅ будет «Я НЕ выолнил домашнее задание».
Конъюнкция (логическим умножением) двух высказываний А и В является новое высказывание С, которое истинно тогда и только тогда, когда истинны оба высказывания А и В. Обозначение конъюнкции: 1) С=А ∧ В (при этом говорят С равно А и В); 2) символ «•»; 3) &; 4) союз И.
Например « Число 6 делится на 2 и 3»
Дизъюнкция (логическим сложением) двух высказываний А и В является новое высказывание С, которое истинно, если истинно хотя бы одно высказывание. Обозначение дизъюнкции: 1) С= А ∨ В (при этом говорят С равно А или В); 2) + ; 3) союз ИЛИ. .Петя сидит на западной или восточной трибуне стадиона.
Импликацией двух высказываний А (посылка) и В (заключение) является новое высказывание С, которое ложно только тогда когда посылка истинна, а заключение ложно, записывается С=А → В (при этом говорят из А следует В), очевидно что операция не симметрична Если выглянет солнце, то станет тепло
Импликация имеет следующие свойства
| A→A=1 |
| A | B | A→B | 0→A=1 |
| 0 | 0 | 1 | 1→A=A |
| 0 | 1 | 1 | A→1=1 |
| 1 | 0 | 0 | A→0=A̅ |
| 1 | 1 | 1 | A→B≠B→A |
Эквиваленцией (равнозначность) двух высказываний А и В является новое высказывание С, которое истинно только тогда, когда когда оба высказывания имеют одинаковые значения истинности, записывается 1) С=А↔В; 2) ˜, ↔,3) (тогда и только тогда). Примером может быть любое высказывание типа событие А равносильно событию В. «Две прямые параллельны тогда и только тогда, когда они не пересекаются».
Эквиваленция имеет следующие свойства
| A | B | A ↔B | |
| 0 | 0 | 1 | A↔B=B↔A |
| 0 | 1 | 0 | A↔B=B̅↔A̅ |
| 1 | 0 | 0 | A↔1=A |
| 1 | 1 | 1 | A↔0=A̅ |
Таблицу, которая показывает какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний, называют таблицей истинности.
Таблица истинности для основных логических операций
| А | В | А & В | A̅ | B̅ | A∨B | A⇒B | A⇔B |
| 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
С помощью логических перации из простых высказываний (логическ перемен и констант) можно построить логические выражения, которые будут называтся булевскими функциями например A&(B̅∨Д̅)→C . Чтобы избежать большего количества скобок в булевских функциях, принято следующее соглашение о старшинстве операций
Первыми выполняются операции в скобках, затем операции в следующем порядке: отрицание, коньюнкция, дизьюнкция, слева направо , импликация и эквиваленция.
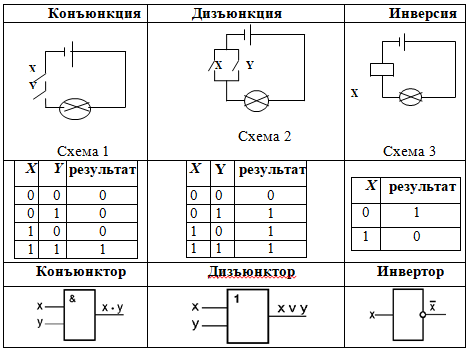
Рассмотрим еще один способ представления логических выражений - логические схемы. Существует три базовых логических элемента, которые реализуют рассмотренные нами три основные логические операции:
- логический элемент «И» логическое умножение конъюнктор;
- логический элемент «ИЛИ» логическое сложение дизъюнктор;
- логический элемент «НЕ» инверсию инвертор.
Поскольку любая логическая операция может быть пред¬ставлена в виде комбинации трех основных, любые устройства компьютера, производящие обработку или хранение информации, могут быть собраны из базовых логических элементов, как из “кирпичиков”.
Логические элементы компьютера оперируют с сигналами, представляющими собой электрические импульсы. Есть импульс логический смысл сигнала 1, нет импульса 0. На входы логического элемента поступают сигналы-значения аргументов, на выходе появляется сигнал-значение функции.
Преобразование сигнала логическим элементом задается таблицей состояний, которая фактически является таблицей истинности, соответствующей логической функции, только представлена в форме логических схем. В такой форме удобно изображать цепочки логических операций и производить их вычисления.
Конъюнктор, дизъюнктор, инвертор и условные обозначения являются стандартными и используются при составлении и описании логических схем компьютера.
Почему необходимо уметь строить логические схемы?
Дело в том, что из вентилей составляют более сложные схемы, которые позволяют выполнять арифметические операции и хранить информацию. Причем схему, выполняющую определенные функции, можно построить из различных по сочетанию и количеству вентилей. Поэтому значение формального представления логической схемы чрезвычайно велико. Логические схемы необходимо строить из минимально количества элементов, что в свою очередь, обеспечивает большую скорость работы и увеличивает надежность устройства.
Построение логических схем
Правило построения логических схем:
- определить число логических переменных;
- определить количество базовых логических операций и их порядок;
- изобразить для каждой логической операции соответствующий ей вентиль;
- соединить вентили в порядке выполнения логических операций.
Заполненная таблица:
Пример 1. Пусть Х = истина, Y = ложь. Составить логическую схему для следующего логического выражения: F = X ∨ Y & X.
Решение:
- Две переменные: Х и Y.
- Две логические операции: ∨ и &
- Строим схему:
- Ответ: 1 ∨ 0 & 1 = 0
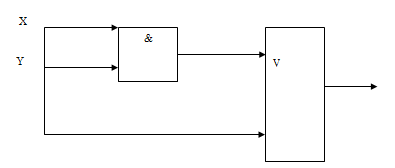
Пример 2. Постройте логическую схему, соответствующую логическому выражению: F = X & Y ∨ (Y̅∨X̅). Вычислить значения выражения для Х=1, Y=0.
Решение:
- Переменных две: Х и Y.
- Логических операций три: конъюнкция и две дизъюнкции.
- Схему строим направо в соответствии с порядком логических операций:
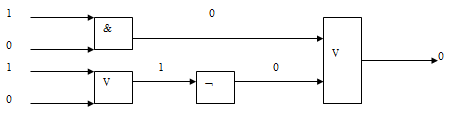
- 4. Вычислим значение выражения: F = 1 & 0 ∨ (0̅∨1̅) = 0.