1.1 Основные сведения из теории

Сосуд (резервуар) для газа или жидкости в большинстве случаев представляет собой тонкостенную осесимметричную оболочку, т. е. тело, у которого один размер (толщина) много меньше двух других размеров. Тонкостенными считают сосуды, у которых толщина стенки δ существенно (примерно более 20 раз) меньше габаритных размеров (среднего диаметра сосуда). Такие сосуды обычно используются для содержания жидкости, газа или сыпучего материала.

Формы оболочек весьма разнообразны и различаются видом срединной поверхности. Геометрическое место точек, равноотстоящих от поверхностей, ограничивающих оболочку, называют ее срединной поверхностью. Очевидно, что срединная поверхность осесимметричной оболочки представляет собой поверхность вращения – цилиндр, конус, сфера и т.д. (рисунок 1.1).

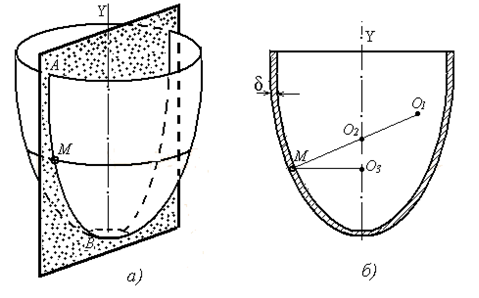
а) пересечение поверхности оболочки плоскостью; б) поперечное сечение оболочки

Рисунок 1.1 – Осесимметричная оболочка вращения

Приведем краткие сведения о геометрии поверхностей вращения. Плоскость, проходящая через произвольную точку М поверхности и ее ось симметрии (ось вращения), дает в пересечении с поверхностью кривую (в частных случаях – прямую) линию АМВ, называемую меридианом (рисунок 1.1, а). В пересечении поверхности плоскостью, нормальной к меридиану в точке М, также получается некоторая кривая (рисунок 1.2). Кривизны этой кривой и меридиана в точке М называют главными кривизнами поверхности вращения в данной точке.

Соответствующие радиусы кривизны (их также называют главными) меридиональный ρ_m (ρ_m= О₁М на рисунке 1.1, а) и окружной ρ_t (ρ_t= О₂М на рисунке 1.1, а). Радиус кривизны меридиана ρ_m может быть определен способом, известным из курса математики, если задано уравнение меридиана. Радиус кривизны ρ_t равен отрезку нормали в точке М между осью и поверхностью (отрезок ОМ на рисунке 1.2, б).

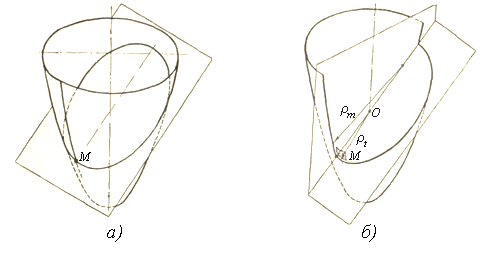
а) пересечение плоскостью, нормальной к меридиану; б) геометрические параметры точки М в плоскости сечения

Рисунок 1.2 – Пересечение поверхности оболочки

При нагружении оболочки возможны различные виды напряженного состояния. В оболочке может возникать только растяжение или сжатие без изгиба стенки (безмоментное состояние); растяжение совместно с изгибом (смешанное состояние) или только изгиб без растяжения (моментное состояние).

Примером безмоментного состояния может служить напряженное состояние, возникающее в сферической оболочке под действием равномерного внутреннего давления.

В качестве примера смешанного напряженного состояния можно указать состояние, возникающее в оболочке при нагружении ее распределенным моментом (рисунок 1.3). Под действием момента стенка оболочки изгибается, и точки, расположенные около края, получают радиальные смещения, в связи, с чем срединная поверхность оболочки растягивается в окружном направлении.

При деформации подобного вида стенка оболочки одновременно испытывает изгиб и растяжение.

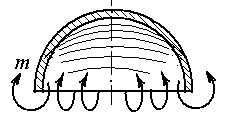
Рисунок 1.3 – Смешанное напряженное состояние

Моментное напряженное состояние может возникнуть в некоторых случаях при не симметричном нагружении оболочки. На рис. 1.4 изображен тонкостенный цилиндр со свободными торцами.

При нагружении такого цилиндра силами, перпендикулярными его оси, он будет деформироваться почти без растяжения срединной поверхности так, как показано на рисунке 1.4 штриховыми линиями.

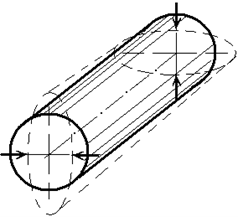
Рисунок 1.4 – Моментное напряженное состояние

Нагрузка в этом случае воспринимается исключительно за счет сопротивления изгибу. Если же изгибная жесткость будет весьма мала, то цилиндр превратится в механизм. Это следует понимать в том смысле, что его можно будет деформировать почти без затраты энергии. Так как перемещения на каждом из двух торцов могут быть заданы независимо, то такой цилиндр может быть уподоблен механизму с двумя степенями свободы. Если на один из торцов наложить связи, запрещающие искажение формы окружности, то цилиндр превратится в механизм с одной степенью свободы. При запрещении искажения формы окружности обоих торцов деформация цилиндра без растяжения срединной поверхности будет невозможна.

Преимущества оболочки как конструктивного элемента реализуются в том случае, когда ее стенка работает на растяжение (сжатие) в условиях безмоментного напряженного состояния или состояния, близкого к безмоментному.

Моментное состояние целесообразно только в том случае, когда оболочка используется в качестве гибкого элемента, получающего в процессе работы значительные упругие деформации (например, гибкое звено волновой зубчатой передачи).

Для получения безмоментного состояния в оболочке конечной толщины необходимы следующие условия:

• 1) форма оболочки должна быть плавной, не должно быть разрывного изменения радиусов кривизны;
• 2) нагрузки должны быть равномерными или плавно изменяющимися. Не должно быть сосредоточенных сил или моментов, вызывающих значительное изменение кривизны;
• 3) края оболочки должны быть закреплены таким образом, чтобы реактивные силы не имели значительной поперечной составляющей, а также, чтобы не возникали реактивные моменты;
• 4) при нагружении оболочки несимметричной нагрузкой должны быть предусмотрены связи, препятствующие возникновению чисто моментного состояния. Оболочка не должна иметь свободных открытых торцов.

Совокупность этих четырёх условий позволяет принять напряжение неизменным по толщине стенки и, следовательно, стенки сосуда работают только на растяжение (сжатие).

При нарушении любого из четырёх условий, допущение о равномерности напряжении по толщине стенки отпадает.

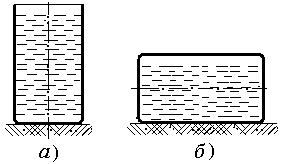
а) симметричное нагружение; б) не симметричное нагружение

Рисунок 1.5 – Варианты нагружения оболочки

Цистерна с нефтью в положении а) на рисунке 1.5 может быть рассчитана по безмоментной теории, но если цистерну положить на бок (рисунок 1.5, б), то напряжения в стенках будут подчиняться более сложному закону.

Очевидно, что условие тоностенности ограничивает область применения безмоментной теории сосудами, испытывающими весьма малые нагрузки. Практически в резервуарах и газгольдерах, рассчитываемых по этой теории, давление на стенки не должно выходить за пределы 2÷2,5 атмосфер (кг/см²). 1атм = 10⁵ Н/м² = 0,1 МН/м².

Следует заметить, что даже если эти условия не полностью соблюдаются и в оболочке возникает растяжение и изгиб, безмоментная теория не теряет своего значения, так как уже на небольшом расстоянии от зоны изгиба (от места приложения сосредоточенных сил или скачкообразного изменения радиусов кривизны) напряженное состояние обычно можно рассматривать как безмоментное.

На краях оболочки, где приложены распределенные поперечные силы или моменты, напряженное состояние можно рассматривать как местный изгиб стенки оболочки около края.

Для расчета на прочность тонкостенных сосудов (точнее говоря, для определения напряжений, возникающих в их стенках), находящихся под действием внутреннего осесимметрично распределенного давления р газа или жидкости, выделяют бесконечно малый элемент оболочки двумя бесконечно близкими меридиональными сечениями и двумя плоскостями, нормальными к меридиану (рисунок 1.6). Отдельно этот элемент показан на рисунке 1.7, а. На его гранях возникают только нормальные напряжения, т. е. эти грани для точки М главные площадки.

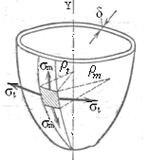
Рисунок 1.6 – Геометрические параметры и напряжённое состояние бесконечно малого элемента оболочки

Напряжение σ_t в меридиональном сечении называют окружным (или кольцевым), а напряжение σ_m в сечении, перпендикулярном к меридиану, – меридиональным напряжением.

Для тонкостенного сосуда (оболочки) принимают, что эти напряжения равномерно распределены по толщине δ стенки оболочки. Из уравнения равновесия элемента (условия равенства нулю проекций всех сил на нормаль к поверхности элемента) вытекает зависимость, называемая уравнением Лапласа

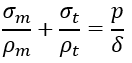
Отметим, что вблизи внутренней поверхности оболочки кроме напряжений σ_t и σ_m возникают также радиальные нормальные напряжения σ_r, равные по модулю давлению p (на рисунке 1.7, б показан бесконечно тонкий элемент, выделенный вблизи внутренней поверхности оболочки, а на рисунке 1.7, в – вблизи внешней). Однако, как следует из уравнения Лапласа, напряжения σ_m и σ_t имеют порядок 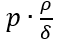(ρ – характерный радиус кривизны), т.е. во много раз превышают σ_r, так как ρ/δ≫1 (рассматриваются тонкие оболочки).

Следовательно, величиной σ_r можно пренебречь и считать напряженное состояние во всех точках стенки оболочки плоским.

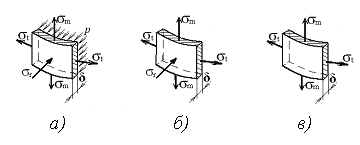
а) под действием внутреннего давления; б) вблизи внутренней поверхности; в) вблизи внешней поверхности

Рисунок 1.7 – Напряжённое состояние элемента оболочки

В частных случаях при ρ_m=∞ (цилиндрические или конические оболочки) из уравнения Лапласа непосредственно определяется величина σ_t. В общем случае, вначале определяют величину σ_m. Для этого рассекают оболочку коническим сечением, нормальным к срединной поверхности, и составляют уравнение равновесия для оставленной части – условие равенства нулю проекций на ось вращения всех сил, приложенных к отсеченной части (рисунок 1.8). Подчеркнем, что нормальное коническое сечение можно представить как бесчисленное множество сечений плоскостями, нормальными к меридианам во всех точках окружности.

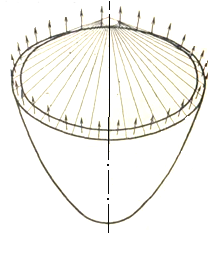
Рисунок 1.8 – Коническое сечение

При составлении указанного уравнения равновесия целесообразно пользоваться приемом, который часто называют «принципом отвердения». Состоит он в том, что, рассекая оболочку нормальным коническим сечением, одновременно «рассекают» и газ (или жидкость), находящийся в ней под давлением. Отбрасывая одну часть оболочки, одновременно отбрасывают и газ, а действие отброшенного газа (или жидкости, или того и другого) на оставшийся заменяют соответствующим давлением

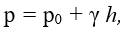
где p₀ – давление газа над поверхностью жидкости;

γ – удельный вес жидкости;

h – глубина – расстояние от свободной поверхности жидкости до сечения (рисунок 1.9, а).

Отметим, что равнодействующую сил давления проще определять, если рассекать жидкость или газ плоскостью, нормальной к оси вращения оболочки, что не мешает рассекать оболочку коническим сечением, нормальным к меридиану, как показано на рисунок 1.9, б.

Изложенная теория определения напряжений (так называемая безмоментная теория оболочек) для тонкостенных осесимметричных оболочек при отсутствии нагрузок в виде сосредоточенных сил и моментов, непрерывном изменении радиуса кривизны меридиана ρ_m и толщины стенки δ и при отсутствии изломов меридиана обеспечивает точность, вполне достаточную для инженерных расчетов.

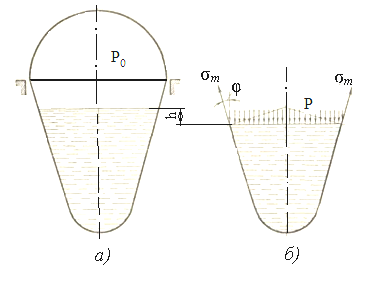
а) положение произвольного сечения; б) расчётная схема для уравнения равновесия

Рисунок 1.9 – Оболочка под действием жидкости или газа

Напряжения изгиба, возникающие в стенках оболочек в местах жестких закреплений и в местах скачкообразного изменения кривизны меридионального сечения, носят местный характер и быстро затухают по мере удаления от зон их возникновения.

Заметим, что при инженерных расчетах обычно не учитывают различий в величинах радиусов кривизны внутренней, срединной и наружной поверхностей оболочки.

Для определения опасной точки (точек) сосуда во многих случаях целесообразно построение эпюр σ_t и σ_m. Когда опасная точка установлена, по известным для нее главным напряжениям σ_m и σ_t находят по выбранной гипотезе прочности эквивалентное напряжение и составляют условие прочности, как показано в приведенных ниже примерах.

Сферические сосуды. Расположение главных площадок и направления главных напряжений показаны на рисунке 10, а).

Уравнение Лапласа для сферической оболочки (ρ_m=ρ_t=R) будет иметь вид

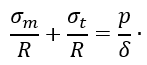
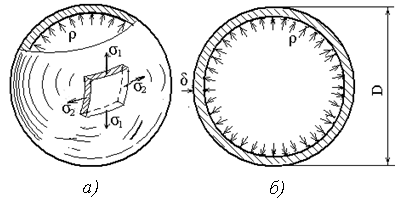
а) напряжённое состояние элемента; б) поперечное сечение оболочки

Рисунок 1.10 – Сферическая оболочка

В сферическом сосуде ,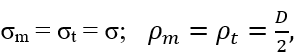

подставив в уравнение Лапласа,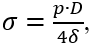

поэтому главные напряжения σ₁ и σ₂ принимают равные значения

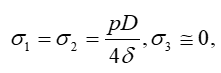
где p – давление газа или жидкости, н/м² (amм);

D – диаметр сосуда, м (см);

δ – толщина стенки, м (см).

Условие прочности, согласно теории наибольших касательных напряжений (ІІІ теории прочности), в силу того, что σ₃ = 0, запишется в виде

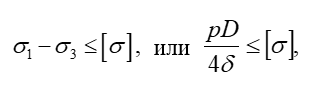
откуда необходимая толщина стенки

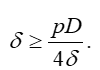
Условие прочности, согласно теории энергии формоизменения (пятой теории прочности), при σ₃=0 имеет вид

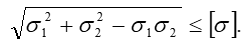
Подставляя значения главных напряжений, получим

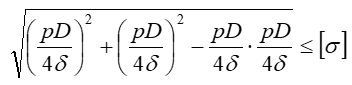
или

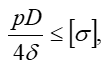
откуда

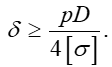
Следовательно, при проектном расчете тонкостенных сферических сосудов по ІІІ и V теориям прочности получаем одну и ту же расчетную формулу толщены стенки.

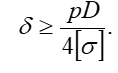
Цилиндрические сосуды. Расположение главных площадок и направления главных напряжений показаны на рисунке 1.11

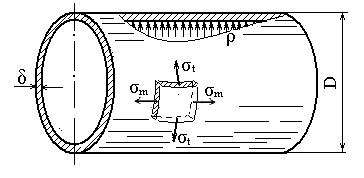
Рисунок 1.11 – Напряжённое состояние цилиндрического сосуда.

Для цилиндрической оболочки

Подставив эти значения в уравнение Лапласа

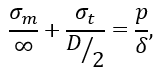
следовательно

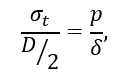
откуда

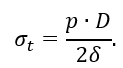
Условие равновесия одной из частей цилиндра под воздействием внешних сил p и внутренних усилий имеет вид

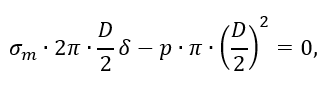
откуда

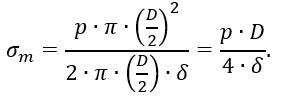
В этом случае

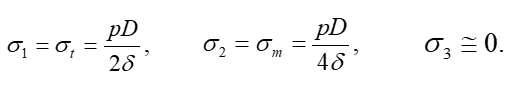
Реализуя условие прочности, согласно ІІІ теории прочности, приходим к неравенству

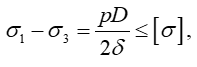
откуда толщина стенки

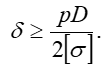
Проделывая то же самое с использованием V теории прочности, получим

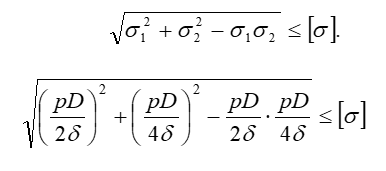
или

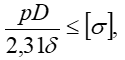
откуда

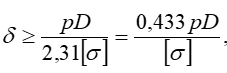
следовательно, толщина стенки при расчете цилиндрического тонкостенного сосуда по V теории прочности получается на 13,5 % меньше, чем при расчете по ІІІ теории прочности.

При наличии окисляющей среды расчетную толщину стенки следует увеличить на 1-3 _mm для компенсации возможного ослабления в результате коррозии.

Конические сосуды. Отсечем часть конической оболочки нормальным коническим сечением с углом 2φ при вершине и рассмотрим равновесие отсеченной части.

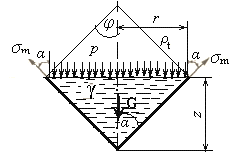
Рисунок 1.12 – Расчётная схема конической оболочки

Как видно из рисунка 1.12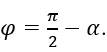

Уравнение равновесия отсеченной части оболочки будет иметь вид

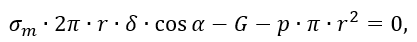
где 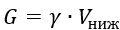– вес жидкости, заполняющий отсеченную часть конуса.

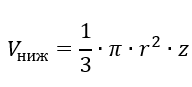
С учетом V_ниж, уравнение равновесия имеет следующий вид

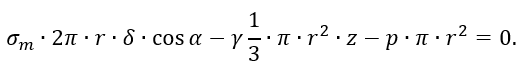
Из этого уравнения можно рассчитать величину меридионального напряжения σ_m и, подставив его в уравнение Лапласа, найти величину σ_t.

Возможно отделение сечением не нижней, а верхней части оболочки с последующей записью уравнения равновесия. Это делается для того, чтобы при составлении условий равновесия отсеченного элемента крепление оболочки не попадало в схему отсеченной части. В подобных вариантах во всех рассмотренных случаях изменится знак силы G, т.к. в этом случае ее направление будет совпадать с направлением вертикальной составляющей напряжения σ_m.

В этом случае, при расчете величины G, в качестве объема будет браться объем отсеченной верхней части V_верх, а при расчете величины p в формулу p=h_верх·γ во всех случаях войдет величина h_ниж – высота столба жидкости в отсеченной нижней части оболочки. В остальном порядок расчета останется неизменным.

В случае, если жидкость находится в сосуде под давлением р, то при расчете величины p добавляется величина давления р. Формула давления будет иметь следующий вид

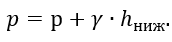
В некоторых задачах отсеченная часть представляет собой не какой-то один элемент, а два или более состыкованных элемента. При этом вид уравнений равновесия остается неизменным, а изменяется только величина объема верхней или нижней части сосуда.