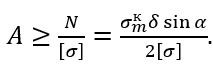Тонкостенными считают сосуды, у которых толщина стенки δ существенно (примерно более 20 раз) меньше габаритных размеров (среднего диаметра сосуда).

Такие сосуды (рисунок 2.1, а) обычно используются для содержания жидкости, газа или сыпучего материала. В этих случаях нагрузкой является внутреннее давление содержимого материала на стенки сосуда, направленное перпендикулярно к стенке и распределенное, как правило, симметрично относительно оси вращения у. Такую нагрузку называют осесимметричной. Если стенки сосуда не имеют резких изломов и переходов, а нагрузкой является, в основном, внутреннее давление нормальное к стенке, то допускают, что стенки сосуда будут испытывать двухстороннее растяжение с равномерным законом распределения напряжений по толщине стенки. Изгиба стенок не будет, а поэтому расчет можно производить по безмоментной теории.

а) геометрические параметры и напряжённое состояние произвольной точки М; б) расчётная схема произвольного сечения

Рисунок 2.1 – Тонкостенный сосуд

По безмоментной теории, из условия равновесия элемента, выделенного около рассматриваемой точки М (рисунок 2.1, а) бесконечно близкими меридиональными и перпендикулярными им (коническими) сечениями, получается одно уравнение – уравнение Лапласа, для определения окружных σ_t и меридиональных σ_m напряжений:

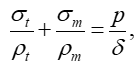
где ρ_t и ρ_m – радиусы кривизны окружного и меридионального сечений сосуда на уровне рассматриваемой точки М;

p – интенсивность давления на этом уровне, являющаяся функцией только координаты у;

δ – толщина стенки сосуда.

В уравнении Лапласа два неизвестных σ_t и σ_m, и, как правило, одного этого уравнения оказывается недостаточно для определения этих напряжений.

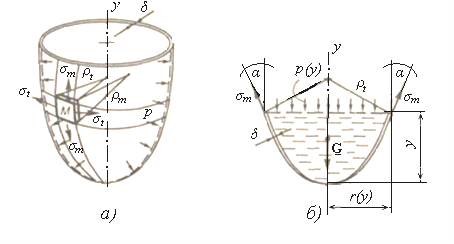
Второе уравнение составляется как условие равновесия части сосуда, отделенной коническим сечением, перпендикулярным меридианам на уровне рассматриваемой точки (рисунок 2.1, б).

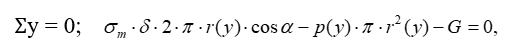
откуда

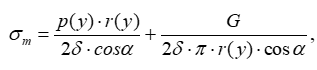
где p(y) – внутреннее давление в сосуде на уровне y;

r(y) – радиус окружности кольцевого сечения на том же уровне;

α – угол между осью y и касательной к меридиану;

G – вес содержимого в отсеченной части сосуда.

Обычно собственный вес тонкостенного сосуда не учитывают.

Решая совместно уравнения (2.1) и (2.2) можно определить напряжения σ_t и σ_m. Следовательно, по безмоментной теории напряжения, возникающие в стенке сосуда, определяются из уравнений равновесия, т.е. задача является статически определимой. При составлении уравнений равновесия следует иметь в виду во-первых, что при действии на поверхность произвольной формы давления p, нормального к этой поверхности с равномерной интенсивностью, величина равнодействующей такого давления равна произведению давления p на площадь A_np, представляющую собой проекцию поверхности A на плоскость, перпендикулярную заданной оси y (рисунок 2.2), т.е. P_y = p A_np.

Во-вторых, независимо от формы сосуда вертикальная составляющая силы давления жидкости на какую-либо поверхность равна весу жидкости в объеме, расположенном над поверхностью.

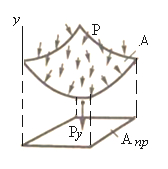
Рисунок 2.2 – Схема замены произвольных распределённых сил p равнодействующей силой P_y

Так как напряженное состояние в рассматриваемой точке М (рисунок 2.1, а) является сложным, то расчет на прочность производится по известным гипотезам прочности.

На внутренней поверхности стенки сосуда действует третье главное напряжение σ_r = -p(y). В большинстве случаев оно мало по сравнению с σ_t и σ_m и при расчете на прочность им можно пренебречь, поэтому напряженное состояние можно считать плоским. Безмоментная теория расчёта тонкостенных сосудов (оболочек) является вполне удовлетворительной, если граничные условия являются безмоментными, т.е. обеспечивают краям сосуда свободные перемещения в направлении нормали к поверхности. Если край сосуда закреплен от смещения по нормали к поверхности, то в закреплении возникают реакции, вызывающие изгиб, который быстро затухает при удалении от края. Быстро затухающее напряженное состояние, возникающее в результате искривления срединной поверхности тонкостенных оболочек, называют краевым эффектом.

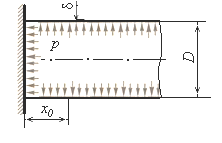
Рисунок 2.3 – Цилиндрическая оболочка с жёстко защемленным концом_y

Например, краевой эффект возникает при наличии жестко защемленного края цилиндрической оболочки, находящейся под действием внутреннего давления (рисунок 2.3). Зона распространения краевого эффекта в этом случае по длине оболочки составляет 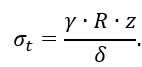Это обычно величина малая по сравнению с общей длиной оболочки. Однако в этой зоне безмоментная теория расчета становится неприменимой. Краевой эффект может привести к заметному повышению максимальных напряжений. Аналогичный всплеск напряжений возникает и по месту стыка цилиндрической оболочки с полусферической или конической оболочками. Если представить себе, что цилиндрическая оболочка и полусферическое днище деформируются независимо друг от друга (рисунок 2.4), то по безмоментной теории для цилиндрической оболочки:

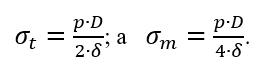
Относительная деформация в окружном направлении:

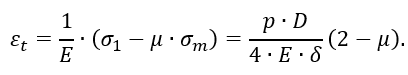
Перемещение в радиальном направлении:

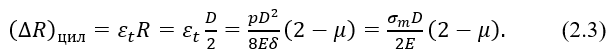
Для сферической оболочки по безмоментной теории:

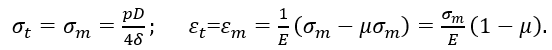
Перемещение в радиальном направлении:

Сравнивая радиальные перемещения (2.3) и (2.4) срединной поверхности видим, что перемещения в цилиндрической оболочке больше, чем в сферической ((∆R)_цил > (∆R)_сф).

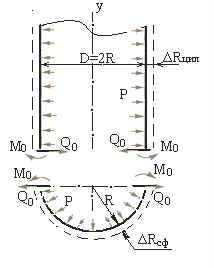
Рисунок 2.4 –Схема нагрузок, внутренних усилий и деформаций на стыке цилиндрической и сферической частей сосуда

В действительности цилиндр и днище составляют целое и должны работать совместно.

Вследствие этого по месту стыка происходит нарушение плавной сопряженности срединных поверхностей и наряду с безмоментными напряжениями возникают дополнительные напряжения от погонных силовых факторов M_o – изгибающего момента и Q_Q – поперечной силы.

Эти дополнительные напряжения носят явно выраженный местный характер. Если материал оболочки пластичный, то повышение напряжений из-за краевого эффекта при статическом нагружении может привести, лишь к местным пластическим деформациям и не скажется существенным образом на несущей способности оболочки в целом. Для уменьшения влияния краевого эффекта в местах возможного его появления обычно делают дополнительные подкрепления в виде упорного кольца (рисунок 2.5, а) или создают местные утолщения оболочки, загибая края днища внутрь оболочки (рисунок 2.5, б).

Например, по месту излома сосуда на стыке цилиндрической и конической частей (см. рисунок 2.5, а) от меридионального напряжения σ_m^к, конической части возникает σ₀ на радиальное направление. Поэтому здесь устанавливают упорное кольцо, воспринимающее этот распор сосуда.

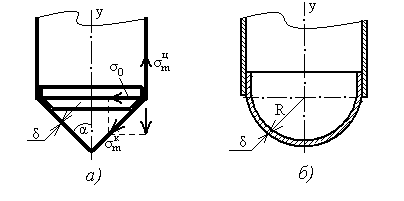
а) напряжения в стыке; б) поперечное сечение на стыке двух частей сосуда

Рисунок 2.5 – Схема соединения стыка

Распределенная распорная нагрузка на кольцо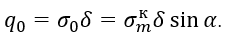

Сжимающая нормальная сила в поперечном сечении кольца

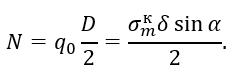
По условию прочности кольца

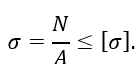
Отсюда необходимая площадь поперечного сечения распорного кольца