Пример 1. Построить эпюры меридиональных и окружных напряжений для тонкостенного резервуара, в котором находится газ под давлением р₀= 20 кГ/см²(рисунок 1.13). Толщина стенки сосуда δ = 5 _mm; диаметр срединной поверхности цилиндрической оболочки D= 2R= 500 _mm. Резервуар считать невесомым.

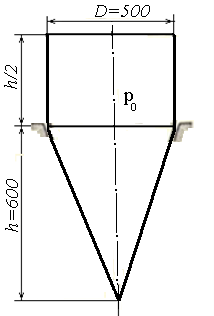
Рисунок 1.13 – Геометрические параметры комбинированного сосуда

Решение. Задача, естественно, распадается на две:

1) определение напряжений σ_m и σ_t в цилиндрической части резервуара;

2) то же в конической части.

Рассечем цилиндрическую часть резервуара плоскостью, нормальной к его оси, отбросим нижнюю часть и заменим действие отброшенной части на оставленную соответствующими усилиями (рисунок 1.14). Это будут, во-первых, силы, соответствующие напряжениям, σ_m равномерно распределенным по сечению стенки резервуара, и, во-вторых, силы, обусловленные давлением газа р₀, которое согласно «принципу отвердения» можно приложить непосредственно к газу, находящемуся в верхней части резервуара. Эти силы нормальны к секущей плоскости.

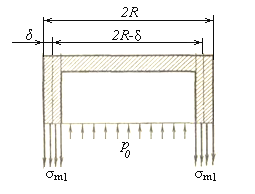
Рисунок 1.14 – Расчётная схема верхней части сосуда

Составим уравнение равновесия для оставленной части сосуда (условие равенства нулю суммы проекций всех сил на вертикальную ось)

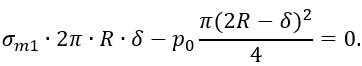
Здесь первый член – равнодействующая системы сил, обусловленных возникновением меридиональных напряжений (2πRδ – площадь кольца, образованного сечением стенки резервуара).

Второй член – равнодействующая сил давления газа. Площадь круга, по которой распределено давление р₀, вычислена по размерам, указанным на рисунке. 1.14. Однако, учитывая, что 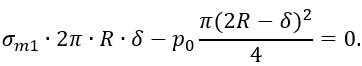величиной δ по сравнению с 2R можно пренебречь и тогда уравнение равновесия примет вид

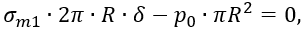
откуда

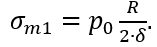
Подставляя числовые данные, получаем

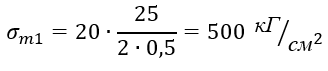
Окружные напряжения σt определим из уравнения Лапласа

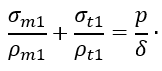
В рассматриваемой задаче ρ_m1=∞; ρ_m1=R и ρ = ρ₀ и уравнение Лапласа упрощается

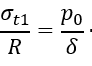
отсюда

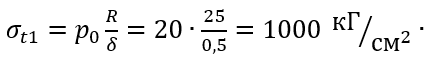
Заметим, что, в рассматриваемом случае можно сначала определить𝜎_t1, а не 𝜎_m1, так как в уравнение Лапласа величина 𝜎_m1 не вошла.

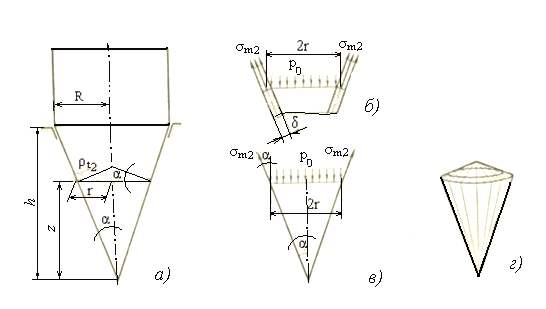
а) параметры конического сечения; б) расчётная схема верхней части конуса; в) расчётная схема нижней части конуса; г) поверхность усечённого конуса

Рисунок 1.15 – Расчётные схемы нижней части сосуда

Для конической части резервуара принципиально задача решается аналогично.

Для определения σ_m стенку резервуара (рисунок 1.15, а) необходимо разрезать нормальным коническим сечением; газ же удобнее «резать» горизонтальной плоскостью (рисунок 1.15, б, в), так как при этом выражение для равнодействующей сил давления упрощается.

На основе рисунка 1.15, б составим уравнение равновесия сил, действующих на нижнюю оставленную часть сосуда

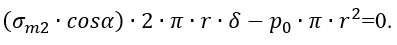
Здесь σ_m2 cosa – вертикальная составляющая меридионального напряжения. При определении площади, по которой действует давление р_m, учтено, что δ∙≪∙r, т. е. принято(2r-δ)²≈(2r)². Поверхность усеченного конуса, на которой возникают напряжения σ_m2 (ее площадь принята равной 2πrδ), показана отдельно на рисунке 1.15, г.

Из составленного уравнения равновесия имеем

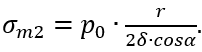
Подставляя сюда 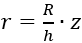что следует из рисунка 1.15, а, получаем окончательно

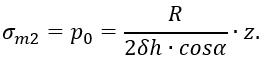
Определим σ_t2. Очевидно, что в данном случае p_m=∞ и из уравнения Лапласа следует/p>

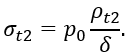
Учитывая, что р = р₀ и

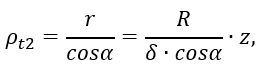
получаем окончательно

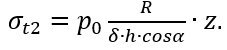
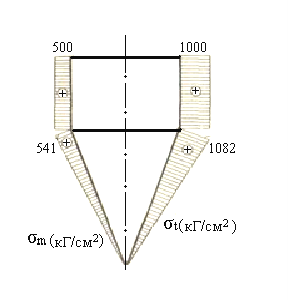
Рисунок 1.16 – Эпюры напряжений в стенках резервуара

Эпюры напряжений σ_t и σ_m , построенные по полученным выражениям при заданных значениях величин р₀, R, h, σ, показаны на рисунке 1.16.

Выясним происхождение скачков напряжений при переходе от цилиндрической части резервуара к конической. Скачок в величине σ_m как следует из сравнения выражений (1.1) и (1.3) (при z = h), появляется за счет cos α в знаменателе выражения (1.3). Механический смысл этого обстоятельства становится ясным, если рассмотреть равновесие бесконечно тонкого пояса, вырезанного на границе стыка двух оболочек, т. е. цилиндрической и конической частей сосуда (рисунок 1.17).

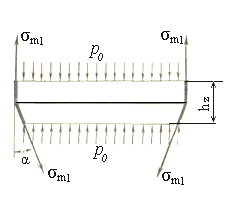
Рисунок 1.17 – Расчётная схема пояса, вырезанного на границе стыка

Поскольку реакция опоры отсутствует (резервуар считается невесомым) и давления р₀ сверху и снизу взаимно уравновешиваются, то равновесие возможно лишь при условии (σ_m2∙cosα) = σ_m1. Разумеется, этот вывод верен лишь в том случае, если толщины обеих оболочек одинаковы.

Скачок в величине σ_t определяется скачком в величине p₀ в уравнении Лапласа, которое для обеих оболочек принимает вид

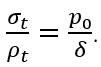
Для того чтобы разобраться в сути вопроса, необходимо вспомнить, как получено уравнение Лапласа. А именно, это уравнение следует из условия равенства нулю суммы проекций всех сил, приложенных к бесконечно малому элементу стенки оболочки, на нормаль к срединной поверхности.

Вырезая такие элементы для каждой из оболочек (рисунок 1.18, а) и глядя на каждый из них вдоль образующей (рисунок 1.18, б), убеждаемся, что из условия ρ_t1 >ρ _t2 при равных дугах ds следует dφ₂ < dφ₁. А поскольку в обоих случаях напряжения σ_t2 и σ_t1 должны уравновесить одну и ту же по величине равнодействующую силу давления p₀,то из условия dφ₂ < dφ₁ следует σ_t2 >σ _t1. Если произвести вычисления, то получим

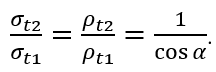
В заключение сделаем одно замечание общего характера. При составлении уравнений равновесия мы умышленно допускали погрешность, имеющую порядок δ/R (пренебрегали величиной δ по сравнению с радиусом срединной поверхности). Дело здесь не только в том, что погрешность эта, мала. Здесь действует гораздо более принципиальное соображение: при решении задач теории оболочек бессмысленно вносить уточнения, имеющие порядок δ/R, поскольку сами соотношения теории оболочек имеют погрешность того же порядка.

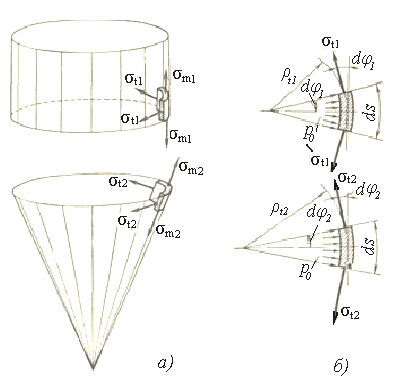
а) в пространстве; б) вдоль образующей

Рисунок 1.18 – напряжения σ_t и σ_m, действующие на стыке сосуда

Пример 2. Проверить прочность газгольдера (рисунок 1.19): - материал газгольдера – низколегированная сталь с пределом текучести σ_т = 360 МПа,

- давление газа – р₀ = 15 бар.,

- требуемый коэффициент запаса прочности – [n_т] = 1,8.

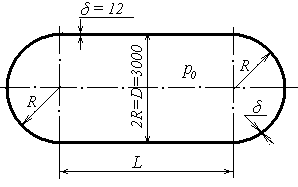
Рисунок 1.19 – Параметры газгольдера

Решение. Как было установлено, в точках стенок резервуаров возникает плоское напряженное состояние, и, следовательно, условие прочности имеет вид

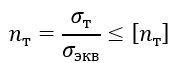
где n_т – действительный коэффициент запаса прочности по текучести;

σ_экв – эквивалентное напряжение в опасной точке сосуда.

Для определения эквивалентного напряжения в опасной точке сосуда требуется предварительно найти главные напряжения (окружное и меридиональное напряжения) в этой точке.

Применяя метод сечений для цилиндрической части газгольдера (рисунок 1.20, а) и составляя уравнение равновесия

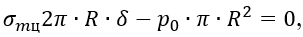
получаем

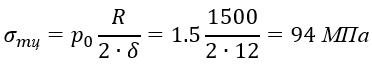
Напомним, что 1 бар = 0,1 _н/мм² = 0,1МН/_м²/p>

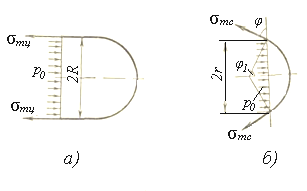
а) цилиндрическая часть; б) сферическая часть

Рисунок 1.20 – Расчётная схема газгольдера

Полагая в уравнении Лапласа ρ_m=∞, ρ₀=R и p=p₀, найдем окружное напряжение σ_tц для цилиндрической части газгольдера

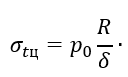
Проделаем то же самое для сферической части. Производя разрез нормальным коническим сечением, отбрасывая левую часть и заменяя ее действие на правую напряжениями σ_mc и давлением р₀ (рисунок 1.2, б), получаем возможность определить σ_mc в сферической части из уравнения равновесия

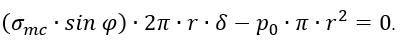
Или

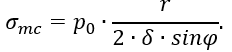
Учитывая, что r = Rsin φ, окончательно получаем

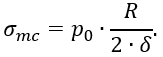
Уравнение Лапласа для сферической оболочки (ρ_m=ρ_t=R) будет иметь вид

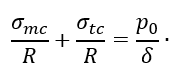
Отсюда

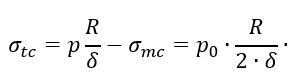
Отметим, что ту же задачу можно было решить значительно проще. Действительно, из симметрии сферической оболочки и симметрии нагружения следует, что σ_mc=σ_tc. Тогда, положив в уравнении Лапласа σ_mc=σ_tc, получим

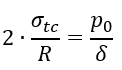
или

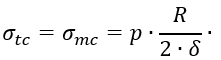
Эпюры напряжений σ_m и σ_t показаны на рисунке 1.21,а.

Очевидно, опасным является цилиндрический участок газгольдера. Элемент, вырезанный в произвольной точке цилиндрического участка, изображен на рисунке 1.21,б. Строго говоря, здесь следовало бы показать и напряжение σ_r в направлении нормали к срединной поверхности. Однако это напряжение, как уже указывалось, мало по сравнению с σ_m и σ_t (наибольшего значения оно достигает у внутренней поверхности, где σ_r = - p = - 1,5 Н/_mm²= -1,5 МПа) и им можно пренебречь.

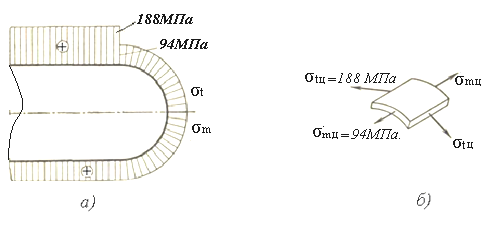
а) эпюры σ_t и σ_m; б) напряжения σ_t и σ_m на бесконечно малом элементе цилиндрического участка оболочки

Рисунок 1.21 – Механические напряжения в газгольдере

Вычислим эквивалентное напряжение для любой из опасных точек, применив гипотезу прочности энергии формоизменения (IV гипотеза прочности).

Поскольку σ_tц σ_mц, то

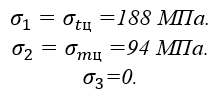
По четвёртой теории прочности имеем

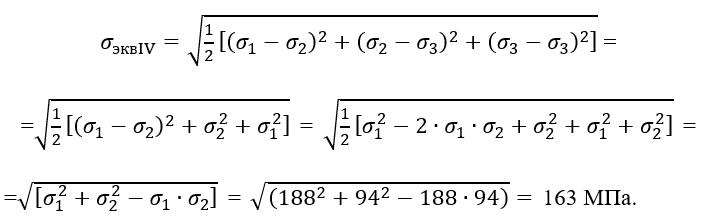
Коэффициент запаса прочности по отношению к пределу текучести

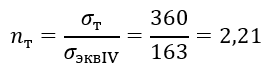
что примерно на 23% выше требуемого.

В заключение объясним скачок σ_t при переходе от цилиндрического участка к сферическому. Происхождение этого скачка становится ясным после сравнения элементов, вырезанных из стенок цилиндрического и сферического участков (рисунок 1.22). Действительно, для первого элемента (рисунок 1.22, а) равнодействующая dP сил давления уравновешивается только напряжениями σ_tц (меридиональные напряжения не дают проекции на нормаль к элементу). Что касается второго элемента (рисунок 1.22, б), то здесь σ_tс и σ_mc дают равные проекции на нормаль, вследствие чего каждое из них оказывается в два раза меньше, чем σ_tц.

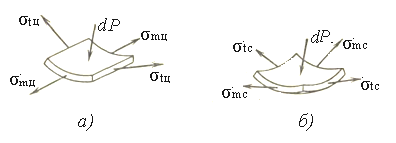
а) цилиндрический участок; б) сферический участок

Рисунок 1.22 – Напряжения, действующие на бесконечно малом элементе

Пример 3Сравнить прочность двух заполненных жидкостью резервуаров, отличающихся только условиями закрепления (рисунок 1.18). Применить гипотезу наибольших касательных напряжений.

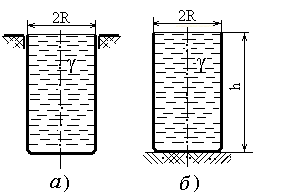
а) опора сверху; б) опора снизу

Рисунок 1.23 – резервуары с жидкостью

Решение. Задача сводится к сравнению величин эквивалентных напряжений для опасных точек обоих резервуаров. Опасная точка каждого из резервуаров определяется в результате анализа эпюр, показывающих изменение величины эквивалентных напряжений по высоте стенки резервуара, если h, R, δ, γ заданы.

Для той же цели можно ограничиться построением и анализом эпюры главных напряжений, так как по ним легко сопоставить величины эквивалентных напряжений для различных точек стенок.

Уравнение равновесия для первого случая (рисунок 1.24, а) имеет вид

σ_m∙2πR∙δ-p∙π∙R²-G=0

где р = γ z – гидростатическое давление жидкости на уровне z;

γ – удельный вес жидкости;

G= γ·π·R²·(h—z) – вес жидкости в оставленной (верхней) части резервуара.

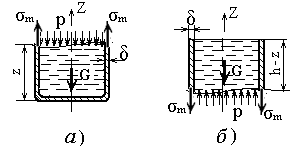
а) для опоры сверху; б) для опоры снизу

Рисунок 1.24 – Расчётные схемы резервуаров с жидкостью

Подставив в уравнение равновесия значения р и G, получим

σ_m∙2πR∙δ-γ∙z∙π∙R²-γ∙π∙R² (h-z)=0

откуда окончательно

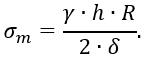
Составляя уравнение равновесия для второго случая (рисунок 1.24,б), имеем

σ_m∙2πR∙δ-p∙π∙R²+G=0

или после подстановки выражений для р и G

σ_m∙2πR∙δ-γ∙z∙π∙R²+γ∙π∙R²∙z=0

откуда

σ_m=0

Столь различные результаты не должны вызывать недоумения. Действительно, и в том и в другом варианте вес всей жидкости воспринимается днищем резервуара. Но во втором случае он непосредственно передается на опору, в то время как в первом случае передача этого усилия на опору осуществляется через стенку резервуара.

Определим окружные напряжения. Очевидно, они в обоих резервуарах будут одинаковы, поскольку закон распределения гидростатического давления не зависит от условий закрепления.

Уравнение Лапласа для цилиндра в обоих случаях имеет вид

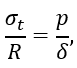
так - как в уравнении Лапласа ρ_t=R, ρ_m=∞, откуда, полагая p = γ∙z, имеем

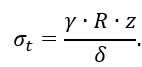
Эпюры σ_m и σ_t, построенные по полученным зависимостям, показаны на рисунке 1.25. Как следует из этих эпюр, в стенке первого резервуара (рисунок 1.25,а) всюду (за исключением верхней кромки) имеет место плоское напряженное состояние. При этом в верхней части (при z>h/2) σ_m>σ_t, следовательно, σ₁=σ_m и σ₂=σ_t, (σ₃=0). В нижней же части σ_t>σ_m и здесь σ₁=σ_t , а σ₂=σ_m. Таким образом, эпюра σ₁ в верхней части будет совпадать с эпюрой σ_m, а в нижней – с эпюрой σ_t, а эпюра σ₂ – наоборот (рисунок 1.26).

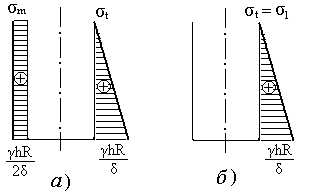
а) для первого резервуара; б) для второго резервуара

Рисунок 1.25 – Эпюры σ_m и σ_t

Для второго случая (рисунок 1.25, б) в любой точке стенки возникает линейное напряженное состояние (σ_m=0, σ₁=σ_t, σ₂=σ₃=0) и эпюра σ_t одновременно является эпюрой σ₁.

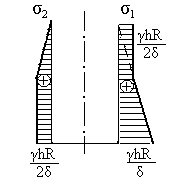
Рисунок 1.26 – Эпюра главных напряжений в стенках первого резервуара

Переходим к окончательному этапу решения задачи – сравнению прочности резервуаров. Опасными в обоих случаях являются точки, лежащие в непосредственной близости к днищам, где наибольших (и равных) значений достигают главные напряжения σ₁. Поскольку в выражение для эквивалентного напряжения по третьей теории прочности (гипотезе прочности максимальных касательных напряжений) σ₂ не входит, то и в первом и во втором резервуарах

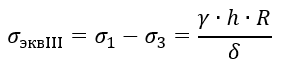
и, следовательно, резервуары равнопрочные.

Для сравнения – по четвёртой теории прочности (гипотезе прочности энергии формоизменения): В первом резервуаре

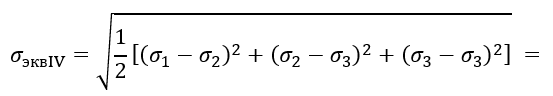
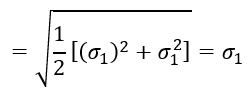
Во втором резервуаре

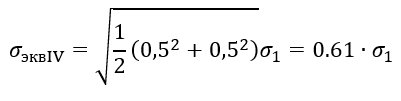
Пример 4. Из условия прочности определить, до какого уровня Н можно заполнить жидкостью с удельным весом γ = 14·10³ Н/_m³ конический резервуар (рисунок 1.27) при толщине стенки δ = 6 мм, высоте Н₀= 9 м и радиусе основания R₀= 4,5м. Принять [σ] = 50 Н/_мм². Применить гипотезу наибольших касательных напряжений.

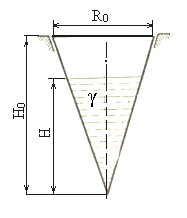
Рисунок 1.27 – Параметры резервуара.

Решение. Искомая величина Н может быть определена из условия прочности, если предварительно эквивалентное напряжение для опасной точки будет выражено через Н.

Положим Н < H₀. Тогда при построении эпюр напряжений σ_m и σ_t будем иметь два участка. Проводя сечение на первом (верхнем) участке (рисунок 1.28, а) и составляя уравнение равновесия, получаем

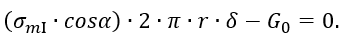
Здесь 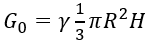– вес всей жидкости, залитой в резервуар.

Из уравнения равновесия с учетом значения G₀ найдем

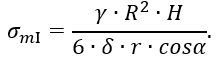
Учитывая, что r=z∙tgα и R=H∙tgα (рисунок 1.28, а), получаем окончательно

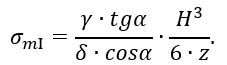
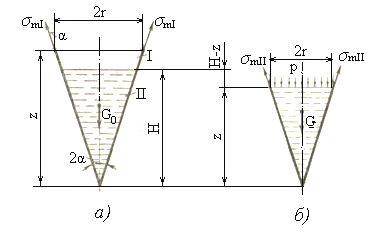
а) I – участок выше уровня жидкости; б) II – участок ниже уровня жидкости

Рисунок 1.28 –

Поскольку на участке I давление на стенку отсутствует, то из уравнения Лапласа следует, что σ_tI=0.

Перейдем к участку II (нижнему). При составлении уравнения равновесия для нижней отсеченной части здесь кроме веса жидкости 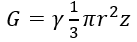следует учесть равнодействующую сил гидростатического давления, равную γ(H-z)πr² (рисунок 1.28, б).

Уравнение равновесия будет иметь вид

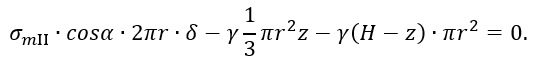
Отсюда

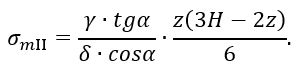
Выражение для σ_tII получим, как обычно, из уравнения Лапласа, положив в нем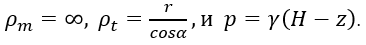

Таким образом,

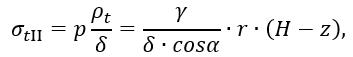
или после подстановки r=z∙tgα

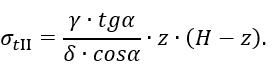
Итак, получены следующие выраженияпри z ≥ H

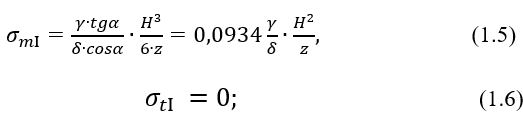
при z ≤ H

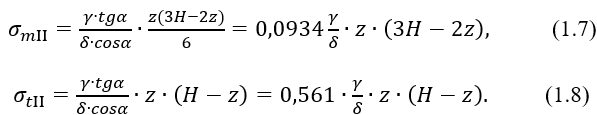
Здесь учтено, что

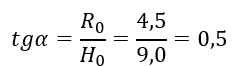
и

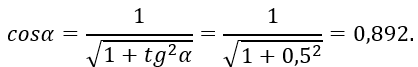
Для построения эпюр необходимо определить точки экстремумов функций σ_m (z) и σ_t (z) на втором участке.

Продифференцировав выражения (1.7) и (1.8), найдем, что

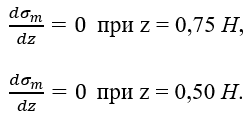
Подставив эти значения z в выражения (1.7) и (1.8), получим максимальные значения напряжений max σ_mII и max σ_tII:

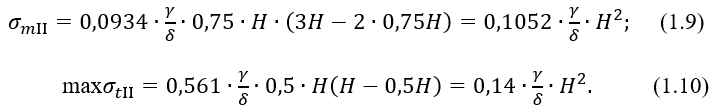
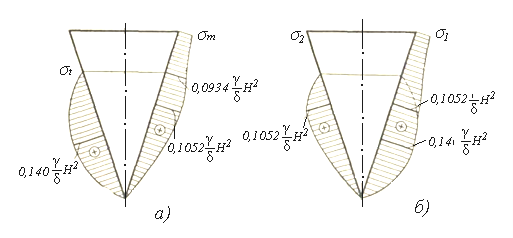
а) эпюры σ_m и σ_t; б) эпюры главных напряжений

Рисунок 1.29 – Эпюры напряжений в стенках резервуара

Эпюры σ_m и σ_t, (построенные по выражениям (1.5) – (1.10) для произвольного сечения при 0≤ z ≤H) показаны на рисунке 1.29, а. Как следует из этих эпюр, на верхнем участке и на части нижнего участка σ_m превышает σ_t и, таким образом, здесь σ₁=σ_m , σ₂=σ_t и σ₃=0. Далее σ_m и σ_t «меняются ролями». Чтобы найти значение z1 при котором меридиональное напряжение равно окружному, приравняем правые части выражений σ_mII и σ_tII, что приведет к уравнению 4z₁-3H=0, откуда z₁=0,75H. Следовательно, σ_m = σ_t в точке экстремума эпюры σ_m.

На основе эпюр σ_m и σ_t и проведенного анализа строим эпюры главных напряжений (рисунок 1.29, б). Поскольку расчет ведется по третьей теории прочности и так - как σ₃ = 0, то эпюра σ₁ одновременно является эпюрой σ_эквIII.(σ_эквIII=σ₁-σ₃=σ₃).

Как видно, эквивалентное напряжение принимает максимальное значение на расстоянии 0,5H от вершины конуса.

Из условия прочности

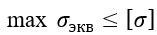
или

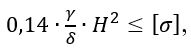
откуда

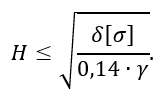
Подставив числовые значения, получим

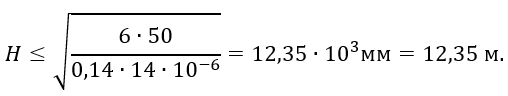
Итак, Н > Н_o (H_o = 9,0 м), т. е. допускаемый уровень поверхности жидкости больше высоты резервуара.

Этот результат, хотя формально и лишен смысла, практически означает, что резервуар может быть залит полностью, и при этом будет работать с небольшой недогрузкой. Заметим, что обычно требуемую по условию прочности толщину стенки резервуара увеличивают на 1,5 – 2,5 мм с учетом ее возможного ослабления в результате коррозии материала. Если с учетом сказанного принять в данной задаче расчетную толщину стенки на 2 мм меньше заданной, т. е. δ = 4 мм, то получим H = 10,1 м. Вывод о возможности заливки резервуара до верхней кромки остается в силе.

Пример 5. Определить минимально необходимую толщину стенки резервуара (рисунок 1.30), применив четвёртую теорию прочности. Принять [σ] = 300 кГ/ см²(30 МПа). Удельный вес жидкости, налитой в резервуар, γ = 0,9·10-3 кГ/см³(9000 Н/м³минеральное масло).

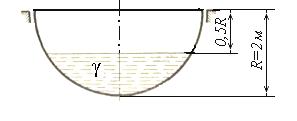
Рисунок 1.30 – Параметры резервуара

Решение. Требуемая толщина стенки определится из условия прочности составленного для опасной точки стенки резервуара. Положение «опасной» точки установим, проанализировав эпюры напряжений.

Для определения меридиональных напряжений, возникающих в стенках резервуара, будем проводить нормальные конические сечения (рисунок 1.31, а). В качестве независимой переменной примем угол φ. Радиус r основания сферического сегмента, полученного после отбрасывания верхней части резервуара (рисунок 1.31, б, в), связан с радиусом сферы зависимостью

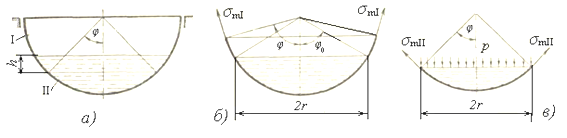
а) положение произвольного нормального конического сечения; б) сечение выше уровня поверхности жидкости; в) сечение ниже уровня поверхности жидкости

Рисунок 1.31 – Расчётные схемы

Составим уравнение равновесия для нижней отсеченной части, когда сечение проведено выше уровня свободной поверхности жидкости (рисунок 1.31, б)

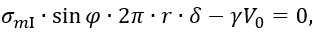
где γ V₀ – вес всей жидкости, залитой в резервуар,

V₀ – объем соответствующего сферического сегмента.

Формула для объема сферического сегмента имеет вид

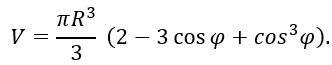
Учитывая, что согласно исходным данным cos φ_о = 0,5, получаем

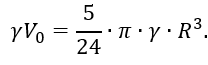
Подставляя далее V_o и r в уравнение равновесия, придем к уравнению

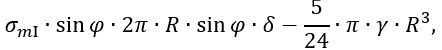
откуда

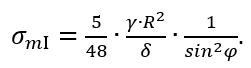
Для участка II (рисунок 1.31, в) уравнение равновесия имеет вид

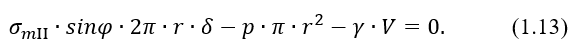
Здесь p – гидростатическое давление на глубине h (рисунок 1.31, а)

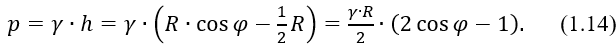
Подставляя выражения для r, р и V в уравнение равновесия нижнего участка, получаем

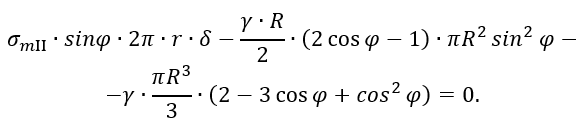
Выражая отсюда σ_mII и производя несложные преобразования, придем к формуле

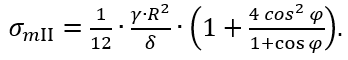
Выражения для окружных напряжений получим из уравнения Лапласа, которое для сферической оболочки имеет вид

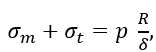
Поскольку

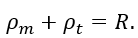
Подставляя в уравнение (1.16) на верхнем участке р = 0 и σ_mI согласно выражению (1.12), а на нижнем р и σ_mII согласно выражениям (1.14) и (1.15), получаем зависимость для σ_t.

Окончательно имеем следующие формулы для определения меридиональных и окружных напряжений:

для участка I (при 60°≤ φ ≤90°)

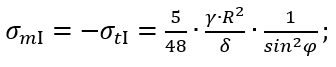
для участка II (при 0≤ φ ≤60°)

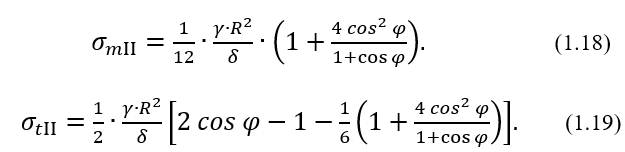
Полагая согласно исходным данным R= 2 м и γ=0,9∙10^-3 кГ/см³=9000 Н/м³, по приведенным соотношениям построим эпюры σm и σt (рисунок 1.32, а) и затем эпюры главных напряжений (рисунок 1.32, б, в).

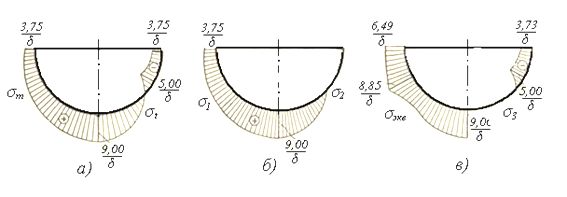
а) эпюры σ_m и σ_t; б) эпюры главных напряжений σ₁ и σ₂; в) эпюры эквивалентного σ_экв и главного σ₃ напряжений

Рисунок 1.32 – Эпюры напряжений

При построении эпюр главных напряжений, как обычно, принимаем, что радиальные напряжения равны нулю. Тогда на участке, где σ_t<0, главные напряжения равны: σ₁=σ_m, σ₂=0 и σ₃=σ_t.

Там же, где σ_t >0, роль σ₂ начинает играть σ_t, а σ₃= 0. Строим эпюру эквивалентных напряжений σ_эквIV, используя эпюры главных напряжений и применяя формулу

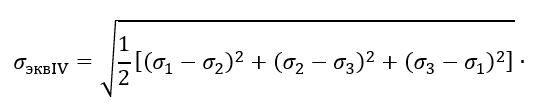
Как следует из этой эпюры (рис. 1.29, б), σ_эквIV максимально для нижней точки резервуара. Условие прочности имеет вид

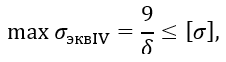
откуда

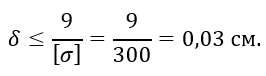
С добавкой на ослабление стенки в результате коррозии следует принять δ = 3 мм.