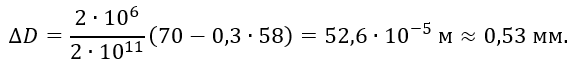Дано:

• D = 2 м
• h₁ = 1 м
• h₂ = 4 м
• h₃ = 1 м
• h₄ = D/2 = 1 м
• Удельный вес жидкости γ = 24 × 10³ Н/м³
• Давления p₀ = 20 × 10³ Н/м², p₁ = 8 × 10³ Н/м², p₂ = 10 × 10² Н/м²
• [σ] = 160 МПа
• E = 2 × 10¹¹ Па
• μ = 0,3
• (Рисунок 2.6, а)

Требуется:

1. Определить окружные σ_t и меридиональные σ_m напряжения на всех участках сосуда и построить их эпюры.
2. Определить толщину стенки сосуда δ_III из расчета на прочность по гипотезе максимальных касательных напряжений и для сравнения δ_IV по гипотезе удельной энергии формоизменения.
3. Определить площадь A поперечного сечения подкрепляющего распорного кольца по месту стыка цилиндрической части сосуда с конической.
4. Вычислить изменения диаметра сосуда ΔD на уровне h₂/2.

Расчёт

При расчёте собственный вес сосуда не учитывать.

1.1 Определение реакций креплений на сосуд

Из условия равновесия сил, действующих на сосуд, из уравнения Σу=0 (рисунок 2.6, а), учитывая, что R_A = R_B, получим

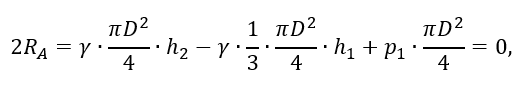
откуда

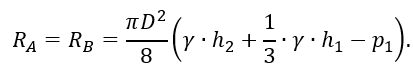
Подставив заданные величины, вычислим

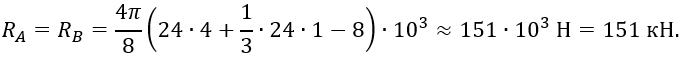
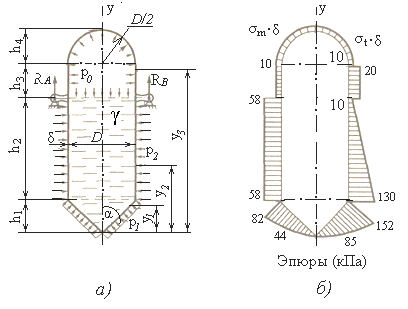
а) геометрические параметры и нагрузки; б) эпюры продольных сил в стенках сосуда

Рисунок 2.6 –

1.2 Определение окружных σ_t(y₁) и меридиональных σ_m(y₁) напряжений на уровне y₁ конической части сосуда (рисунок 2.7).

На этом участке: 0 ≤ y₁ ≤ h₁. Так как ρ_m = ∞, то по формуле Лапласа

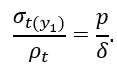
Из геометрии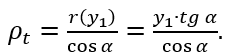

Нормальное давление на уровне y₁

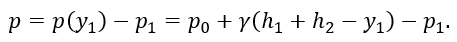
Тогда окружные напряжения

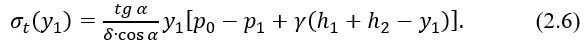
Меридиональные напряжения на том же уровне y₁ определим из условия равновесия нижней отсеченной части сосуда (рисунок 2.7)

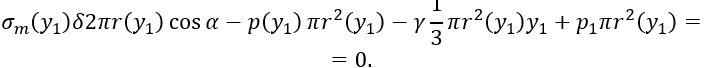
Отсюда

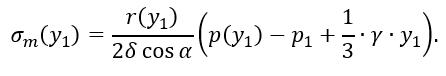
Подставив значения p(y₁) и r(y₁)=y₁∙tg α, получим

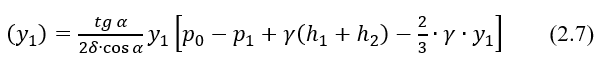
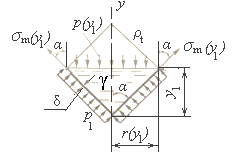
Рисунок 2.7 –

Из формул (2.6) и (2.7) видно, что в конической части сосуда σ_t и σ_m изменяются по параболическому закону. Простой анализ показывает, что экстремальные значения σ_t и σ_m находятся за пределами h₁. Поэтому, для построения эпюр σ_t и σ_m на этом участке, вычислим напряжения в трех сечениях по образующей конуса.

Для этого предварительно подставим в формулы (2.6) и (2.7) заданные значения p₀; p₁; γ; h₁; h₂ и одновременно учтем, что

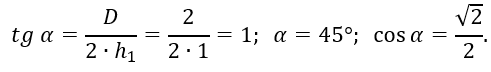
После подстановки получим

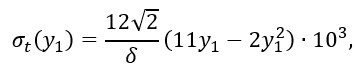
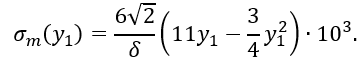
При y₁ = 0, σ_t = 0, и σ_m = 0,

при y₁ = h₁/2 = 0,5 м, σ_t = 85/δ кПа, σ_m ≈ 44/δ кПа,

при y₁ = h₁ = 1 м, σ_t = 152/δ кПа, σ_m = 82/δ кПа.

При построении эпюр σ_t и σ_m эти значения откладываем перпендикулярно образующей конуса.

Примечание. Если нижнее днище сосуда является полусферическим, то объем отсеченной на уровне y₁ части полусферы (рисунок 2.8), то-есть сферического сегмента, равен

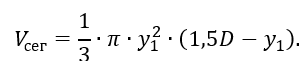
Рисунок 2.8 Расчётная схема в произвольном сечении полусферического участка

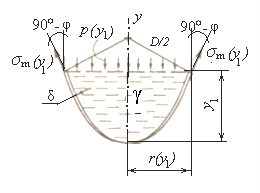
Рисунок 2.8 – Расчётная схема в произвольном сечении полусферического участка

Для сферы 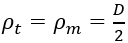и по формуле Лапласа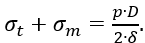

Из условия равновесия нижней отсеченной части (рисунок 2.8) меридиональные напряжения (для контроля)

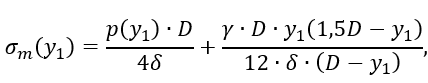
а из формулы Лапласа

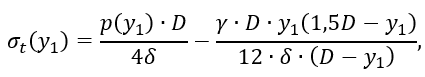
где p(y₁) – только внутреннее давление в сосуде на уровне y₁

1.3 Определение напряжений в цилиндрической части сосуда ниже уровня крепления

На этом участке: h₁ ≤ y₂ ≤ (h₁ + h₂), ρ_m = ∞, ρ_t = D/2.

По формуле Лапласа

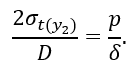
Нормальное к стенке сосуда давление р на уровне y₂ (рисунок 2.9)

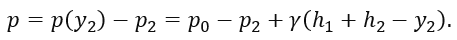
Тогда

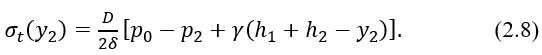
Меридиональные напряжения на том же уровне у2получим из рассмотрения равновесия нижней отсеченной части сосуда (рисунок 2.9)

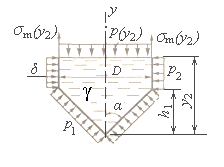
Рисунок 2.9 – Расчётная схема в произвольном сечении цилиндрического участка

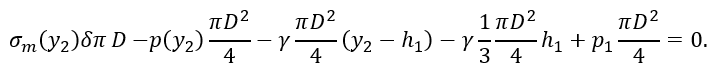
Подставляя значение внутреннего давления p(y₂)=p₀+γ(h₁+h₂-y₂ ) и произведя сокращения, получим

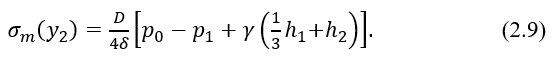
Из формул (2.8) и (2.9) видно, что в нижней части цилиндрической формы сосуда σ_m=const, а σ_t, изменяется по линейному закону. В эти формулы подставим исходные данные и вычислим значения напряжений

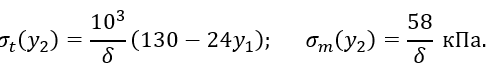
При y₂=h₁=1 м,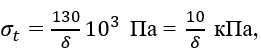

при y₂=h₁+h₂=5 м,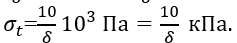

1.4 Цилиндрическая часть сосуда выше уровня жидкости, где (h₁+h₂ )≤y₁≤(h₁+h₂+h₃ ), подвергается только внутреннему давлению газа с постоянной интенсивностью р₀ (рисунок 2.6, а). На этом участке: ρ_t=D/2, ρ_m=∞ и по формуле Лапласа

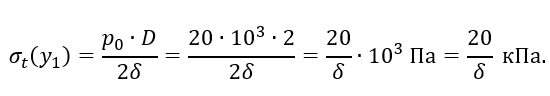
Из условия равновесия верхней отсеченной части

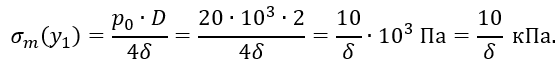
1.5 В полусферической части сосуда действует равномерное давление р₀. Для этой части p_t=p_m=D/2 и по формуле Лапласа

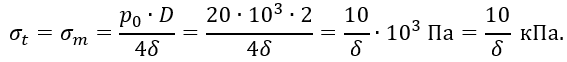
По вычисленным на всех участках значениях напряжений построены эпюры погонных нормальных сил σ_t δ и σ_m δ (рисунок 2.6, б). Эти эпюры должны быть расположены рядом с общей схемой тонкостенного сосуда. По одну сторону от оси симметрии y показана эпюра σ_t δ, по другую – эпюра σ_m δ.

1.6 Определение толщины стенки сосуда. По эпюрам σ_t δ и σ_m δ (рисунок 2.6, б) видно, что наиболее напряженными являются точки конической части сосуда по месту стыка с цилиндрической частью. В этих точках (рисунок 2.10) возникает сложное напряженное состояние, причем

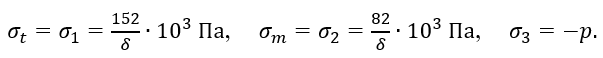
При расчете на прочность не будем учитывать влияние р ввиду его малости по сравнению с напряжениями σ_t и σ_m.

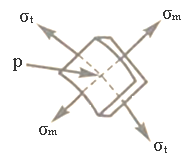
Рисунок 2.10 – Напряжённое состояние в элементе сосуда

Тогда, считая напряженное состояние плоским из условия прочности по гипотезе максимальных касательных напряжений (III гипотеза прочности)

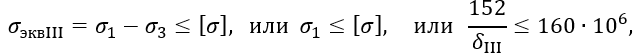
откуда толщина стенки по этой гипотезе

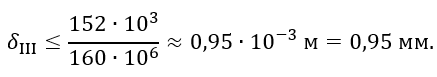
Для сравнения по гипотезе удельной энергии формоизменения (IV гипотеза прочности) при плоском напряженном состоянии, полагая σ₃≈0,

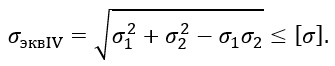
Подставив значения напряжений, получим

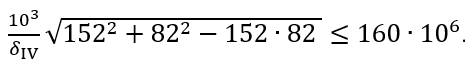
Тогда толщина стенки сосуда δ_IV≥0,825∙10^-3≈0,83 мм.

Различие толщины стенки из расчета по Ш и IV гипотезам составляет примерно 13%. Окончательный размер δ практически выбирается с учетом конструктивных особенностей сосуда и условий его эксплатации. В нашем случае примем δ = 1 мм.

1.7 Площадь A поперечного сечения подкрепляющего распорного кольца по месту стыка конической и цилиндрической частей сосуда, определим из расчета на прочность кольца от равномерной радиальной нагрузки q₀=σ₀∙δ=σ_m^к∙δ∙sin⁡α (рисунок 2.5, а).

Нормальная сжимающая сила в любом поперечном сечении кольца (рисунок 2.11)

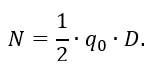
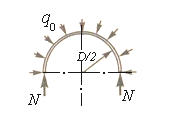
Рисунок 2.11 – Расчётная схема в произвольном сечении кольца

По условию прочности

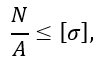
откуда

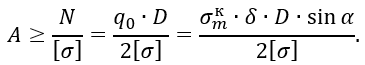
Подставив числовые значения, получим

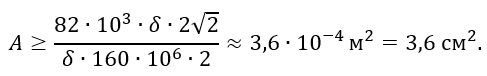
Полученные из условий прочности размеры толщины стенки сосуда δ и площади А распорного кольца обычно проверяются расчетом на устойчивость.

1.8 Изменение диаметра ΔD цилиндрической части сосуда на уровне h₁/2, т. е. вдали от краевого эффекта.

Обозначим диаметр сосуда после деформации через D1.

Тогда окружная деформация сосуда

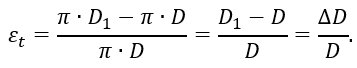
При плоском напряженном состоянии по закону Гука

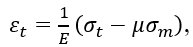
где E=2∙10¹¹ Па – модуль продольной упругости материала,

μ – коэффициент Пуассона.

Следовательно,

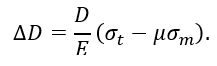
На уровне h₁/2 из эпюр напряжений (рисунок 2.6, б) при толщине стенки δ = 1 мм = 10^(-3) м, имеем

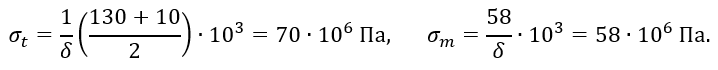
Тогда изменение диаметра