План:

1.Источники и классификация погрешностей результата численного решения задачи.

2. Абсолютная и относительная погрешность.

3. Корректность.

---

1) Для правильного понимания подходов и критериев, используемых при решении прикладной задачи с применением ЭВМ, очень важно с самого начала признать, что получить точное значение решения практически невозможно и не в этом цель вычислений. Получаемое на ЭВМ решение у почти всегда (за исключением некоторых весьма специальных случаев) содержит погрешность, т.е. является приближенным. Невозможность получения точного решения следует уже из ограниченной разрядности вычислительной машины.

Наличие погрешности решения обусловлено рядом весьма глубоких причин.  Есть четыре источника погрешности результата. Перечислим их.

1°. Математическая модель является лишь приближенным описанием реального процесса. Характеристики процесса, вычисленные в рамках принятой модели, заведомо отличаются от истинных характеристик, причем их погрешность зависит от степени адекватности модели реальному процессу.

2°. Исходные данные, как правило, содержат погрешности, поскольку они либо получаются в результате экспериментов (измерений), либо являются результатом решения некоторых вспомогательных задач.

3°. Применяемые для решения задачи методы в большинстве случаев являются приближенными. Найти решение возникающей на практике задачи в виде конечной формулы возможно только в отдельных, очень упрощенных ситуациях.

4°. При вводе исходных данных в ЭВМ, выполнении арифметических операций и выводе результатов на печать производятся округления.

2) Абсолютная и относительная погрешности.

Пусть а — точное (вообще говоря, неизвестное) значение некоторой величины, а* — известное приближенное значение той же величины (приближенное число). Ошибкой (или погрешностью) приближенного числа а называют разность  между точным и приближенным значениями.

Простейшей количественной мерой ошибки является абсолютная погрешность

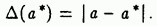
Однако по величине абсолютной погрешности далеко не всегда можно сделать правильное заключение о качестве приближения. Вводится понятие относительной погрешности 

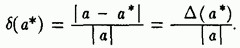
Использование относительных погрешностей удобно, в частности, тем, что они не зависят от масштабов величин и единиц измерения.

Более реальная и часто поддающаяся решению задача состоит в получении оценок погрешности вида

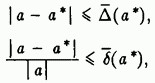
Замечание. В литературе по методам вычислений широко используется термин "точность". Принято говорить о точности входных данных и решения, о повышении и снижении точности вычислений и т.д. Мы также будем использовать эту терминологию, за которой скрывается довольно простой смысл. Точность в качественных рассуждениях обычно выступает как противоположность погрешности, хотя для количественного их измерения используются одни и те же характеристики (например, абсолютная и относительная погрешности). Точное значение величины — это значение, не содержащее погрешности. Повышение точности воспринимается как уменьшение погрешности, а снижение точности — как увеличение погрешности. Часто используемая фраза "требуется найти решение с заданной точностью означает, что ставится задача о нахождении приближенного решения, принятая мера погрешности которого не превышает заданной величины. 

3. Задача у=A(х) называется корректно поставленной, если для любых входных данных х из некоторого класса решений существует у, единственно и устойчиво ко входным данным. Отсутствие устойчивости означает, что даже небольшой погрешности х соответствует весьма большая погрешность решения у.

Литература [2], [3], [4], [13].