6. Методы расчета строительных сооружений

План:

1. Метод конечных разностей.

2. Метод конечных элементов.

1) При решении задач методом конечных разностей  (МКР)   точное значение производных в дифференциальных уравнениях заменяются их приближенными значениями через конечные разности или дискретные значения функций. Задача сводится к решению системы алгебраических уравнений.

 Пусть дана функция двух переменных F=F(x,y). Аппрроксимируем рассматриваемую область прямоугольной сеткой с шагом Δx=λx , Δу=λу (рисунок 1.1).

Вычислим частную производную 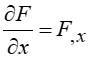в узле i.

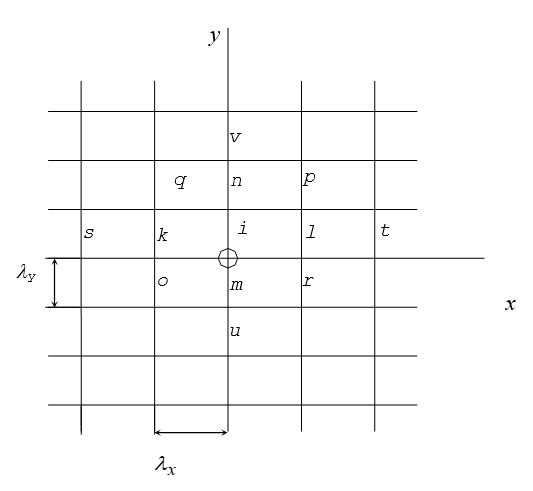
Рисунок 1.1

В узле i построим касательную АВ к поверхности F = F(x,y) (рисунок 1.2). Известно, что точное значение производной F,x равно тангенсу угла наклона (tgα) касательной к оси  х. Для получения приближенного значения призводной F,x касательную АВ заменим секущей А1В1,тангенс угла наклона которой к оси  х есть приближенное представление первой производной  F,x в узле i.

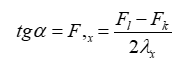(1.1)

По аналогии представляем частную производную F,y в конечных разностях

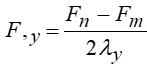(1.2)

где λх– шаг сетки в направлении оси х, λy– шаг сетки в направлении оси у.

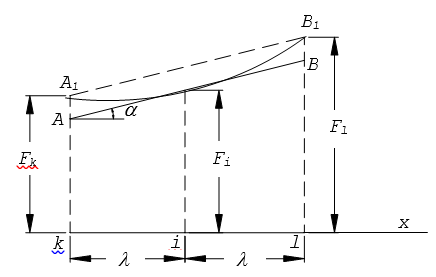
Рисунок 1.2

Вторые производные получим путем замены числителя разностью первых разностей, а в знаменатель запишем квадрат соответствующего шага сетки

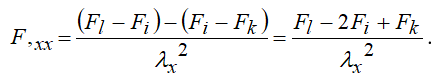(1.3)

По аналогии получаем вторые производные по у

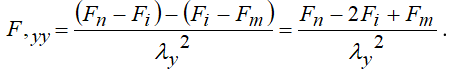(1.4)

Рассуждая аналогично, представим третьи производные в конечных разностях

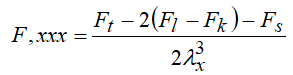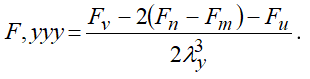(1.5) (1.6)

Для четвертых производных имеем

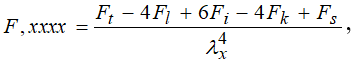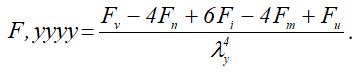(1.7) (1.8)

Наконец для смешанных производных

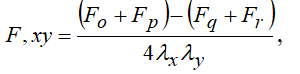(1.9) 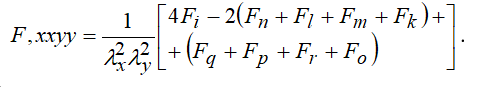(1.10)

Оператор Лапласа по двум переменным примет вид

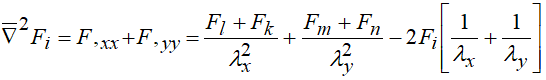(1.11)

Для случая квадратной сетки λx=λy=λ все выражения упростятся. Например, оператор Лапласа примет вид

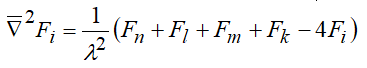(1.12)

Достоинством МКР является сравнительная с другими численными методами простота и доступность. Метод хорошо реализуется на ЭВМ. Недостатком можно считать сложности, возникающие при реализации граничных условий свободного края или наличия отверстий в оболочках и пластинах. В этих случаях для получения хороших результатов, как уже отмечалось, приходится применять нерегулируемую сетку, что приводит к усложнению программ расчета на ЭВМ.

2) Метод конечных элементов

Метод конечных элементов является универсальным численным методом, позволяющим с достаточной точностью решать задачи теории сооружений. Большие преимущества демонстрирует этот метод при расчетах конструкций сложных форм и конструкций типа пластин и оболочек.

Суть метода заключается в разделении конструкции на отдельные элементы. В МКЭ функционал энергии для всей рассматриваемой области представляется в виде суммы функционалов отдельных ее частей – конечных элементов. В пределах каждого такого элемента независимо от других элементов задается закон распределения функций, выбранных в качестве разрешающих уравнений. Расчет по методу конечных элементов начинается с дискретизации расчетной схемы. Рассматриваемые объекты расчленяют на конечные элементы. Однородные объекты  (балки, рамы, фермы) разбиваются на конечные элементы  в виде стержней, двумерные объекты (пластины, оболочки) рекомендуется разбивать на треугольные или прямоугольные конечные элементы, массивы (трехмерные тела) конечные элементы принимаются в виде параллелепипеда или тетраэдра.

Расчет методом конечных элементов выполняется в следующей последовательности:

1. Составить дифференциальные уравнения равновесия или функционал;

2. Произвести дискретизацию объекта, расчленив его на конечные элементы;

3. Произвести аппроксимацию переменных на одном конечном элементе через значения переменных в выбранном узле;

4. Построить матрицу жесткости и привести местную нагрузку к узловой;

5. Составить канонические уравнения;

6. Решить систему канонических уравнений и определить значения неизвестных величин;

7. Определить компоненты напряженно-деформированного состояния (деформации, напряжения) по конечному элементу в произвольных заранее заданных местах.

Литература [2], [3], [4], [13].