План:

1. Матричная форма решения систем уравнений.

2. Решение систем уравнений методом простых итераций.

3. Решение систем уравнений методом Гаусса-Зейделя.

---

Задания:

Задание №1 Решить систему матричным методом

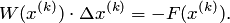
Задание №2 Найти решение системы 4 линейных уравнений с 4-мя неизвестными x₁, x₂, x₃, x₄ с точностью до 10^-4 методом простой итерации;

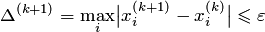
Ответ:

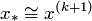
Задание №3 Методом Зейделя решить систему (точность 0,01)

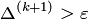
Ответ: (0,752; 1,289; -0,005)

Алгоритм метода Зейделя

1. Преобразовать систему Ax=bк виду x=αx+β одним из описанных способов.

2. Задать начальное приближение решения x⁽⁰⁾произвольно или положить x⁽⁰⁾=β, а также малое положительное число ε(точность). Положить k=0.

3. Произвести расчеты по формуле (10.15) или (10.16) и найти x^(k+1).

4. Если выполнено условие окончания ||x^(k+1)-x^(k)||<ε, процесс завершить и в качестве приближенного решения задачи принять x_*≈ x^(k+1). Иначе положить k=k+1и перейти к пункту 3.

Программа для решения СЛАУ методом Гаусса-Зейделя приведена ниже. Поскольку при некорректной постановке задачи количество итераций может стать излишне большим, в программе предусмотрено прекращение итерационного процесса при превышении заранее заданного предельного числа итераций.

Литература [2], [3], [8], [10].