План:

1.Составление алгоритма решения задачи.

2.Решение практических задач по теме занятия.

---

Задания:

В качестве примера рассмотрим задачу о плоском изгибе призматического стержня (рисунок 1.4, а). Дифференциальные уравнения изогнутой оси балки содержат четвертую производную от функции прогиба :

Так как функцию прогиба необходимо дифференцировать четыре раза придадим ей  кубическую зависимость от координаты:

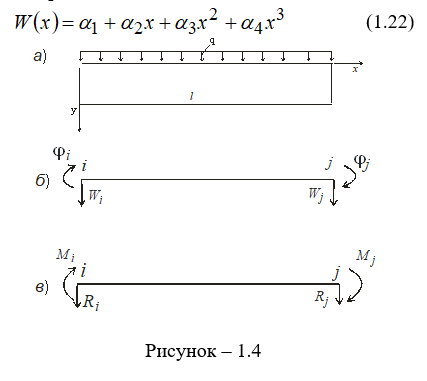
Конечный элемент стержня имеет два узла i, j, каждому из которых приданы две степени свободы (рисунок 1.4,б). Причем здесь степени свободы имеют следующий физический смысл:

W_i, φ_i – вертикальное перемещение узла i;

W_j, φ_j– вертикальное перемещение и угол поворота узла j.

Для определения неизвестных коэффициентов α уравнения (1.22) выразим их через значения степеней свободы (W_i,j, φ_i,j). Запишем граничные условия задачи:

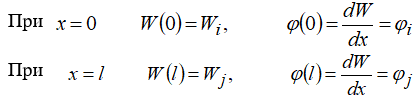
Подставим граничные условия в уравнение (1.22) и получим систему алгебраических уравнений

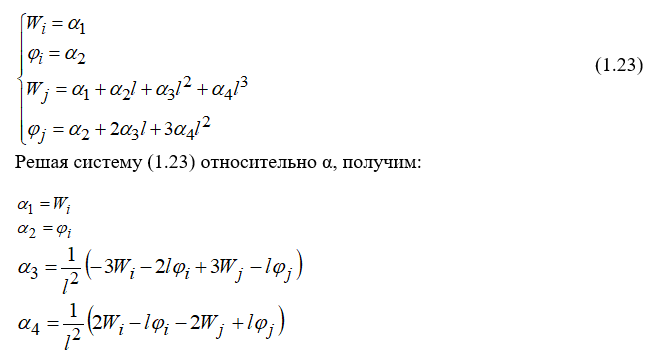
Подставим эти коэффициенты в полином (1.22) и преобразуем его, собирая коэффициенты при неизвестных . В результате получим:

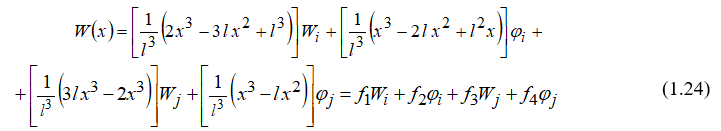
Функции (1.24) описывают распределение перемещений по области изгибаемой балки, когда одно из перемещений равно единице, а остальные равны нулю (рисунок 1.5).

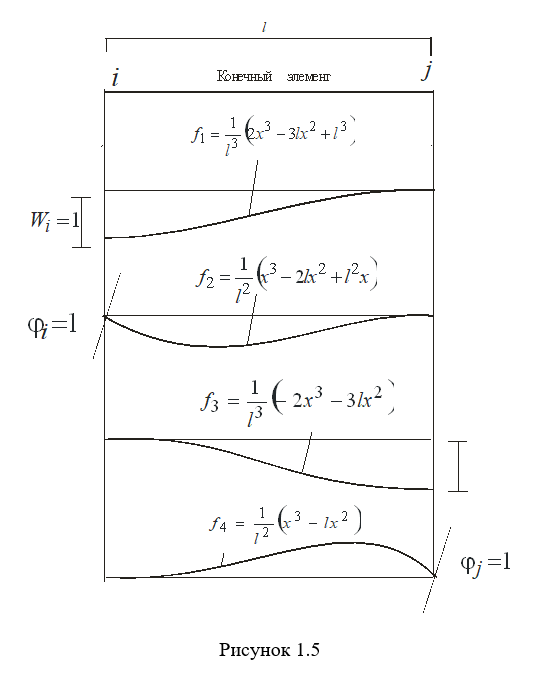
Определенному деформированному состоянию элемента соответствует его напряженное состояние. Если деформированное состояние конечного элемента характеризуется вектором перемещений 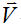с компонентами:

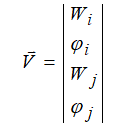
то соответствующее напряженное состояние определяется вектором узловых реакций конечного элемента

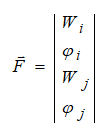
В упругой стадии деформирования между реакциями связей и узловыми перемещениями существует линейная зависимость

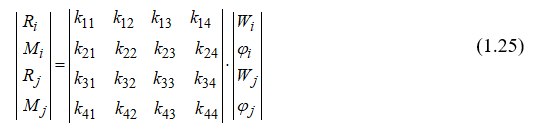
Выражение (1.25) можно записать в более компактном виде:

где 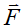– вектор узловых реакций (сил) конечного элемента;

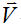– вектор узловых перемещений;

K – матрица жесткости (реакции) конечного элемента, выражающая зависимость между векторам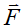и  и.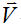

Умножая первую строку матрицы K на вектор-столбец 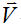, получим значение поперечной силы (или реакции) в узле  от всевозможных компонентов деформированного состояния

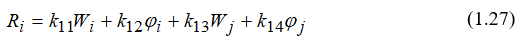
где   k_αβ – коэффициенты жесткости α,β=1,2,3. Физический смысл коэффициентов k_αβ вытекает из соотношения (1.27) как усилие в узле α, возникающее от единичного перемещения по направлению, которое определено индексом β, если все остальные перемещения равны нулю. Выражения вида (1.27) можно аналогично записать для остальных трех компонентов вектора узловых сил КЭ – M_i, M_j, R_j.

Значения коэффициентов можно получить различными методами сопротивления материалов или строительной механики стержневых систем. Например, для определения R_j надо придать единичные значения последовательно перемещениям W_i,j, φ_i,j и суммировать возникшие при этом реакции по направлению

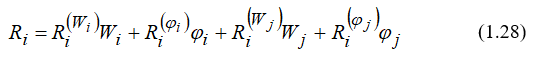
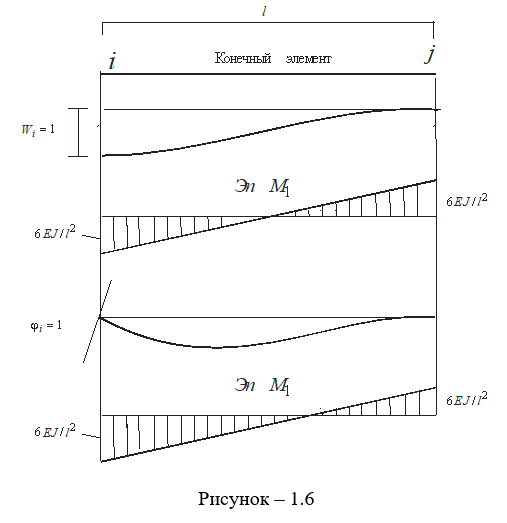
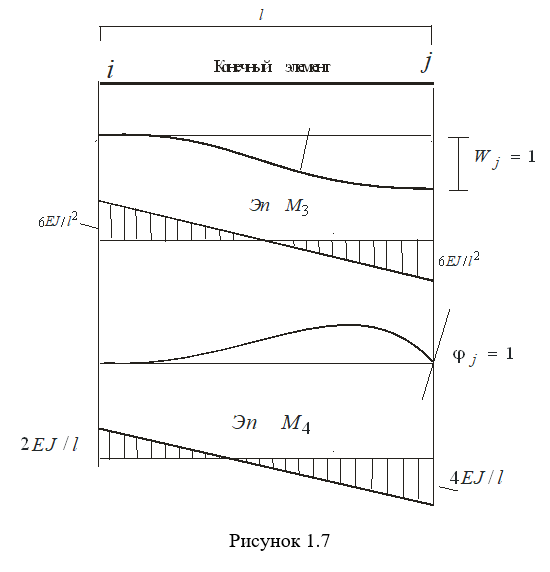
Рассмотрим наиболее общий случай напряженного состояния, соответствующий наиболее общему случаю деформирования. Таким является конечный элемент с защемленными краями, в котором возникают все компоненты 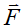. На рисунках 1.6 и 1.7 показаны эпюры моментов и значения опорных реакций от 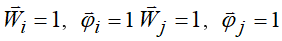. Запишем теперь (1.28) с конкретными значениями

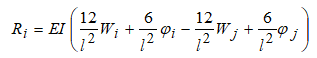
Или в матричной форме

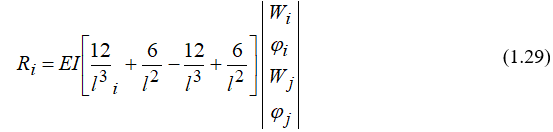
Рассуждая аналогично (1.28) и (1.29) можно установить связь  и  для всего конечного элемента согласно принятым степеням свободы

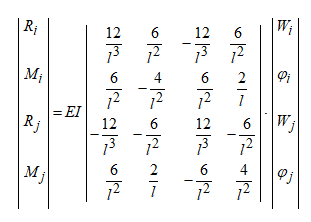
Приведение распределенной нагрузки к узловой выполняется аналогично подобной операции для ферм.  Так, для равномерно распределенной нагрузки с интенсивностью q имеем:

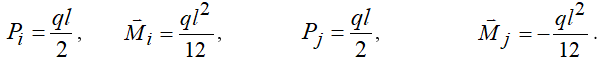
здесь 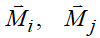представляет собой сосредоточенные моменты, приложенные в узлах конечного элемента.

Решение задач по карточкам, выдаваемым преподавателем

Литература [2], [3], [7], [8], [10].