4. Методы решения систем нелинейных уравнений
План:
1. Метод Ньютона.
2. Метод простых итераций.
3. Метод Зейделя.
Общего аналитического решения системы нелинейных уравнений не найдено. Существуют лишь численные методы.
1) Метод Ньютона- наиболее популярный численный метод решения систем нелинейных уравнений. Он предусматривает выделение из уравнений системы линейных частей, которые играют определяющую роль при малых приращениях аргументов. В результате решение системы нелинейных уравнений сводится к решению последовательности систем линейных уравнений.
Рассмотрим нелинейную систему уравнений
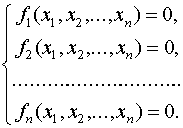(1)
с действительными левыми частями. Систему (1) можно представить в матричном виде
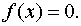(2)
Здесь приняты следующие обозначения:
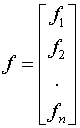- вектор аргументов, а 
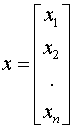- вектор – функция.
Для решения системы (2) воспользуемся методом последовательных приближений.
Предположим, что найдено р-ое приближение xp = (x1(p), x2(p) , ..., xn(p)) одного из изолированных корней x = (x1, x2, x3, ..., xn) векторного уравнения (2). Тогда точный корень уравнения (2) можно представить в виде
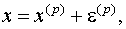(3)
где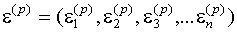 
- поправка (погрешность) корня на n – ом шаге.
Подставив выражение ( 3) в ( 2), получим
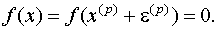(4)
Предположим, что функция f(x) - непрерывно дифференцируема в некоторой выпуклой области, содержащей x и x(p). Тогда левую часть уравнения (4) разложим в ряд Тейлора по степеням малого вектора ε(p), ограничиваясь линейными членами:
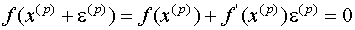(5)
или в развернутом виде:
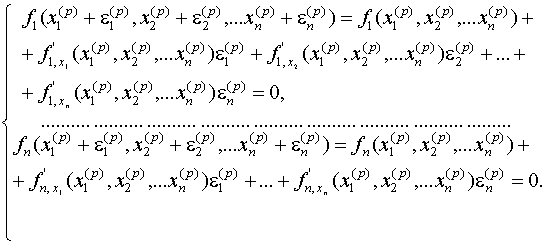(6)
Из анализа формул (5) и (6) следует, что под производной f¢ (x) следует понимать матрицу Якоби системы функций f1 , f2, ..., fn, относительно переменных x1, x2, x3, ..., xn, то есть:
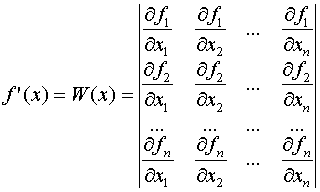(7)
Выражение (7) в краткой записи можно представить:
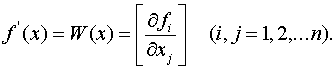(8)
Выражение (6) представляет собой линейную систему относительно поправок εi(p) (i = 1, 2, ..., n) с матрицей W
/I>(x), поэтому формула (5.5) может быть записана в следующем виде:
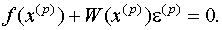(9)
Отсюда, предполагая, что матрица W(x(p)) - неособенная, получим:
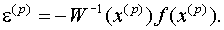(10)
Теперь, подставив выражение (10) в формулу (3), окончательно получим:
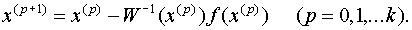(11)
Таким образом, получили вычислительную формулу (метод Ньютона), где в качестве нулевого приближения x(0) можно взять приближенное (грубое) значение искомого корня.
К недостаткам метода Ньютона следует отнести:
– необходимость задавать достаточно хорошее начальное приближение;
– отсутствие глобальной сходимости для многих задач;
– необходимость вычисления матрицы Якоби на каждой итерации;
– необходимость решения на каждой итерации системы линейных уравнений, которая может быть плохо обусловленной.
Достоинством метода является квадратичная сходимость из хорошего начального приближения при условии невырожденности матрицы Якоби.
2) Метод простых итераций.
Метод простых итераций для решения (1) аналогичен методу, рассмотренному при решении нелинейных уравнений с одним неизвестным. Прежде всего, выбирается начальное приближение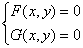 
, а исходная система уравнений преобразуется к эквивалентной системе вида
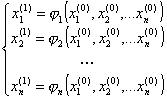(5)
и по ней осуществляется итерационный цикл. Если итерации сходятся, то они сходятся к решению уравнения (1). Обозначим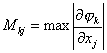 
. Достаточным условием сходимости является ||M||<1. Скорость сходимости метода сильно зависит от вида конкретно подбираемых функций φi, которые должны одновременно удовлетворять условиям эквивалентности (5) и (1), и обеспечивать сходимость итерационного процесса.
Например, для исходной системы уравнений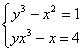 
эквивалентная итерационная система (5) может быть представлена в следующем виде:
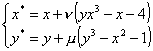
где множители μ = –0.15 и ν = –0.1 подбираются из анализа условий сходимости.
3) Порядок применения методов простых итераций и Зейделя
Исходная система преобразуется к эквивалентному виду: xi=φi(x1,x2,…,xn), i = 1,2,...,n (из одного уравнения выражается x1, из другого – x2 и т.д.). Выбираются начальные значения неизвестных: x1(0), i=1,2,...,n и реализуется итерационный процесс вычисления приближений к решению системы по правилам:
метод простых итераций - xi(k+1)=φi(x1(k),x2(k),…,xn(k)), k=0,1,2,...; i=1,2,...,n;
метод Зейделя - xi(k+1)=φi(x1(k+1),…, xi-1(k+1), xi(k),…,xn(k)), k=0,1,2,...; i=1,2,...,n.
Условие прекращения процесса:
для систем нелинейных уравнений – maxi=1,…,n{| xi(k+1)- xi(k) |}<ε (e – заданная точность решения), при этом xi*≈xi(k+1), i = 1,2,...,n.
Отличие метода Зейделя от метода простых итераций: при вычислении x2(k+1) вместо x1(k) используется только что вычисленное значениеx1(k+1); x3(k+1) вычисляется уже с использованием вычисленных в текущей итерации значений x1(k+1), x2(k+1) и т.д. Такой прием позволяет увеличить скорость сходимости итераций. Преимущество метода Зейделя в скорости тем больше, чем больше порядок рассматриваемой системы.
Достаточное условие сходимости итерационных процессов:
1) функции φi(x1,x2,…,xn), i=1,2,...,n определены и непрерывно дифференцируемы в некоторой окрестности решения системы;
2) начальное xi(0), i=1,2,…n и все вычисляемые приближения к решению системы находятся в этой окрестности;
3) во всех точках окрестности одновременно выполняются неравенства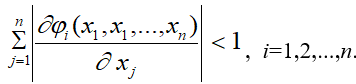 
Литература [2], [3], [4], [13].