3. Методы решения систем линейных уравнений
План:
1. Задачи линейной алгебры.
2. Матричная форма решения систем уравнений.
3. Метод простых итераций.
4. Метод Гаусса-Зейделя.
1) В общем случае система линейных уравнений, содержащая m уравнений и n переменных имеет вид:
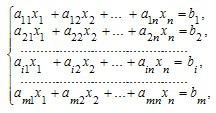
Здесь m — количество уравнений, n — количество переменных, x1 ,x2… ,x n _ — неизвестные, которые надо определить коэффициенты a11,a12,… ,a mn и свободные члены b1, b2,… ,bm _ предполагаются известными. Индексы коэффициентов в системах линейных уравнений (a ij ) формируются по следующему соглашению: первый индекс ( i) обозначает номер уравнения, второй ( j) — номер переменной, при которой стоит этот коэффициент
Решение систем линейных алгебраических уравнений — одна из классических задач линейной алгебры, во многом определившая её объекты и методы. Кроме того, линейные алгебраические уравнения и методы их решения играют важную роль во многих прикладных направлениях, в том числе в линейном программировании,
Решением системы уравнений называется такой n-мерный вектор Х = (x1, x2,...,xn), который одновременно является решением каждого из уравнений системы.
Системы уравнений бывают:
Равносильными называются две системы уравнений, если они имеют одно и тоже множество решений.
Совместной называется система уравнений, если она имеет хотя бы одно решение.
Несовместной называется система уравнений, если она не имеет ни одного решения.
Определенной называется система уравнений, если она имеет единственное решение.
Неопределенной называется система уравнений, если она имеет бесконечное множество решений.
2) Матричная форма решения систем уравнений. Система уравнений может быть записана в векторном виде:
A1x1 + A2x2 + ... + Anxn =B
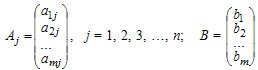
Пример 1. Записать в векторном виде.
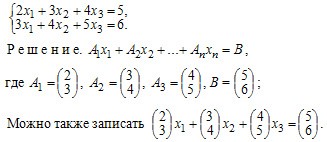
В матричной записи система линейных уравнений может быть записана следующим образом:
A · X = B,
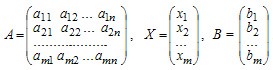
Здесь A — это матрица системы, Х — столбец неизвестных, В — столбец свободных членов. Если к матрице A приписать справа столбец свободных членов, то получившаяся матрица называется расширенной. Матричный метод применяется только для квадратных матриц (m = n ).
Запишем заданную систему в матричном виде:
AX = B.
Если матрица невырождена, то тогда с помощью операций над матрицами выразим неизвестную матрицу. Операция деления на множестве матриц заменена умножением на обратную матрицу, поэтому домножим последнее равенство на матрицу слева:
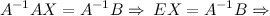
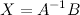
Поэтому, чтобы найти неизвестную матрицу надо найти обратную матрицу к матрице системы и умножить ее справа на вектор-столбец свободных коэффициентов.
2) Метод простых итераций.
Альтернативой прямым методам решения СЛАУ являются итерационные методы, основанные на многократном уточнении x(0), заданного приближенного решения системы A·x=b. Верхним индексом в скобках здесь и далее по тексту обозначается номер итерации (совокупности повторяющихся действий).
Реализация простейшего итерационного метода — метода простых итераций — состоит в выполнении следующих процедур.
1. Исходная задача A·x=b преобразуется к равносильному виду:
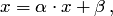
где α – квадратная матрица порядка n; β – столбец. Это преобразование может быть выполнено различными путями, но для обеспечения сходимости итераций нужно добиться выполнения условия ||α|| < 1.
2. Столбец β принимается в качестве начального приближения x(0) = β и далее многократно выполняются действия по уточнению решения, согласно рекуррентному соотношению
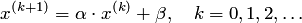
Итерации прерываются при выполнении условия (где ε > 0 – заданная точность, которую необходимо достигнуть при решении задачи)
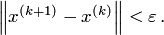
Алгоритм метода простых итераций
1. Преобразовать системуAx=bк виду x=ax+β одним из описанных способов.
2. Задать начальное приближение решенияx(0)произвольно или положить x(0) = β, а также малое положительное число ε(точность). Положить k = 0.
3. Вычислить следующее приближениеx(k+1)по формуле x(k+1)=ax(k)+β.
4. Если выполнено условие ||x(k+1)-x(k)||<ε, процесс завершить и в качестве приближенного решения задачи принятьx*≈ x(k+1). Иначе положить k=k+1и перейти к пункту 3 алгоритма.
4) Метод Гаусса-Зейделя
Данный метод является одним из самых распространенных итерационных методов решения СЛАУ, поскольку он отличается простотой и легкостью программирования. Рассмотрим его суть. Допустим, диагональные коэффициенты исходной матрицы {aij}отличны от нуля (в противном случае можно переставить местами уравнения исходной системы). Представим исходную систему
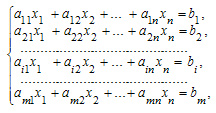
в следующем виде:
 (2.5)
(2.5)
Если теперь задать для неизвестных их начальные приближенные значения , то система (2.5) позволяет вычислить более точные значения неизвестных на первом шаге (на первой итерации):
 (2.6)
(2.6)
Используя найденные значения неизвестных, можно еще более уточнить их на второй итерации:
 (2.7)
(2.7)
и так далее.
В данном методе для нахождения значения i-го неизвестного на каждой итерации используются значения предыдущих неизвестных, уже найденные на данной итерации. Общую формулу определения i-го неизвестного на k-й итерации для системы n уравнений можно записать так:
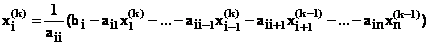 i = 1, 2, … , n; k = 1, 2, … (2.8)
i = 1, 2, … , n; k = 1, 2, … (2.8)
Итерационный процесс продолжается до тех пор, пока все значения xi(k), не станут достаточно близкими к xi(k-1). Близость этих значений можно охарактеризовать максимальной абсолютной величиной их разности . Тогда при заданной точности вычислений > 0 критерий окончания итерационного процесса можно записать в виде:
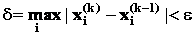 (2.9)
(2.9)
При выполнении этого условия итерационный процесс называется сходящимся. В этом случае максимальные разности между значениями соответствующих неизвестных в двух последовательных итерациях убывают, а сами значения стремятся к решению системы.
Доказано, что для сходимости итерационного процесса достаточно, чтобы модули диагональных коэффициентов для каждого уравнения были не меньше суммы модулей всех остальных коэффициентов:
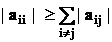
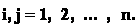 (2.10)
(2.10)
При этом хотя бы для одного уравнения неравенство (2.10) должно выполняться строго.
Литература [2], [3], [4], [13].