План:

1.Составление алгоритма решения задачи.

2. Решение практических задач по теме занятия.

---

Задания:

1) Метод Ньютона

Алгоритм метода Ньютона для решения нелинейных систем

1. Задать начальное приближение x⁽⁰⁾и малое положительное число ε (точность). Положить k=0.

2. Решить систему линейных алгебраических уравнений относительно поправки ∆x^(k).

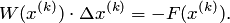
3. Вычислить следующее приближение: x^(k+1)= x^(k)+∆ x^(k).

4. Если 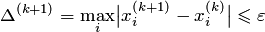, процесс закончить и положить 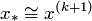. Если 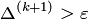, то положить 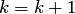и перейти к пункту 2.

Пример. Решить систему методом Ньютона

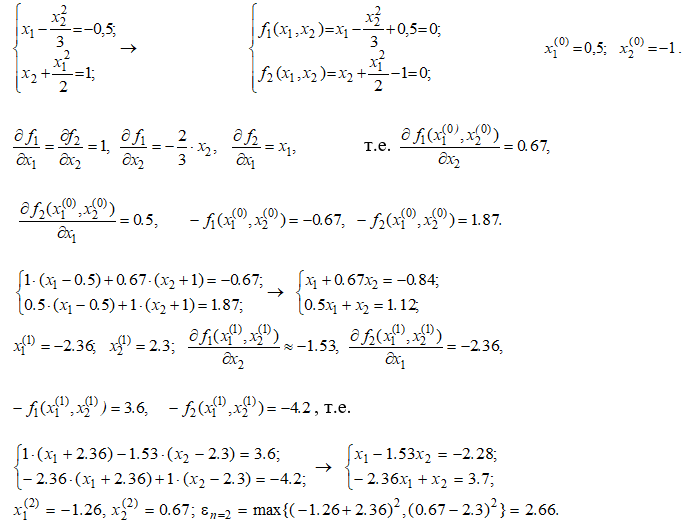
При использовании метода Ньютона для решения системы придется последовательно формировать и решать системы линейных уравнений:

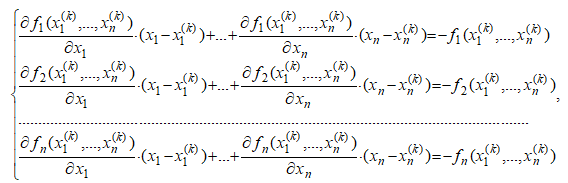
k=0, 1,…  Для их решения обычно используется метод  Гаусса-Зейделя, т.к. вероятность выполнения для всех этих систем достаточного условия сходимости итераций  весьма невелика.

2) Метод простых итераций.

Алгоритм метода простых итераций для систем

1. Задать начальное приближение 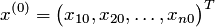 и малое положительное число ε (точность). Положить k=0.

2. Вычислить x^(k+1)по формуле

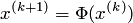
или

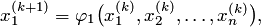
3. Если 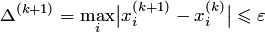, процесс завершен и 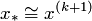. Если 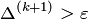, то положить 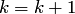и перейти к п.2.

Пример. Найти корни нелинейной системы уравнений, расположенные в первом квадранте, методом простых итераций с точностью ε = 0,001

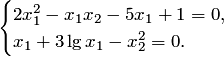
3) Метод Зейделя

1. Алгоритм метода Зейделя для решения нелинейных систем

2. Задать начальное приближение x⁽⁰⁾и малое положительное число (точность). Положить k=0.

Вычислить x^(k+1)по формулам где прямоугольниками отмечены значения, которые берутся из предшествующих уравнений на текущей итерации.

3. Если 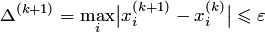, процесс завершен и 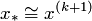. Если 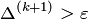, то положить 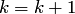и перейти к п.2.

Пример.  Решить систему методами простых итераций и Зейделя.

Решение:

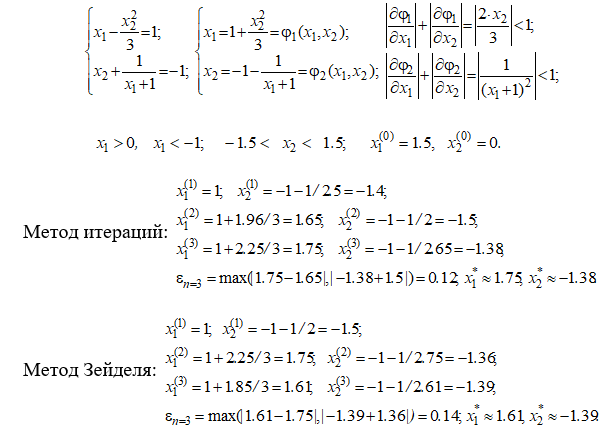
Решение задач по карточкам, выдаваемым преподавателем

Литература [2], [7], [8], [10].