2. Организация производства на основе сетевого планирования

Сетевой график представляет собой модель состоящую из стрелок и кружков с рассчитанными временными параметрами. В основе его построения лежат понятия «работа» и «событие»

Работа - это производственный процесс требующий затрат времени и материальных ресурсов и приводящий к достижению определенных результатов.

Событие - это факт окончания одной или нескольких работ необходимый и достаточный для начала следующих работ.

Начальное событие определяет начало данной работы и считается конечным для предшествующих работ.

Конечное событие определяет окончание данной работы и является начальным для последующих работ.

Исходное событие – событие которое не имеет предшествующих работ в рамках рассматриваемого сетевого графика.

Завершающее событие – событие которое не имеет последующих работ в рамках рассматриваемого сетевого графика.

Сетевые модели могут быть ориентированы на события и на работы. Наибольшее распространение получили модели ориентированные на работы. События при этом обозначаются кружками, а работы – соединяющими их сплошными стрелками.

Пунктирные стрелки обозначают фиктивные работы, имеющие нулевую продолжительность и используемые лишь для правильного отображения взаимосвязей работ в комплексе.

Путь – непрерывная последовательность работ в сетевом графике. Длину пути определяют суммой продолжительностей составляющих его работ.

Полный путь – путь от исходного до завершающего события сетевого графика.

Критический путь – полный путь, имеющий наибольшую продолжительность из всех возможных полных путей. Его длина определяет срок выполнения работ по сетевому графику.

Критические работы – это работы, лежащие на критическом пути.

Построенная с учетом технологической последовательности выполнения работ сетевая модель должна удовлетворять следующим требованиям: - иметь только одно исходное и завершающее события; - у каждой работы или технологической связи начальное событие должно иметь меньший номер чем конечное; - направление стрелок в сетевой модели следует принимать слева направо; - форма модели должна быть простой, без лишних пересечений, большинство работ следует изображать горизонтальными линиями; - при выполнении параллельных работ, когда одно событие служит началом двух или более работ заканчивающихся другим событием, вводятся фиктивные работы и дополнительные события; - при построении модели следует избегать возникновения «тупиков» и «циклов».

Тупик – это событие (кроме завершающего), из которого не выходит ни одна работа, или какое-либо событие (кроме исходного), в которое не входит ни одна работа.

Цикл характеризуется тем, что цепочка работ возвращается к тому же событию, из которого вышла.

Основными целями применения систем сетевого планирования и управления производством является разработка оптимального варианта плана и организации производства, обеспечивающих рациональную увязку во времени и пространстве выполняемых работ и наилучшее использование ресурсов, а также эффективное управление процессом реализации этого плана.

В качестве объектов сетевого моделирования в промышленном производстве могут выделяться комплексы работ по созданию отдельных наиболее сложных, либо группы механизмов, изделий или машин.

Организацию работ на основе сетевого графика рассмотрим на конкретном примере.

2.1 Расчет временных параметров организации механосборочного производства с применением сетевого моделирования

Задание. Для изготовления определенного механизма необходимо выполнить следующие работы, характеризующиеся длительностью в часах:

С учетом технологической последовательности выполнения работ построить сетевую модель организации механосборочного производства. На основе полученной сетевой модели графическим методом рассчитать временные параметры рассматриваемого комплекса работ и построить сетевой график его выполнения. Найти критический путь и выделить его на сетевом графике. При несоответствии срока окончания работ провести оптимизацию сетевого графика.

Пример расчета

С учетом технологической последовательности выполнения работ построим сетевую модель (рисунок 2.1). Событие 1 в данной модели является исходным, работы 1-2, 1-3 – исходные работы сетевой модели, выходящие из исходного события. Событие 8 – завершающее событие модели. Работа 7-8 завершающая работа, выполнением которой достигается окончание всего комплекса работ, описываемого данной сетью.

Зависимость 2-3 – организационная, она отражает необходимость одновременного завершения работ 1-2 и 1-3 и начала механической обработки деталей обоих узлов. Зависимость 6-7 технологическая. Она показывает, что для начала работы 7-8 необходимо закончить регулирование и отладку узла А.

Для работ 3-4 и 2-5 работы 1-3 и 1-2 (через зависимость 2-3) – предшествующие. Их выполнение является непосредственным условием начала работ 3-4 и 2-5. Работа 7-8 последующая. Одним из условий ее начала, наряду с окончанием работ 4-7 и 5-7 является выполнение работы 5-6 (через зависимость 6-7).

Расчет временных параметров рассматриваемого комплекса работ и построение сетевого графика осуществляется в определенной последовательности. Пример расчета приведен для n=11.

На первом этапе вычисляем ранние и поздние сроки наступления всех событий T^Pi и T^П_i: на сетевом графике (рисунок 2.2) выделим в каждом кружке, обозначающем событие, три сектора для фиксации его номера и результатов вычислений. Над стрелками графика, обозначающими работы,

Рисунок 2.1 - Сетевая модель организации механосборочного производства

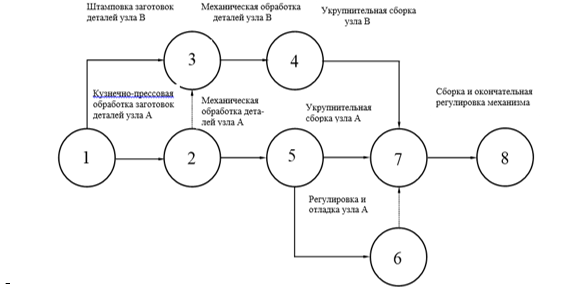
Рисунок 2.2 - Сетевой график организации механосборочного производства отметим числовые значения их продолжительностей, вычисленные с учетом варианта задания;

- примем для исходного события T^Pi = T₁, т.е. заданному сроку наступления. На рис. 2.2 принято T₁ = 0, что записано в левом секторе исходного события

- отметим меткой все работы, выходящие из исходного события (в нашем случае это работы 1-2 и 1-3);

- найдем событие j, для которого все входящие работы отмечены, а T^Pj не найден (в нашем случае это событие 2);

- вычислим T^Pj по формуле:

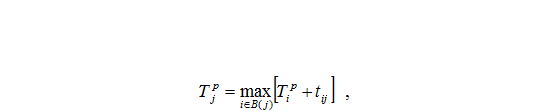
где B_(j) – множество событий i, соединенных с j работами i-j.

В нашем примере:

- отметим меткой все работы, выходящие из события j (в нашем примере из события 2) и вычислим ранние сроки свершения

- событий 3 и 5:

T^P₂=0+33=33 ;

T^P₃ = max[0+11; 33+0] = 33 ;

T^P₅ = 33 + 165 = 198 ;

и т.д. до завершающего события:

T^P₄=33+22=55;

T^P₆=198+11=209;

T^P₇=max[55+132;198+22; 209+0] = 220;

T^P₈=220+11=231;

- поздний срок наступления завершающего события равен раннему сроку его наступления, если нормативный срок не задан, и значению нормативного срока, если последний задан. В нашем случае нормативный срок наступления завершающего события задан и равен 220 часам;

- отметим второй меткой все работы, входящие в завершающее событие. В нашем случае это работа 7-8;

- найдем событие i, для которого все выходящие работы отмечены второй меткой, а поздний срок наступления события ТПi еще не найден. В нашем случае это событие 7;

- вычислим ТПi по формуле:

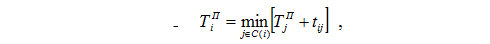
- где С( i ) - множество событий j, соединенных с i работами i-j.

- В нашем примере: ТП7 = 220 - 11 = 209;

- отметим второй меткой все работы, входящие в событие 7 (у нас это работы 4-7, 5-7 и 6-7);

- найдем событие, для которого все выходящие работы отмечены второй меткой, а поздний срок его наступления не найден. В нашем случае это события 4 и 6. Для них:

T^П₄=209-132=77;

T^П₆=209-0=209;

и т.д. до исходного события:

T^П₅=min[209-11; 209-22]=187;

T^П₃=77 - 22 = 55;

T^П₂=min[187 - 165; 55-0] = 22;

T^П₁=min[22-33; 55-11] = -11.;

На втором этапе расчета определим полные и свободные резервы времени всех работ по формулам:

r^П_ij= T^П_j– T^P_i – t_ij

r^СВ_ij= T^P_i– T^P_i – t_ij

Полный резерв представляет собой максимальное время, на которое можно отсрочить начало или увеличить продолжительность работы i-j, не изменяя нормативный срок наступления завершающего события.

Свободный резерв представляет собой максимальное время, на которое можно отсрочить начало или увеличить продолжительность работы i-j при условии, что все события сети наступят в свои ранние сроки.

В нашем случае для работы 7-8:

r^П_7-8= 220 - 220 - 11 =-11; r^CB_7-8= 231-220-11=0;

Аналогично проводим подсчет полных и свободных резервов времени для остальных работ, а результаты записываем в смежных прямоугольниках под стрелками, обозначающими работы (r^П_ij – слева, r^СВ_ij – справа).

Критический путь проходит по работам, имеющим наименьший полный резерв времени (в нашем случае 1-2; 2-5; 5-7; 7-8). Работы критического пути следует отмечать двойной линией.

Результаты расчета временных параметров сетевой модели выявили их несоответствие установленному нормативному сроку. Наличие отрицательных полных резервов свидетельствует об отсутствии такого соответствия и показывает размер расхождения. В этом случае необходимо сократить время выполнения работ критического пути и таким образом привести сетевой график в соответствие с нормативными требованиями.

Указанное сокращения осуществим посредством переброски, таких ресурсов, как часть оборудования и рабочие с некритической работы 4-7, увеличение длительности которой не повлияет на общую продолжительность производства, на критическую работу 2-5 с целью уменьшения её продолжительности на величину, равную размеру полного отрицательного резерва (в рассматриваемом примере на 11 часов).

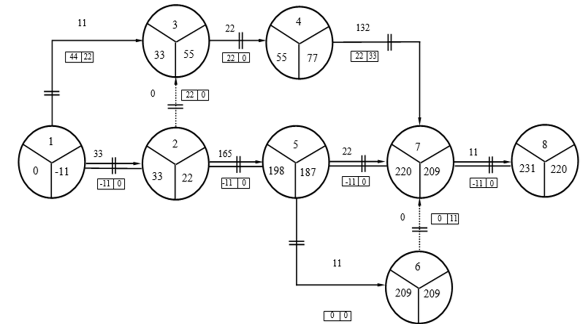
Эффективность принятых мер для приведения расчетного срока окончания работ в соответствие с нормативным подтвердим расчетом оптимизированного сетевого графика (рисунок 2.3).

2.2 Расчет временных параметров сетевого графика в таблице

Задание. Исходные данные, необходимые для расчета временных параметров сетевого графика в таблице, примем в соответствии с оптимизированным графиком (рисунок 2.3).

Табличным методом рассчитать временные параметры сетевого графика и определить критический путь.

Для расчета временных параметров сетевого графика воспользуемся типовой формой таблицы (таблица 2.1), в первую графу которой занесем работы, обозначенные кодами начальных и конечных событий в порядке возрастания их начальных событий.

Рисунок 2.3 - Оптимизированный сетевой график организации механосборочного производства

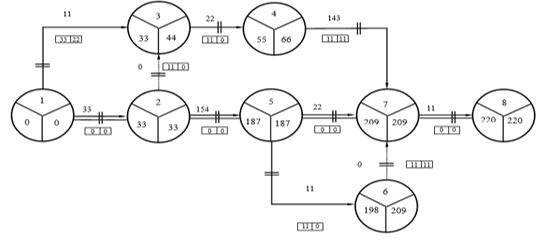
Таблица 2.1 - Расчет временных параметров сетевого графика

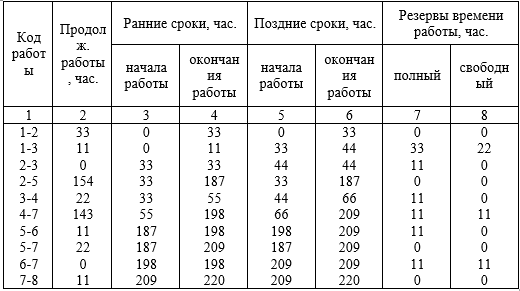
Подсчитаем ранние сроки начала и окончания работ (графы 3 и 4). Очевидно, что ранний срок начала работ 1-2 и 1-3, выходящих из первого события, равен в нашем случае нулю. Раннее окончание этих работ больше раннего начала на величину продолжительности работ.

Ранний срок начала последующих работ равен максимальному из ранних сроков окончания предшествующих работ. Так для работы 2-3

t^рн_2,3 = t^ро_1,2 = 33 часа. Для работы 3-4: t^рн_3,4 = max [t^ро_1,3; t^ро_1,3] = max [11;33] = 33 часа.

И так далее до завершающей работы.

Переходим к расчету поздних сроков начала и окончания работ (графы 5 и 6). В последнюю строку графы 6 занесем нормативный срок окончания всех работ, т.е. срок окончания входящей в завершающее событие работы 7-8 (в нашем случае 220 часов). Далее зафиксируем в графе 5 поздний срок начала указанной завершающей работы, который меньше позднего срока её окончания на величину продолжительности работы:

t^ПН_7,8 = t^ПO_7,8 - t_7,8 = 220-11 = 209 часов.

Затем, двигаясь по графам 5 и 6 снизу вверх, отыскиваем поздний срок окончания очередной вышележащей работы как минимальный среди уже вписанных в графу 5 поздних сроков начала последующих работ с начальными событиями, теми же, что и конечное событие искомой работы. Так для работы 6-7 поздний срок окончания равен позднему сроку начала следующей за ней работы 7-8, т.е. 209 часам. Для работы 2-5:

t^ПО_2,5 = min [t^ПН_5,6; t^ПН_5,7] = min [198;187] = 187 часа.

t^пн_2,5 = t^по_2,5 - t_2,5 = 187 - 154 = 33 часа.

И т.д. до работ, выходящих из исходного события.

Теперь вычислим и занесем в графы 7 и 8 полные и свободные резервы времени работ. Полный резерв вычисляем как разность данных граф 5 и 3. Свободный резерв вычисляем как разность раннего срока начала последующей работы и раннего срока окончания данной работы. Так, для работы 1-2 он равен 33 – 33 = 0, для работы 1-3: 33 – 11 = 22, для работы 2-3: 33 - 33 = 0 и т.д. до завершающей работы. Критически путь, как и при расчете на сетевой модели, пройдет по работам 1-2, 2-5, 5-7 и 7-8 с минимальными полными резервами времени (в нашем случае равными нулю).